
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модель непрерыного канала связиСодержание книги
Поиск на нашем сайте
В непрерывном канале связи входной сигнал x(t) преобразуется из-за наличия помехи в выходной сигнал у(t) (рис. 48). Учитывая, что сигнал имеет случайную природу, он определяется плотностью распределения вероятностей своих значений на входе W(x), а на выходе — W(y).
Количество взаимной информации, связывающей входной и выходной сигналы, соответствует выражению
где Н(у) — энтропия на выходе непрерывного канала; Под пропускной способностью непрерывного канала связи понимают, как и ранее, верхний предел скорости передачи информации, т. е. Пропускная способность непрерывного канала без шума. Для канала без шума Учитывая, что
максимум энтропии получаем для некоторого оптимального распределения
что соответствует нормальному закону. Тогда
где ∆х=∆у — шаг квантования на передающей стороне с учетом требуемой точности воспроизведения непрерывной функции. Пропускная способность непрерывного канала с шумом. Количество взаимной информации, проходящей через такой канал, составляет
Так как
Пропускная способность есть максимум данного выражения, который определяется по распределениям значений функции х(t) на входе непрерывного канала связи. Отметим, что если W(y,x)= W(x)W(y), что соответствует статистически независимым распределениям на входе и на выходе непрерывного канала связи, то С=0. Это означает, что уровень помех в канале достиг такой величины, при которой никакой зависимости между выходным и входным сигналом не остается. Статистическая независимость распределений W(x) и W(y) подтверждает, что сигнал полностью подавлен помехой, полезная информация не передается, т. е. I=0. Это соответствует и нулевой пропускной способности. Заметим, что и в дискретном канале связи при определенном значении вероятности искажения символа пропускная способность снижается до нуля. Очевидно, что такое состояние канала связи является нерабочим и ориентироваться на него не нужно.
2.4.4. Информационный предел избыточности для канала с независимыми ошибками
Процесс передачи данных в реальных системах и сетях реализуется в условиях действия помех, поэтому возникает необходимость построения моделей функционирования системы передачи данных, позволяющих оценить ее вероятностно-временные характеристики. Их удобно находить, исходя из модели передачи данных по дискретному каналу связи, вводя в модель источник ошибок (рис. 49).
Если на вход ДКС поступает некоторая последовательность { х }, а источник ошибок ИО формирует последовательность { е }, то на выходе канала при аддитивности процессов для двоичного кода формируется последовательность В двоичном симметричном канале связи без памяти вероятность искажения любого из передаваемых символов одинакова. Это позволяет применить для описания потока ошибок биномиальный закон распределения. Тогда
где Р — вероятность искажения символа. Отметим, что случай непопадания ошибок на длину кода n возникает с вероятностью Р(0, n)=(1-Р)n, что соответствует n взаимонезависимым событиям прохождения символов. Из биномиального закона нетрудно получить совокупность вероятностей, определяющих возникновение в коде i ошибок и более:
Среднее число ошибок в коде длины n составляет nР. В реальных абонентских каналах связи это число очень мало. Представляет интерес оценить вероятность P(j,n) при Р®0:
При Р≤0,1 находим Р(j,n)=[(nP)j/j|]е-nP. Получаемый при этом закон распределения Пуассона определяется одним параметром nР, что облегчает аналитический расчет вероятностей. Зная модель потока ошибок и избыточность передаваемого кода, можно найти вероятность ошибки в приеме некоторого сообщения у0i. Как было выше показано,
Вероятность перехода сообщения x0j в сообщение у0i назовем вероятностью трансформации сообщения, т. е. Если принятое сообщение соответствует переданному, то это событие можно оценить вероятностью прохождения Р пр, т. е. Пусть через дискретный канал связи передается код, обладающий кодовым расстоянием d, исправляющий s и обнаруживающий r ошибок. Если число ошибок, возникших в коде длины n, не превышает его корректирующей способности, то происходит правильная передача сообщения. Отсюда вероятность прохождения
Используя закон распределения Пуассона, получим
Вероятность ошибки
Очевидно, что с увеличением числа исправляемых ошибок вероятность прохождения увеличивается, а вероятность ошибки уменьшается. Для кода, не исправляющего ошибки, вероятность прохождения Р пр =Р(0,n)=е-nP, откуда вероятность ошибки Р0=1-е-nP. При nР Информационный предел избыточности количественно выражается числом контрольных символов, введенных в код для передачи контрольной информации. При максимальной информативности элемента кода, что соответствует равновероятности передаваемых символов и энтропии источника Нmax{Х)=log2К, получим нижнюю границу избыточности
Так как ошибки, приводящие к трансформации сообщения, исправить невозможно, то ограничимся в структуре контрольной информации лишь той, которая необходима для исправления от нуля до s ошибок, т. е. I K= I Kпр- Для канала с независимыми ошибками
где Отсюда, используя формулу энтропии, находим
Примем допущение, что возникновение любой корректируемой ошибки и отсутствие ошибок происходит с равной вероятностью P1=Pj(1-P)n-j, тогда
Учитывая, что совокупность вариантов корректируемых ошибок составляет полную группу событий, получим
Информационный предел избыточности составит
Отсюда
Формула справедлива для кода, исправляющего s ошибок, с числом переходов d=2s+l. Рассмотренный информационный предел получил название предела Хемминга. В частном случае кода, исправляющего одну ошибку, т. е. s=1, d=3, получаем
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 318; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.252.243 (0.007 с.) |


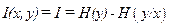 ,
, — условная энтропия, отображающая потери при передаче через непрерывный канал связи.
— условная энтропия, отображающая потери при передаче через непрерывный канал связи.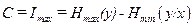 .
. ,
, 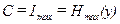
 ,
, ,
, ,
, .
. , то при наличии помех количество передаваемой информации через канал снижается. Обозначим W(x)
, то при наличии помех количество передаваемой информации через канал снижается. Обозначим W(x) 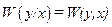 , тогда нетрудно установить, что
, тогда нетрудно установить, что .
.
 { у=хÅе }. Местоположение единиц в { е } указывает ошибки выходной последовательности { у }. При передаче формируются последовательности символов длиной n, отображающие одно или несколько сообщений. Последствия воздействия ошибок на передаваемый код зависят от числа ошибок, попавших на длину кода n. Обозначим вероятность попадания j ошибок на код длины n через P(j,n). Эта вероятность может быть найдена при экспериментальном исследовании путем моделирования, а также на основе аналитических расчетов. Модель дискретного симметричного канала связи позволяет оценить эту вероятность аналитическим путем для отдельных достаточно простых описаний потоков ошибок.
{ у=хÅе }. Местоположение единиц в { е } указывает ошибки выходной последовательности { у }. При передаче формируются последовательности символов длиной n, отображающие одно или несколько сообщений. Последствия воздействия ошибок на передаваемый код зависят от числа ошибок, попавших на длину кода n. Обозначим вероятность попадания j ошибок на код длины n через P(j,n). Эта вероятность может быть найдена при экспериментальном исследовании путем моделирования, а также на основе аналитических расчетов. Модель дискретного симметричного канала связи позволяет оценить эту вероятность аналитическим путем для отдельных достаточно простых описаний потоков ошибок. ,
,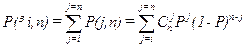 .
.
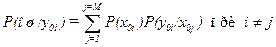 .
. .
. . В реальном канале связи может возникать ситуация, когда принятое сообщение не может быть отождествлено ни с одним из передаваемых. Этот исход получил название «защитного отказа». Он возникает при обнаружении ошибок. Обозначим вероятность защитного отказа Р зо тогда Р пр =1-Р0, где Р0 — вероятность ошибки, Р0 = Р зо + Р тр.
. В реальном канале связи может возникать ситуация, когда принятое сообщение не может быть отождествлено ни с одним из передаваемых. Этот исход получил название «защитного отказа». Он возникает при обнаружении ошибок. Обозначим вероятность защитного отказа Р зо тогда Р пр =1-Р0, где Р0 — вероятность ошибки, Р0 = Р зо + Р тр.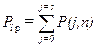 .
.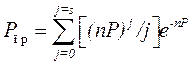
 , следовательно,
, следовательно,
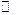 1, используя разложение в ряд Тейлора, получим
1, используя разложение в ряд Тейлора, получим 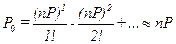 , т. е. вероятность ошибки равна среднему числу ошибок, возникающих на длине кода п. Отсюда следует, что при отсутствии избыточности получить малую вероятность ошибки можно лишь при очень малых значениях nР. С увеличением вероятности искажения символов необходимо ввести избыточность в передаваемый код. При введении избыточности улучшаются обнаруживающие, а при определенном ее уровне и исправляющие свойства кода. Избыточность в коде проявляется в виде контрольной информации Iк, компенсирующей потери информации в обобщенном дискретном канале связи
, т. е. вероятность ошибки равна среднему числу ошибок, возникающих на длине кода п. Отсюда следует, что при отсутствии избыточности получить малую вероятность ошибки можно лишь при очень малых значениях nР. С увеличением вероятности искажения символов необходимо ввести избыточность в передаваемый код. При введении избыточности улучшаются обнаруживающие, а при определенном ее уровне и исправляющие свойства кода. Избыточность в коде проявляется в виде контрольной информации Iк, компенсирующей потери информации в обобщенном дискретном канале связи 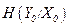 . Можно предположить, что количество контрольной информации и способ ее применения зависят от свойств потока ошибок в канале связи. Минимально необходимая избыточность, компенсирующая ошибки в заданном типе канала связи, получила название информационного предела избыточности.
. Можно предположить, что количество контрольной информации и способ ее применения зависят от свойств потока ошибок в канале связи. Минимально необходимая избыточность, компенсирующая ошибки в заданном типе канала связи, получила название информационного предела избыточности.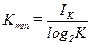 1, где Kmin — минимальное число контрольных символов, определяемое информационным пределом избыточности. Найдем это значение для двоичного дискретного симметричного канала связи с независимыми ошибками. Пусть для передачи сообщений используется двоичный корректирующий код, для которого d=2s+1, r=s, т. е. все обнаруживаемые кодом ошибки исправляются. Тогда возможны два исхода: прохождение сообщения с вероятностью Р пр и трансформация сообщения с вероятностью P тр. Эти исходы должны описывать составляющие контрольной информации, поэтому I K= I Kпр+ I Ктр. Количество контрольной информации найдем с использованием функции энтропии. Исход в приеме сообщений зависит от числа ошибок j, попадающих на длину кода n, т. е. от вероятности Р(j,n). Правильный прием сообщения имеет место, если число ошибок, возникающих на длине кода n, находится в пределах от 0 до s. Трансформация сообщения возможна при числе ошибок от s+l до n. Отсюда находим
1, где Kmin — минимальное число контрольных символов, определяемое информационным пределом избыточности. Найдем это значение для двоичного дискретного симметричного канала связи с независимыми ошибками. Пусть для передачи сообщений используется двоичный корректирующий код, для которого d=2s+1, r=s, т. е. все обнаруживаемые кодом ошибки исправляются. Тогда возможны два исхода: прохождение сообщения с вероятностью Р пр и трансформация сообщения с вероятностью P тр. Эти исходы должны описывать составляющие контрольной информации, поэтому I K= I Kпр+ I Ктр. Количество контрольной информации найдем с использованием функции энтропии. Исход в приеме сообщений зависит от числа ошибок j, попадающих на длину кода n, т. е. от вероятности Р(j,n). Правильный прием сообщения имеет место, если число ошибок, возникающих на длине кода n, находится в пределах от 0 до s. Трансформация сообщения возможна при числе ошибок от s+l до n. Отсюда находим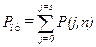 ;
;  .
. ,
, — число сочетаний из n по i.
— число сочетаний из n по i.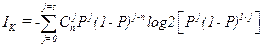 .
.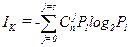 .
. . Отсюда
. Отсюда
 . Если корректирующий код строится для числа передаваемых сообщений М=2m, где m — число информационных элементов в коде, то количество контрольных элементов
. Если корректирующий код строится для числа передаваемых сообщений М=2m, где m — число информационных элементов в коде, то количество контрольных элементов .
. ;. Общее число элементов в коде n=m+k, т. е, k=m-n. Тогда
;. Общее число элементов в коде n=m+k, т. е, k=m-n. Тогда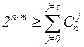 ;
;  .
.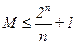 . Таким образом, модель дискретного канала связи в определенной степени задает и модель потока ошибок. Зная модель потока ошибок и свойства дискретного канала связи, можно найти информационный предел избыточности и в соответствии с ним построить код, исправляющий ошибки. Рассмотренная модель независимых ошибок имеет ограниченное применение и справедлива для некоммутируемых телефонных каналов абонентской сети.
. Таким образом, модель дискретного канала связи в определенной степени задает и модель потока ошибок. Зная модель потока ошибок и свойства дискретного канала связи, можно найти информационный предел избыточности и в соответствии с ним построить код, исправляющий ошибки. Рассмотренная модель независимых ошибок имеет ограниченное применение и справедлива для некоммутируемых телефонных каналов абонентской сети.


