
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Моделирование случайных воздействий на системыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте При моделировании системы S методом имитационного моделирования, в частности методом статистического моделирования на ЭВМ, существенное внимание уделяется учету случайных факторов и воздействий на систему. Для их формализации используются случайные события, дискретные и непрерывные величины, векторы, процессы. Формирование на ЭВМ реализаций случайных объектов любой природы из перечисленных сводится к генерации и преобразованию последовательностей случайных чисел. Вопросы генерации базовых последовательностей псевдослучайных чисел {хi}, имеющих равномерное распределение в интервале (0, 1), были рассмотрены во втором вопросе, поэтому остановимся на вопросах преобразования последовательностей случайных чисел {хi} в последовательность {уi} для имитации воздействий на моделируемую систему S. Эти задачи очень важны в практике имитационного моделирования систем на ЭВМ, так как существенное количество операций, а значит, и временных ресурсов ЭВМ расходуется на действия со случайными числами. Таким образом, наличие эффективных методов, алгоритмов и программ формирования, необходимых для моделирования конкретных систем последовательностей случайных чисел {уi}, во многом определяет возможности практического использования машинной имитации для исследования и проектирования систем. Моделирование случайных событий. Простейшими случайными объектами при статистическом моделировании систем являются случайные события. Рассмотрим особенности их моделирования. Пусть имеются случайные числа хi, т.е. возможные значения случайной величины ξ, равномерно распределенной в интервале (0, 1). Необходимо реализовать случайное событие А, наступающее с заданной вероятностью р. Определим А как событие, состоящее в том, что выбранное значение xi случайной величины ξ удовлетворяет неравенству хi ≤ р. Тогда вероятность события А будет Р(А) = Процедура моделирования в этом случае состоит в выборе значений хi и сравнении их с р. При этом, если условие хi ≤ р выполняется, исходом испытания является событие А. Таким же образом можно рассмотреть группу событий. Пусть A1, А2, …, АS – полная группа событий, наступающих с вероятностями p1, р2, …, рS соответственно. Определим Аm как событие, состоящее в том, что выбранное значение хi случайной величины ξ удовлетворяет неравенству lm-1 < xi ≤ lm, где lr = Тогда
Процедура моделирования испытаний в этом случае состоит в последовательном сравнении случайных чисел хi со значениями lr. Исходом испытания оказывается событие Аm, если выполняется условие lm-1 < xi ≤ lm. Эту процедуру называют определением исхода испытания по жребию в соответствии с вероятностями p1, p2, …, pS. При моделировании систем часто необходимо осуществить такие испытания, при которых искомый результат является сложным событием, зависящим от двух (и более) простых событий. Пусть, например, независимые события А и В имеют вероятности наступления рA и рB. Возможными исходами совместных испытаний в этом случае будут события АВ, Для моделирования совместных испытаний можно использовать два варианта процедуры: 1) последовательную проверку условия хi ≤ р; 2) определение одного из исходов АВ, Первый вариант требует двух чисел хi и сравнений для проверки условия хi ≤ р. При втором варианте можно обойтись одним числом xi, но сравнений может потребоваться больше. С точки зрения удобства построения моделирующего алгоритма и экономии количества операций и памяти ЭВМ более предпочтителен первый вариант. Рассмотрим теперь случай, когда события А и В являются зависимыми и наступают с вероятностями р A и рB. Обозначим через Р (В/А) условную вероятность наступления события В при условии, что событие А произошло. При этом считаем, что условная вероятность Р(В/А) задана. Рассмотрим один из вариантов построения модели. Из последовательности случайных чисел {хi} извлекается очередное число хm и проверяется справедливость неравенства хm < рA. Если это неравенство справедливо, то наступило событие А. Для испытания, связанного с событием В, используется вероятность Р (В/А). Из совокупности чисел {хi} берется очередное число xm+1 и проверяется условие хm+1≤Р(В/А). В зависимости от того, выполняется или нет это неравенство, исходом испытания являются АВ или А Если неравенство хm < рA не выполняется, то наступило событие
Выберем из совокупности {хi} число xm+1 и проверим справедливость неравенства xm+1 ≤ P(B/ В зависимости от того, выполняется оно или нет, получим исходы испытания Рассмотрим особенности моделирования на ЭВМ марковских цепей, служащих, например, для формализации процессов в P -схемах. Простая однородная марковская цепь определяется матрицей переходов
где pij – вероятность перехода из состояния zi в состояние zj. Матрица переходов Р полностью описывает марковский процесс. Такая матрица является стохастической, т.е. сумма элементов каждой строки равна единице:
Обозначим через pi(n), i= Используя событийный подход, можно подойти к моделированию марковской цепи следующим образом. Пусть возможными исходами испытаний являются события Al, А2,.., Ak. Вероятность pij – это условная вероятность наступления события Aj в данном испытании при условии, что исходом предыдущего испытания было событие Аi. Моделирование такой цепи Маркова состоит в последовательном выборе событий Аj по жребию с вероятностями pij. Сначала выбирается начальное состояние z0, задаваемое начальными вероятностями р1(0), p2(0), …, pk(0). Для этого из последовательности чисел {xi} выбирается число хm и сравнивается с lr из (4.17), где в качестве рi используются значения р1(0), p2(0), …, pk(0). Таким образом выбирается номер m0, для которого оказывается справедливым неравенство (4.17). Тогда начальным событием данной реализации цепи будет событие р1(0) = p2(0) = … = pk(0)= 1/k. Аналогично можно построить и более сложные алгоритмы, например для моделирования неоднородных марковских цепей. Рассмотренные способы моделирования реализаций случайных объектов дают общее представление о наиболее типичных процедурах формирования реализаций в моделях процессов функционирования стохастических систем, но не исчерпывают всех приемов, используемых в практике статистического моделирования на ЭВМ. Для формирования возможных значений случайных величин с заданным законом распределения исходным материалом служат базовые последовательности случайных чисел {хi}, имеющие равномерное распределение в интервале (0, 1). Другими словами, случайные числа хi как возможные значения случайной величины ξ, имеющей равномерное распределение в интервале (0, 1), могут быть преобразованы в возможные значения уj случайной величины η, закон распределения которой задан. Моделирование дискретных случайных величин. Рассмотрим особенности преобразования для случая получения дискретных случайных величин. Дискретная случайная величина η принимает значения у1 ≤ у2 ≤...≤ уj ≤... с вероятностями pl, р2,..., рj,..., составляющими дифференциальное распределение вероятностей y у1 y2 …yj … Р(η = y) p1 p2 …pj … При этом интегральная функция распределения
Для получения дискретных случайных величин можно использовать метод обратной функции. Если ξ – равномерно распределенная на интервале (0, 1) случайная величина, то искомая случайная величина η получается с помощью преобразования
где Алгоритм вычисления по сводится к выполнению следующих действий: если х1 < р, то η = y1, иначе если х2 < р1 + р2, то η = у2, иначе, ……………………………………….. если хj < …………………………………….. При счете по данному алгоритму среднее число циклов сравнения Моделирование непрерывных случайных величин. Рассмотрим особенности генерации на ЭВМ непрерывных случайных величин. Непрерывная случайная величина η задана интегральной функцией распределения
где fη(у) – плотность вероятностей. Для получения непрерывных случайных величин с заданным законом распределения, как и для дискретных величин, можно воспользоваться методом обратной функции. Взаимно однозначная монотонная функция η = F-1η (ξ), полученная решением относительно η уравнения Fη(y) = ξ, преобразует равномерно распределенную на интервале (0, 1) величину ξ в η с требуемой плотностью fη(у). Действительно, если случайная величина η имеет плотность распределения fη(у), то распределение случайной величины
является равномерным в интервале (0, 1). На основании этого можно сделать следующий вывод. Чтобы получить число, принадлежащее последовательности случайных чисел {yj}, имеющих функцию плотности fη(у), необходимо разрешить относительно уj уравнение
Но этот способ получения случайных чисел с заданным законом распределения имеет ограниченную сферу применения в практике моделирования систем на ЭВМ, что объясняется следующими обстоятельствами: 1) для многих законов распределения, встречающихся в практических задачах моделирования, интеграл 2) даже для случаев, когда интеграл Поэтому в практике моделирования систем часто пользуются приближенными способами преобразования случайных чисел, которые можно классифицировать следующим образом: а) универсальные способы, с помощью которых можно получать случайные числа с законом распределения любого вида; б) неуниверсальные способы, пригодные для получения случайных чисел с конкретным законом распределения. Рассмотрим приближенный универсальный способ получения случайных чисел, основанный на кусочной аппроксимации функции плотности. Пусть требуется получить последовательность случайных чисел {yj} с функцией плотности fη(у), возможные значения которой лежат в интервале (а, b). Представим fη(у) в виде кусочно-постоянной функции, т.е. разобьем интервал (а, b) на m интервалов, как это показано на рис. 4.14, и будем считать fη(у) на каждом интервале постоянной. Тогда случайную величину η можно представить в виде η=ak+ηk*, где ak – абсцисса левой границы k -гo интервала; ηk* – случайная величина, возможные значения которой располагаются равномерно внутри k -гo интервала, т.е. на каждом участке ak-ak+1 величина ηk* считается распределенной равномерно. Чтобы аппроксимировать fη(у) наиболее удобным для практических целей способом, целесообразно разбить (а, b) на интервалы так, чтобы вероятность попадания случайной величины η в любой интервал (ak, ak+1) была постоянной, т.е. не зависела от номера интервала k. Таким образом, для вычисления ak воспользуемся следующим соотношением:
Алгоритм машинной реализации этого способа получения случайных чисел сводится к последовательному выполнению следующих действий: 1) генерируется случайное равномерно распределенное число xi из интервала (0, 1); 2) с помощью этого числа случайным образом выбирается интервал (ak, аk+1); 3) генерируется число хi+1 и масштабируется с целью приведения его к интервалу (аk, аk+1), т.е. домножается на коэффициент (аk+1 - аk)хi+1; 4) вычисляется случайное число yj = аk + (ak+1 - аk)xi+1 с требуемым законом распределения. Достоинства этого приближенного способа преобразования случайных чисел: при реализации на ЭВМ требуется небольшое количество операций для получения каждого случайного числа, так как операция масштабирования вычисления интеграла
|
||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 564; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

 = p. Противоположное событие
= p. Противоположное событие  состоит в том, что хi > р. Тогда Р(
состоит в том, что хi > р. Тогда Р( .
.
 В, А
В, А  ,
,  с вероятностями рAрB, (1-pA)pB, pA(1-pB), (1-pA)(1-pB).
с вероятностями рAрB, (1-pA)pB, pA(1-pB), (1-pA)(1-pB).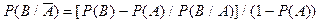 .
. ).
).
 .
. , вероятности того, что система будет находиться в состоянии zi после n переходов. По определению,
, вероятности того, что система будет находиться в состоянии zi после n переходов. По определению, 
 . Затем выбирается следующее случайное число хm+1, которое сравнивается с lr где в качестве pi используются рm0j. Определяется номер m1, и следующим событием данной реализации цепи будет событие Am1 и т.д. Очевидно, что каждый номер mi определяет не только очередное событие Аmi формируемой реализации, но и распределение вероятностей рmi1, рmi2, …, рmik для выбора очередного номера mi+1, причем для эргодических марковских цепей влияние начальных вероятностей быстро уменьшается с ростом номера испытаний. Эргодическим называется всякий марковский процесс, для которого предельное распределение вероятностей pi (n), i =
. Затем выбирается следующее случайное число хm+1, которое сравнивается с lr где в качестве pi используются рm0j. Определяется номер m1, и следующим событием данной реализации цепи будет событие Am1 и т.д. Очевидно, что каждый номер mi определяет не только очередное событие Аmi формируемой реализации, но и распределение вероятностей рmi1, рmi2, …, рmik для выбора очередного номера mi+1, причем для эргодических марковских цепей влияние начальных вероятностей быстро уменьшается с ростом номера испытаний. Эргодическим называется всякий марковский процесс, для которого предельное распределение вероятностей pi (n), i =  .
.
 – функция, обратная F η.
– функция, обратная F η. , то η = ym, иначе,
, то η = ym, иначе, .
.

 .
.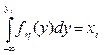 берется в конечном виде, получаются формулы, содержащие действия логарифмирования, извлечения корня и т.д., которые выполняются с помощью стандартных подпрограмм ЭВМ, содержащих много исходных операций (сложения, умножения и т.п.), что также резко увеличивает затраты машинного времени на получение каждого случайного числа.
берется в конечном виде, получаются формулы, содержащие действия логарифмирования, извлечения корня и т.д., которые выполняются с помощью стандартных подпрограмм ЭВМ, содержащих много исходных операций (сложения, умножения и т.п.), что также резко увеличивает затраты машинного времени на получение каждого случайного числа. .
.


