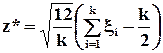Моделирование непрерывных случайных величин

В качестве базовых используются случайные величины с равномерным законом распределения. Базовый датчик (генератор случайных величин) выдает независимые случайные величины, равномерно распределенные в диапазоне [0¸1]. Для получения случайной величины, равномерно распределенной в интервале [a, b] можно использовать следующий прием:

z = x(b – a) + a (7.2)

где x – случайная величина, равномерно распределенная в интервале [0, 1].

При этом (b – a) является коэффициентом масштабирования, a – величиной сдвига.

Для получения случайной величины, имеющей экспоненциальное (показательное) распределение используются зависимости:

где l - параметр распределения.

Таким образом, получая значение x с помощью датчика равномерно распределенных случайных чисел на интервале [0,1], можно получить значения z, т.е. экспоненциально распределенной случайной величины.

Для получения нормального распределение центрированной (m=0) и нормированной (s=1) случайной величины можно выполнить следующее преобразование:

где x_i – отсчеты базовой случайной величины, m – математическое ожидание; s - дисперсия.

Наиболее удобной для расчетов данная формула становится при k = 12.

Для получения нормально распределенной величины с произвольными значениями m и s, пользуются дополнительным преобразованием:

z = sz* + m

где z* – центрированная и нормированная величина.

Следует отметить, что согласно литературным данным приведенная зависимость дает достаточно точные результаты уже для k = 4.

 

Моделирование потоков событий

Моделирование потока событий сводится к моделированию моментов времени, в которые они происходят.

Если интервалы времени между событиями являются равномерно распределенными случайными величинами, то моменты наступления событий можно определить так:

t_i+1 = t_i + z

где z – равномерно распределенная в необходимом интервале случайная величина.

Для простейшего потока событий, обладающего свойствами ординарности, стационарности и отсутствия последействия, интервалы времени между событиями представляют собой непрерывные случайные величины, распределенные по экспоненциальному закону.

Следовательно, моменты наступления событий в простейшем потоке могут моделироваться с использованием выражения:

где l - интенсивность потока: x – случайная величина, равномерно распределенная в интервале [0, 1].

Потоки событий Эрланга являются примерами потоков с ограниченным последействием. Данные потоки образуются путем закономерного просеивания простейшего потока. Например, при получении потока Эрланга k -го порядка, просеивание сводится к выбору из исходного простейшего (базового) потока каждого k -го события. Это эквивалентно образованию длины интервала потока Эрланга в виде суммы k смежных интервалов

При моделировании интервалы между событиями в полученном просеиванием потоке Эрланга обычно нормируют коэффициентом k в целях коррекции масштаба времени:

t_ЭН = t_Э/k

 

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача 15

Получить десять значений нормально распределенной случайной величины, имеющей математическое ожидание, равное 2 и дисперсию, равную 1. Описать процедуру получения искомых чисел. Результаты представить в таблице.

Решение

Для получения нормально распределенной величины с произвольными значениями дисперсии и математического ожидания используем выражение:

z = sz* + m

где z* – центрированная и нормированная величина; m – математическое ожидание; s - дисперсия.

Для нашего случая z = z* + 2

Центрированную и нормированную случайную величину можно получить по зависимости:

где x_i – отсчеты базовой случайной величины.

Воспользуемся данной зависимостью при k = 6. Тогда

Окончательно выражение для получения нормально распределенной случайной величины с заданными характеристиками примет вид:

Для получения каждого из искомых чисел следует сгенерировать шесть случайных чисел, равномерно распределенных в диапазоне [0¸1], а затем воспользоваться полученным выражением. Результаты моделирования, полученные с использованием процессора электронных таблиц Excel и округленные до трех значащих цифр, приведены в таблице. Для генерации базовых случайных чисел использовалась функция СЛЧИС.

1,78

2,56

1.44

1,92

2,07

2,13

2,23

1,16

2,71

1,66

 

Задача 16

Получить десять значений моментов времени, в которые происходят события в потоке событий, если интервалы времени между ними являются равномерно распределенными случайными величинами. Известно, что за 10 с происходит в среднем 5 событий. Описать процедуру получения искомых значений. Результаты представить в таблице.

Решение

Согласно исходным данным одно событие происходит в среднем каждые 2 с. Поскольку математическое ожидание базовой случайной величины равно 0,5 то в нашем случае следует брать случайную величину, равномерно распределенную в интервале [0, 4].

Поэтому для получения искомых значений нужно воспользоваться зависимостью:

t_i+1 = t_i + 4x

Результаты моделирования, полученные с использованием процессора электронных таблиц Excel и округленные до одной сотой, приведены в таблице. Для генерации базовых случайных чисел использовалась функция СЛЧИС.

0,89

1,96

4,88

5,85

6,33

8,75

10,56

10,62

12,55

15,11