
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модель дискретного канала связиСодержание книги
Поиск на нашем сайте
Дискретный канал связи (ДКС) имеет на входе множество символов кода X с энтропией источника Н(Х), а на выходе — множество символов Y с энтропией H(Y) (рис. 42).
Если формируемые символы из множества X и выявляемые из множества Y расположить в узлах графа, соединив эти узлы дугами, отображающими вероятности перехода одного символа в другой, то получим модель дискретного канала связи, представленную на рис. 43. Множество символов X конечно и определяется основанием системы счисления кода Кх на входе канала. Система счисления по выявляемым символам также конечна и составляет Ку. Вероятности переходов, связывающих входные и выходные символы, могут быть записаны в виде матрицы
В этой матрице i-й столбец определяет вероятность выявления выходе дискретного канала связи символа уi. Вероятности, рас положенные на главной диагонали, называются вероятностями прохождения символов, остальные вероятности есть вероятность трансформации. Анализ модели дискретного канала связи возможен, если известна статистика появления символов на входе канала. Тогда может быть определена энтропия Н(Х). Если известна статистика символов на выходе канала, то нетрудно установить энтропию Н(Y). Потери информации могут быть вызваны действием помех, которые отображаются в дискретном канале в виде некоторого потока ошибок. Поток ошибок задается с помощью определенной модели ошибок, на основании которой может быть установлена матрица Р. Зная эту матрицу, находят условную энтропию По основанию системы счисления коды на входе ДКС различают двоичные, троичные, четверичные каналы связи и другие. По соотношению системы счисления на выходе и на входе ДКС выделяют каналы со стиранием, если Ку>Кх, и каналы без стирания, если Ку=Кх. По наличию зависимости вероятности переходов символов в ДКС от времени выделяют нестационарные каналы, для которых такая зависимость существует, и стационарные каналы, где вероятности переходов постоянны. Нестационарные каналы могут быть классифицированы по наличию зависимости вероятности переходов от предшествующих значений. Выделяют дискретные каналы с памятью, в которых такая зависимость имеет место, и дискретные каналы без памяти, где этой зависимости не существует. При определенных соотношениях между вероятностями переходов, входящих в матрицу Р, выделяют: симметричные каналы по входу, для которых вероятности, входящие в строку матрицы. являются перестановками одних и тех же чисел; симметричные каналы по выходу, для которых это относится к вероятностям, входящим в столбцы; симметричные каналы по входу и по выходу при соблюдении обоих условий. На основе представленной классификации матрица двоичного симметричного канала имеет вид
где Р — вероятность искажения символа. Соответственно матрица двоичного симметричного канала со стиранием
где Р — вероятность трансформации; 1-Р-q — вероятность прохождения символа; q — вероятность стирания символа. Для граничного случая двоичного симметричного канала без шума матрица переходов имеет вид
Граф К -го канала без шума представлен на рис. 44.
С использованием дискретного канала связи могут быть решены основные проблемы передачи. Для канала без шума — это выбор оптимального кода, который по своим свойствам согласуется с источником, т. е. имеет наименьшую среднюю длину. Для канала с шумом — это выбор кода, который обеспечивает заданную вероятность передачи при максимально возможной скорости. Для решения этих проблем рассмотрим основные характеристики ДКС. Основной характеристикой дискретного канала является пропускная способность, Под которой понимают верхний предел количества информации, которую можно передать через канал связи, отображаемый заданной моделью. Оценим пропускную способность дискретного канала связи. Количество взаимной информации, связывающей множества символов X, Y, составит Раскроем данное выражение для отдельных вариантов дискретного канала связи. Пропускная способность дискретного канала связи без шума. При отсутствии шума потерь информации в канале нет, а поэтому Таким образом, пропускная способность дискретного канала без шума зависит только от основания кода. Чем оно больше, тем выше информативное» каждого символа, тем больше пропускная способность. Пропускная способность измеряется в двоичных единицах на символ и не связана в данном представлении со временем. При переходе от двоичного кода к четвертичному пропускная способность ДКС без шума увеличивается в два раза. Пропускная способность дискретного симметричного канала связи с шумом. Рассмотрим канал без стирания, для которого Кx=Кy=К. При наличии шума в ДКС входной символ xj переходит в символ уi, с вероятностью
Принимая, что на входе ДКС символы равновероятны, т. е.
Минимум условной энтропии достигается соответствующим выбором порога срабатывания приемной схемы, при котором обеспечивается минимальное значение вероятности трансформации Р. Отсюда пропускная способность
Видно, что она увеличивается с ростом основания кода и с уменьшением вероятности трансформации символа. В случае двоичного симметричного канала с шумом пропускная способность может быть найдена при К=2, т. е. С=1+(1-P)log2(1-P)+Plog2P. Зависимость пропускной способности двоичного симметричного канала от вероятности искажения символа представлена на рис. 46. При Р=0 получим С=1. С ростом вероятности искажения до 0,5 пропускная способность падает до нуля.
Рабочий диапазон дискретного канала соответствует вероятности Р<0,1. При этом пропускная способность близка к единице. Пропускная способность двоичного симметричного канала со стиранием. Если на входе двоичного канала имеют место символы х1, х2, то при наличии стирания на выходе канала возникают символы у1, у2 и символы стирания у3. Символ стирания формируется при наличии в приемном устройстве специальной зоны стирания, попадание в которую означает возникновение символа неопределенности (стирания). Введение зоны стирания в приемное устройство позволяет снизить вероятность трансформации символа Р за счет появления вероятности стирания символа q (рис. 47). Тогда вероятность прохождения символа составляет l-P-q. Пропускная способность
где P(yi) — вероятность возникновения на выходе дискретного канала символа уi. Найдем вероятности возникновения символов на выходе при Условии, что символы на входе равновероятны, тогда
Отсюда
Соответственно условная энтропия
Отсюда пропускная способность
Опыт применения канала со стиранием показал, что введение зоны стирания эффективно лишь при наличии помех. Тогда удается получить P«q и повысить пропускную способность канала связи. В общем случае в условиях действия помех повышение пропускной способности дискретного канала достигается за счет равновероятности символов на выходе и снижения вероятности искажения символа. В случае симметричного канала связи равновероятность символов на выходе означает необходимость равновероятности символов на входе канала. Это условие соответствует полученному ранее требованию построения оптимального кода. Снижение вероятности искажения символа в дискретном канале зависит от конструирования приемной схемы на физическом уровне. Закон распределения помехи на выходе непрерывного канала связи позволяет найти оптимальное значение порога срабатывания приемной схемы и исходя из него оценить и минимизировать вероятность искажения символов. Таким образом, на основании модели дискретного канала связи можно установить верхний предел скорости передачи информации и согласовать производительность источника с пропускной способностью канала связи. Условная энтропия
|
||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 515; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.012 с.) |


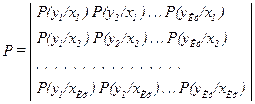
 , которая, как выше показано, отображает потери информации при прохождении ее по каналу связи. В данном случае
, которая, как выше показано, отображает потери информации при прохождении ее по каналу связи. В данном случае 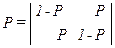



 . Пропускная способность
. Пропускная способность  .
. , тогда C=Imax=Hmax(Y). Как известно, максимум энтропии для дискретных событий достигается при их равновероятности. Учитывая, что на выходе канала связи может появиться Ку символов, получим, что
, тогда C=Imax=Hmax(Y). Как известно, максимум энтропии для дискретных событий достигается при их равновероятности. Учитывая, что на выходе канала связи может появиться Ку символов, получим, что 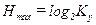 . Отсюда C=log2Kу.
. Отсюда C=log2Kу. . Вероятность трансформации символа составит
. Вероятность трансформации символа составит  . Если канал симметричен, то вероятности, входящие в данную сумму, одинаковы, а поэтому
. Если канал симметричен, то вероятности, входящие в данную сумму, одинаковы, а поэтому 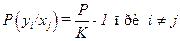 . Вероятность прохождения символа
. Вероятность прохождения символа 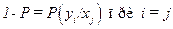 (рис. 45). Пропускная способность рассматриваемого канала
(рис. 45). Пропускная способность рассматриваемого канала  .
.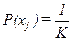 , находим
, находим
 .
.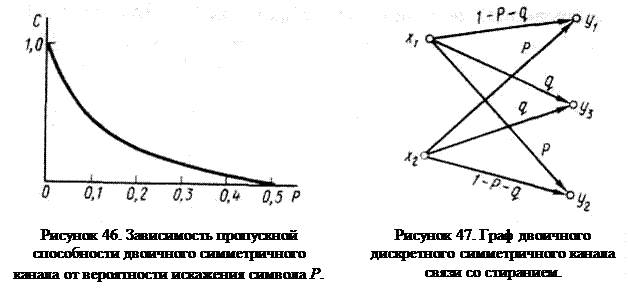
 . При наличии символа стирания стремление к равновероятности символов на выходе канала не имеет смысла, поэтому энтропия на выходе H(Y) определяется как
. При наличии символа стирания стремление к равновероятности символов на выходе канала не имеет смысла, поэтому энтропия на выходе H(Y) определяется как ,
, ,
, ;
; ;
; .
. .
. .
. .
. дает возможность оценить минимально необходимую избыточность, отнесенную к одному символу кода. Это позволяет найти нижний предел избыточности при построении обнаруживающих и корректирующих кодов для каналов связи с шумами. Конкретное значение избыточности устанавливается из требований к вероятностно-временным характеристикам процесса передачи. Эти характеристики могут быть рассчитаны на основе модели функционирования системы передачи данных.
дает возможность оценить минимально необходимую избыточность, отнесенную к одному символу кода. Это позволяет найти нижний предел избыточности при построении обнаруживающих и корректирующих кодов для каналов связи с шумами. Конкретное значение избыточности устанавливается из требований к вероятностно-временным характеристикам процесса передачи. Эти характеристики могут быть рассчитаны на основе модели функционирования системы передачи данных.


