

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Каноническая структура информационной базы
При известной инфологической модели предметной области, наличии вычислительного и информационного графов возникает проблема создания модели накопления данных, в основе которой лежит задача выбора хранимых данных. Пусть совокупность используемых наборов данных N разделена на N1 первичных (входных), N2 промежуточных и N3 выходных наборов данных, т. е. N=NlÈN2ÈN3. Получение наборов данных N3 осуществляется на основе вычислительных алгоритмов и алгоритмов корректировки. Вычислительный алгоритм представляется вычислительной схемой, т. е. подграфом вычислительного графа. Алгоритм корректировки базируется на множестве первичных данных N1. Даже при наличии лишь двух классов алгоритмов возникает задача выбора типа алгоритма в соответствии с запросом пользователя. Если по запросу необходимо получить некоторый набор данных, то в качестве критерия выбора типа алгоритмов можно использовать полное время создания этого набора по данному запросу. При использовании вычислительного алгоритма это время складывается из времени, которое затрачивается на получение входных наборов данных для выбранного вычислительного модуля, и времени вычислений набора данных этим модулем. Для сравнения необходимо найти время, которое затрачивается в случае применения алгоритма корректировки. Корректировка набора целесообразна, если структура данных уже ранее была задана в одном из предыдущих запросов. В качестве дополнительного ограничения при решении задачи выступает объем используемой памяти. Рациональное сочетание вычислительных алгоритмов и алгоритмов корректировки данных позволяет уменьшить суммарное время реализации всех запросов при накоплении данных.
Мифологическая модель предметной области позволяет подойти к решению двух задач: задачи синтеза информационной базы и задачи управления вычислительным процессом. При синтезе информационной базы необходимо установить ее структуру. Представление информации пользователей дает каноническая структура информационной базы, поэтому построение модели накопления данных должно базироваться на синтезе канонической структуры. Это проводится при следующих требованиях: единство инфологической модели для множества предметных областей, обслуживаемых информационной базой; выбор безызбыточного набора информационных элементов и связей между ними; реализация интерфейса пользователя с информационной базой в терминах мифологической додели предметной области; возможность простого перевода понятий канонической структуры в понятия логического и физического уровней представления информационной базы. Решение задачи синтеза канонической структуры информационной базы предполагает
1) выбор и упорядочение ключевых реквизитов для множества бинарных отношений, хранимых в информационной базе;
2) формирование логических записей на основе объединения значений реквизитов;
3) определение множества логических записей и связей между ними на основе критерия минимума суммарного времени работы с наборами данных как в режиме вычислительных алгоритмов, так и в режиме алгоритмов корректировки.
Упорядочение ключевых реквизитов отношений должно базироваться на возможности физической реализации информационной базы. Учитывая, что современные СУБД не могут реализовать n -арные отношения между данными, представим любое отношение в виде совокупности бинарных отношений. Это означает упорядочение реквизитов, входящих в ключ каждого функционального отношения Ф, что можно осуществить на основе построения графа, отображающего (di dj)2, где l¹j; ij=1-N; 1≤r≤N-1. Для этого графа матрица Q, отображающая взаимосвязь между отдельными данными и группами данных, имеет вид

 В общем случае под di, dj можно понимать некоторые обобщенные информационные элементы, представляющие собой элементы данных либо группы, составленные из этих элементов: qij=l, если существует взаимосвязь (в том числе возможна и семантическая) между элементами di, dj qij=0 при отсутствии взаимосвязи. Если строка матрицы Q содержит все нулевые элементы, то этой строкой отображаются входные данные. В информационном графе эти данные соответствуют корневым вершинам. Если столбец матрицы Q содержит все нулевые элементы, то он отображает терминальные, т. е. выходные, данные. На информационном графе эти данные соответствуют концевым вершинам. Остальные информационные элементы, отображаемые строками и столбцами матрицы Q, отнесем к групповым элементам. На информационном графе они располагаются в промежуточных вершинах. Объединение множеств значений реквизитов можно выполнить на основе оценки взаимосвязи групповых элементов с подчиненными им выходными. Тогда для группы конечных вершин (терминальных элементов) выделяется множество групповых висячих вершин dr, drÎD. Для множества dr может быть построена матрица достижимости вида Qr, представляющая собой квадратную матрицу с числом строк и столбцов, соответствующим количеству элементов в выделенном множестве dr. При переходе к логическому уровню представления информационной базы информационные элементы и взаимосвязи между ними упорядочиваются по уровням иерархии. Для этого определим множество предшествования и множество достижимости. Для информационного элемента dj матрицы Q множество предшествования П(dj) определяется из совокупности информационных элементов di соответствующих единичной записи в j -м столбце. Анализируя множество H(dj), устанавливают базовые типы структурных элементов, на основе которых формируются информационные группы. Элементам, для которых П(dj)=Æ, соответствуют промежуточные вершины графа. Из матрицы Q для элемента dj выявляют и множество достижимости этих данных D(dj). Это множество формируется за счет элементов di, которым соответствуют единичные записи в j -й строке матрицы Q. Тогда элементы данных dj принадлежат группе r, т. е. определяются как dj, если В общем случае под di, dj можно понимать некоторые обобщенные информационные элементы, представляющие собой элементы данных либо группы, составленные из этих элементов: qij=l, если существует взаимосвязь (в том числе возможна и семантическая) между элементами di, dj qij=0 при отсутствии взаимосвязи. Если строка матрицы Q содержит все нулевые элементы, то этой строкой отображаются входные данные. В информационном графе эти данные соответствуют корневым вершинам. Если столбец матрицы Q содержит все нулевые элементы, то он отображает терминальные, т. е. выходные, данные. На информационном графе эти данные соответствуют концевым вершинам. Остальные информационные элементы, отображаемые строками и столбцами матрицы Q, отнесем к групповым элементам. На информационном графе они располагаются в промежуточных вершинах. Объединение множеств значений реквизитов можно выполнить на основе оценки взаимосвязи групповых элементов с подчиненными им выходными. Тогда для группы конечных вершин (терминальных элементов) выделяется множество групповых висячих вершин dr, drÎD. Для множества dr может быть построена матрица достижимости вида Qr, представляющая собой квадратную матрицу с числом строк и столбцов, соответствующим количеству элементов в выделенном множестве dr. При переходе к логическому уровню представления информационной базы информационные элементы и взаимосвязи между ними упорядочиваются по уровням иерархии. Для этого определим множество предшествования и множество достижимости. Для информационного элемента dj матрицы Q множество предшествования П(dj) определяется из совокупности информационных элементов di соответствующих единичной записи в j -м столбце. Анализируя множество H(dj), устанавливают базовые типы структурных элементов, на основе которых формируются информационные группы. Элементам, для которых П(dj)=Æ, соответствуют промежуточные вершины графа. Из матрицы Q для элемента dj выявляют и множество достижимости этих данных D(dj). Это множество формируется за счет элементов di, которым соответствуют единичные записи в j -й строке матрицы Q. Тогда элементы данных dj принадлежат группе r, т. е. определяются как dj, если  . На основе этого условия группы итеративно разбиваются по уровням иерархии, начиная с верхнего уровня. Группы самого верхнего уровня называются корневыми группами, поскольку они располагаются в корневых вершинах графа. Группы следующих рангов располагаются в промежуточных вершиных, доступ к которым возможен через корневые группы. Поэтому с помощью корневых групп определяются точки входа к данным информационной базы. Состав информационных элементов, входящих в группу . На основе этого условия группы итеративно разбиваются по уровням иерархии, начиная с верхнего уровня. Группы самого верхнего уровня называются корневыми группами, поскольку они располагаются в корневых вершинах графа. Группы следующих рангов располагаются в промежуточных вершиных, доступ к которым возможен через корневые группы. Поэтому с помощью корневых групп определяются точки входа к данным информационной базы. Состав информационных элементов, входящих в группу  , можно определить, включив в нее элементы di которым соответствуют единичные записи в j -м столбце матрицы Q. Упорядочивая таким способом элементы матрицы Q, получают структурированный граф, в котором возможные точки входа соответствуют групповым элементам первого уровня, конечные вершины — выходным данным. В промежуточных вершинах располагаются групповые элементы различных уровней иерархии. , можно определить, включив в нее элементы di которым соответствуют единичные записи в j -м столбце матрицы Q. Упорядочивая таким способом элементы матрицы Q, получают структурированный граф, в котором возможные точки входа соответствуют групповым элементам первого уровня, конечные вершины — выходным данным. В промежуточных вершинах располагаются групповые элементы различных уровней иерархии.
Выбор ключевых реквизитов
Выделение групповых элементов и состава информационных элементов в группах позволяет с помощью ориентированного графа построить траекторию доступа к каждому информационному элементу группы. Доступ осуществляется через корневую вершину графа. Для построения ключевых реквизитов необходимо проанализировать отношения между групповыми информационными элементами. Поиск информационных элементов в базе осуществляется по требованиям пользователя. Если k- е требование пользователя содержит Dk элементов, выбираемых из общего числа структурных элементов инфологической модели предметной области, то можно построить матрицу смежности sk для информационного требования Dk. Элемент этой матрицы sij=1, если существует связь между элементами di, dj в требовании Dk. На основании элементов  могут быть названы элементы могут быть названы элементы 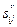 , соответствующие групповым информационным элементам базы. В зависимости от характера групп выделяют , соответствующие групповым информационным элементам базы. В зависимости от характера групп выделяют  , ,  . Этим элементам будут соответствовать простые группы. Если . Этим элементам будут соответствовать простые группы. Если  , ,  , то получим группы — массивы. Для простых групп образуют простой ключ, для групп массивов — составной ключ, включающий в себя основной и вспомогательный ключи. При этом основной ключ определяется терминальным, конечным элементом, входящим в состав группы массива. Выделение основных ключей должно быть неизбыточным, поэтому необходимо установить и устранить дублируемые терминальные конечные элементы данных. , то получим группы — массивы. Для простых групп образуют простой ключ, для групп массивов — составной ключ, включающий в себя основной и вспомогательный ключи. При этом основной ключ определяется терминальным, конечным элементом, входящим в состав группы массива. Выделение основных ключей должно быть неизбыточным, поэтому необходимо установить и устранить дублируемые терминальные конечные элементы данных.
Пусть групповому элементу  , соответствует множество терминальных элементов , соответствует множество терминальных элементов  , а групповому элементу d) — множество терминальных элементов D (d'X Известно, что групповые элементы семантически связаны, если , а групповому элементу d) — множество терминальных элементов D (d'X Известно, что групповые элементы семантически связаны, если 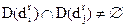 . Соответственно семантическая независимость групповых элементов удовлетворяет условию . Соответственно семантическая независимость групповых элементов удовлетворяет условию 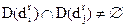 . Если последнее условие выполняется для всех попарно выбираемых групповых элементов данного уровня иерархии, а затем и для всех более высоких уровней, то дублирование отсутствует. Если условие не выполняется, то имеют место дублируемые терминальные, конечные элементы. Устранение дублируемых терминальных элементов достаточно легко осуществляйся, если групповые элементы построены на одном и том же типе отношений. . Если последнее условие выполняется для всех попарно выбираемых групповых элементов данного уровня иерархии, а затем и для всех более высоких уровней, то дублирование отсутствует. Если условие не выполняется, то имеют место дублируемые терминальные, конечные элементы. Устранение дублируемых терминальных элементов достаточно легко осуществляйся, если групповые элементы построены на одном и том же типе отношений.
Пусть групповой элемент  принадлежит уровню иерархии n, а элемент принадлежит уровню иерархии n, а элемент  — уровню иерархии m, причем m<n. При наличии пути на графе из элемента — уровню иерархии m, причем m<n. При наличии пути на графе из элемента  к элементу к элементу  следует убрать дублируемые терминальные элементы из множества следует убрать дублируемые терминальные элементы из множества  . Удаление терминального элемента должно быть отражено и в матрице Q. Это означает, что коэффициент qij=1, показывающий ранее связь между элементами di, dj, становится равным нулю. Если групповые элементы . Удаление терминального элемента должно быть отражено и в матрице Q. Это означает, что коэффициент qij=1, показывающий ранее связь между элементами di, dj, становится равным нулю. Если групповые элементы  , ,  построены на разных типах отношений, то устранение терминальных элементов осуществляется эвристически с использованием той же идеи: расположением терминального элемента на более высоком уровне иерархии и устранением дублируемого элемента на нижнем уровне. Размещение терминальных элементов на более высоких уровнях иерархии в графе обеспечивает уменьшение времени доступа к конечному элементу, так как сокращается путь от корневой вершины до терминального элемента в графе. построены на разных типах отношений, то устранение терминальных элементов осуществляется эвристически с использованием той же идеи: расположением терминального элемента на более высоком уровне иерархии и устранением дублируемого элемента на нижнем уровне. Размещение терминальных элементов на более высоких уровнях иерархии в графе обеспечивает уменьшение времени доступа к конечному элементу, так как сокращается путь от корневой вершины до терминального элемента в графе.
При построении канонической структуры информационной базы необходимо устранить также избыточные связи между групповыми элементами. При наличии таких связей по одному и тому же ключу могут вызываться разные групповые элементы данных, что является недопустимым. Избыточная связь между группами  , ,  может на графе представляться непосредственно дугой (i,j), соединяющей групповые элементы данных, либо путем, включающим в себя ряд дуг. Если избыточной оказывается дуга (i,j), то она легко обнаруживается по матрице Q для элемента qij= 1. Заменяем этот элемент на нулевой, что соответствует устранению избыточной дуги. Если путь, связывающий групповые элементы данных, включает несколько дуг, то необходимо найти матрицу Qk, где к=2,3,...,Nk, Nk — максимальное число групповых элементов данных. Тогда получим квадратную матрицу, элемент которой может на графе представляться непосредственно дугой (i,j), соединяющей групповые элементы данных, либо путем, включающим в себя ряд дуг. Если избыточной оказывается дуга (i,j), то она легко обнаруживается по матрице Q для элемента qij= 1. Заменяем этот элемент на нулевой, что соответствует устранению избыточной дуги. Если путь, связывающий групповые элементы данных, включает несколько дуг, то необходимо найти матрицу Qk, где к=2,3,...,Nk, Nk — максимальное число групповых элементов данных. Тогда получим квадратную матрицу, элемент которой  показывает число путей, ведущих из группы показывает число путей, ведущих из группы  группу группу  . Если в исходной матрице Q элемент qij= 1, а в полученной матрице Qk элемент . Если в исходной матрице Q элемент qij= 1, а в полученной матрице Qk элемент  , то связь является избыточной. Для удаления этой связи заменяем qij= 1 на нулевой элемент. Граф, получаемый после удаления избыточных терминальных элементов и избыточных связей между групповыми элементами данных, определяет каноническую структуру информационной базы. Таким образом, каноническая структура задает логически не избыточную информационную базу. Выделение групповых элементов данных в канонической структуре позволяет объединить множество значений конечных элементов (реквизитов) в логические записи и тем самым упорядочить их в памяти ЭВМ. Структура логических записей и связей между ними должна быть такова, чтобы обеспечить минимум суммарного времени работы с наборами данных как при решении функциональных задач, так и при их корректировке. Поэтому необходимо установить характеристики канонической структуры информационной базы. , то связь является избыточной. Для удаления этой связи заменяем qij= 1 на нулевой элемент. Граф, получаемый после удаления избыточных терминальных элементов и избыточных связей между групповыми элементами данных, определяет каноническую структуру информационной базы. Таким образом, каноническая структура задает логически не избыточную информационную базу. Выделение групповых элементов данных в канонической структуре позволяет объединить множество значений конечных элементов (реквизитов) в логические записи и тем самым упорядочить их в памяти ЭВМ. Структура логических записей и связей между ними должна быть такова, чтобы обеспечить минимум суммарного времени работы с наборами данных как при решении функциональных задач, так и при их корректировке. Поэтому необходимо установить характеристики канонической структуры информационной базы.
Существенными являются длины групповых элементов данных представляющие собой сумму длин терминальных элементов, входящих в данную группу. Для группы  длина группового элемента длина группового элемента  где где  — длина терминального элемента данных. Интегральная оценка длин логических записей может быть произведена на основе вектора — длина терминального элемента данных. Интегральная оценка длин логических записей может быть произведена на основе вектора 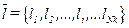 . .
Любая информационная база характеризуется таким параметром, как время доступа пользователя к данным. Однако на этапе создания канонической структуры физическая организация базы данных неизвестна, поэтому реальное время поиска данных не удается определить. Тем не менее, нужно оценить минимальное значение времени обращения к базе данных каш в процессе решения функциональной задачи, так и в процессе корректировки базы.
Для групповых элементов данных в канонической структуре может быть задана матрица
Т= ||ti||, где ti — минимальное время доступа к терминальным элементам di, входящим в группу  . Если функциональная задача решается на основе вычислительного алгоритма aj, то время работы алгоритма с реквизитами di определяется как . Если функциональная задача решается на основе вычислительного алгоритма aj, то время работы алгоритма с реквизитами di определяется как  где где  — время поиска реквизита di при решении задачи на основе алгоритма аj. Значение этого времени зависит от вида обработки реквизита di в выбранном алгоритме (возможна последовательная обработка значений данных либо обработка по ключу). При использовании алгоритмов коррекции корректируются все отношения, которые содержат изменяемый ключевой реквизит и зависимые от него реквизиты. Значение времени работы алгоритма с данными — время поиска реквизита di при решении задачи на основе алгоритма аj. Значение этого времени зависит от вида обработки реквизита di в выбранном алгоритме (возможна последовательная обработка значений данных либо обработка по ключу). При использовании алгоритмов коррекции корректируются все отношения, которые содержат изменяемый ключевой реквизит и зависимые от него реквизиты. Значение времени работы алгоритма с данными  определяется количеством копий, присутствующих в корректируемых реквизитах. На уровне канонической структуры число копий задается количеством экземпляров терминальных элементов, входящих в группу определяется количеством копий, присутствующих в корректируемых реквизитах. На уровне канонической структуры число копий задается количеством экземпляров терминальных элементов, входящих в группу  . Обычно алгоритм коррекции имеет возможность обращаться по ключу к информационным элементам базы данных . Обычно алгоритм коррекции имеет возможность обращаться по ключу к информационным элементам базы данных
 , где , где  , если , если  ; ;  , в противном случае. Методика построения канонической структуры информационной базы практически не меняется в зависимости от того, строится централизованная либо распределенная информационная база. При создании распределенной информационной базы матрица Q раскрывается для каждого пользователя. На графе для каждого пользователя формируются групповые и терминальные элементы данных. Полное множество групповых элементов находится путем пересечения групповых элементов данных отдельных пользователей. Таким образом, каноническую структуру информационной базы можно считать универсальной формой представления мифологической модели предметов, области и безызбыточной формой модели накопления данных. От канонической структуры переходят к логической структуре информационной базы и к физической организации информационных массивов. Каноническая структура является также основой автоматизации основных процессов предпроектного анализа предметной областей пользователей. , в противном случае. Методика построения канонической структуры информационной базы практически не меняется в зависимости от того, строится централизованная либо распределенная информационная база. При создании распределенной информационной базы матрица Q раскрывается для каждого пользователя. На графе для каждого пользователя формируются групповые и терминальные элементы данных. Полное множество групповых элементов находится путем пересечения групповых элементов данных отдельных пользователей. Таким образом, каноническую структуру информационной базы можно считать универсальной формой представления мифологической модели предметов, области и безызбыточной формой модели накопления данных. От канонической структуры переходят к логической структуре информационной базы и к физической организации информационных массивов. Каноническая структура является также основой автоматизации основных процессов предпроектного анализа предметной областей пользователей.
|




 В общем случае под di, dj можно понимать некоторые обобщенные информационные элементы, представляющие собой элементы данных либо группы, составленные из этих элементов: qij=l, если существует взаимосвязь (в том числе возможна и семантическая) между элементами di, dj qij=0 при отсутствии взаимосвязи. Если строка матрицы Q содержит все нулевые элементы, то этой строкой отображаются входные данные. В информационном графе эти данные соответствуют корневым вершинам. Если столбец матрицы Q содержит все нулевые элементы, то он отображает терминальные, т. е. выходные, данные. На информационном графе эти данные соответствуют концевым вершинам. Остальные информационные элементы, отображаемые строками и столбцами матрицы Q, отнесем к групповым элементам. На информационном графе они располагаются в промежуточных вершинах. Объединение множеств значений реквизитов можно выполнить на основе оценки взаимосвязи групповых элементов с подчиненными им выходными. Тогда для группы конечных вершин (терминальных элементов) выделяется множество групповых висячих вершин dr, drÎD. Для множества dr может быть построена матрица достижимости вида Qr, представляющая собой квадратную матрицу с числом строк и столбцов, соответствующим количеству элементов в выделенном множестве dr. При переходе к логическому уровню представления информационной базы информационные элементы и взаимосвязи между ними упорядочиваются по уровням иерархии. Для этого определим множество предшествования и множество достижимости. Для информационного элемента dj матрицы Q множество предшествования П(dj) определяется из совокупности информационных элементов di соответствующих единичной записи в j -м столбце. Анализируя множество H(dj), устанавливают базовые типы структурных элементов, на основе которых формируются информационные группы. Элементам, для которых П(dj)=Æ, соответствуют промежуточные вершины графа. Из матрицы Q для элемента dj выявляют и множество достижимости этих данных D(dj). Это множество формируется за счет элементов di, которым соответствуют единичные записи в j -й строке матрицы Q. Тогда элементы данных dj принадлежат группе r, т. е. определяются как dj, если
В общем случае под di, dj можно понимать некоторые обобщенные информационные элементы, представляющие собой элементы данных либо группы, составленные из этих элементов: qij=l, если существует взаимосвязь (в том числе возможна и семантическая) между элементами di, dj qij=0 при отсутствии взаимосвязи. Если строка матрицы Q содержит все нулевые элементы, то этой строкой отображаются входные данные. В информационном графе эти данные соответствуют корневым вершинам. Если столбец матрицы Q содержит все нулевые элементы, то он отображает терминальные, т. е. выходные, данные. На информационном графе эти данные соответствуют концевым вершинам. Остальные информационные элементы, отображаемые строками и столбцами матрицы Q, отнесем к групповым элементам. На информационном графе они располагаются в промежуточных вершинах. Объединение множеств значений реквизитов можно выполнить на основе оценки взаимосвязи групповых элементов с подчиненными им выходными. Тогда для группы конечных вершин (терминальных элементов) выделяется множество групповых висячих вершин dr, drÎD. Для множества dr может быть построена матрица достижимости вида Qr, представляющая собой квадратную матрицу с числом строк и столбцов, соответствующим количеству элементов в выделенном множестве dr. При переходе к логическому уровню представления информационной базы информационные элементы и взаимосвязи между ними упорядочиваются по уровням иерархии. Для этого определим множество предшествования и множество достижимости. Для информационного элемента dj матрицы Q множество предшествования П(dj) определяется из совокупности информационных элементов di соответствующих единичной записи в j -м столбце. Анализируя множество H(dj), устанавливают базовые типы структурных элементов, на основе которых формируются информационные группы. Элементам, для которых П(dj)=Æ, соответствуют промежуточные вершины графа. Из матрицы Q для элемента dj выявляют и множество достижимости этих данных D(dj). Это множество формируется за счет элементов di, которым соответствуют единичные записи в j -й строке матрицы Q. Тогда элементы данных dj принадлежат группе r, т. е. определяются как dj, если  . На основе этого условия группы итеративно разбиваются по уровням иерархии, начиная с верхнего уровня. Группы самого верхнего уровня называются корневыми группами, поскольку они располагаются в корневых вершинах графа. Группы следующих рангов располагаются в промежуточных вершиных, доступ к которым возможен через корневые группы. Поэтому с помощью корневых групп определяются точки входа к данным информационной базы. Состав информационных элементов, входящих в группу
. На основе этого условия группы итеративно разбиваются по уровням иерархии, начиная с верхнего уровня. Группы самого верхнего уровня называются корневыми группами, поскольку они располагаются в корневых вершинах графа. Группы следующих рангов располагаются в промежуточных вершиных, доступ к которым возможен через корневые группы. Поэтому с помощью корневых групп определяются точки входа к данным информационной базы. Состав информационных элементов, входящих в группу  , можно определить, включив в нее элементы di которым соответствуют единичные записи в j -м столбце матрицы Q. Упорядочивая таким способом элементы матрицы Q, получают структурированный граф, в котором возможные точки входа соответствуют групповым элементам первого уровня, конечные вершины — выходным данным. В промежуточных вершинах располагаются групповые элементы различных уровней иерархии.
, можно определить, включив в нее элементы di которым соответствуют единичные записи в j -м столбце матрицы Q. Упорядочивая таким способом элементы матрицы Q, получают структурированный граф, в котором возможные точки входа соответствуют групповым элементам первого уровня, конечные вершины — выходным данным. В промежуточных вершинах располагаются групповые элементы различных уровней иерархии. могут быть названы элементы
могут быть названы элементы 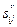 , соответствующие групповым информационным элементам базы. В зависимости от характера групп выделяют
, соответствующие групповым информационным элементам базы. В зависимости от характера групп выделяют  ,
,  . Этим элементам будут соответствовать простые группы. Если
. Этим элементам будут соответствовать простые группы. Если  ,
,  , то получим группы — массивы. Для простых групп образуют простой ключ, для групп массивов — составной ключ, включающий в себя основной и вспомогательный ключи. При этом основной ключ определяется терминальным, конечным элементом, входящим в состав группы массива. Выделение основных ключей должно быть неизбыточным, поэтому необходимо установить и устранить дублируемые терминальные конечные элементы данных.
, то получим группы — массивы. Для простых групп образуют простой ключ, для групп массивов — составной ключ, включающий в себя основной и вспомогательный ключи. При этом основной ключ определяется терминальным, конечным элементом, входящим в состав группы массива. Выделение основных ключей должно быть неизбыточным, поэтому необходимо установить и устранить дублируемые терминальные конечные элементы данных. , соответствует множество терминальных элементов
, соответствует множество терминальных элементов  , а групповому элементу d) — множество терминальных элементов D (d'X Известно, что групповые элементы семантически связаны, если
, а групповому элементу d) — множество терминальных элементов D (d'X Известно, что групповые элементы семантически связаны, если 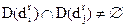 . Соответственно семантическая независимость групповых элементов удовлетворяет условию
. Соответственно семантическая независимость групповых элементов удовлетворяет условию  — уровню иерархии m, причем m<n. При наличии пути на графе из элемента
— уровню иерархии m, причем m<n. При наличии пути на графе из элемента  показывает число путей, ведущих из группы
показывает число путей, ведущих из группы  , то связь является избыточной. Для удаления этой связи заменяем qij= 1 на нулевой элемент. Граф, получаемый после удаления избыточных терминальных элементов и избыточных связей между групповыми элементами данных, определяет каноническую структуру информационной базы. Таким образом, каноническая структура задает логически не избыточную информационную базу. Выделение групповых элементов данных в канонической структуре позволяет объединить множество значений конечных элементов (реквизитов) в логические записи и тем самым упорядочить их в памяти ЭВМ. Структура логических записей и связей между ними должна быть такова, чтобы обеспечить минимум суммарного времени работы с наборами данных как при решении функциональных задач, так и при их корректировке. Поэтому необходимо установить характеристики канонической структуры информационной базы.
, то связь является избыточной. Для удаления этой связи заменяем qij= 1 на нулевой элемент. Граф, получаемый после удаления избыточных терминальных элементов и избыточных связей между групповыми элементами данных, определяет каноническую структуру информационной базы. Таким образом, каноническая структура задает логически не избыточную информационную базу. Выделение групповых элементов данных в канонической структуре позволяет объединить множество значений конечных элементов (реквизитов) в логические записи и тем самым упорядочить их в памяти ЭВМ. Структура логических записей и связей между ними должна быть такова, чтобы обеспечить минимум суммарного времени работы с наборами данных как при решении функциональных задач, так и при их корректировке. Поэтому необходимо установить характеристики канонической структуры информационной базы. где
где  — длина терминального элемента данных. Интегральная оценка длин логических записей может быть произведена на основе вектора
— длина терминального элемента данных. Интегральная оценка длин логических записей может быть произведена на основе вектора 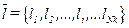 .
. где
где  — время поиска реквизита di при решении задачи на основе алгоритма аj. Значение этого времени зависит от вида обработки реквизита di в выбранном алгоритме (возможна последовательная обработка значений данных либо обработка по ключу). При использовании алгоритмов коррекции корректируются все отношения, которые содержат изменяемый ключевой реквизит и зависимые от него реквизиты. Значение времени работы алгоритма с данными
— время поиска реквизита di при решении задачи на основе алгоритма аj. Значение этого времени зависит от вида обработки реквизита di в выбранном алгоритме (возможна последовательная обработка значений данных либо обработка по ключу). При использовании алгоритмов коррекции корректируются все отношения, которые содержат изменяемый ключевой реквизит и зависимые от него реквизиты. Значение времени работы алгоритма с данными  определяется количеством копий, присутствующих в корректируемых реквизитах. На уровне канонической структуры число копий задается количеством экземпляров терминальных элементов, входящих в группу
определяется количеством копий, присутствующих в корректируемых реквизитах. На уровне канонической структуры число копий задается количеством экземпляров терминальных элементов, входящих в группу  , где
, где  , если
, если  ;
;  , в противном случае. Методика построения канонической структуры информационной базы практически не меняется в зависимости от того, строится централизованная либо распределенная информационная база. При создании распределенной информационной базы матрица Q раскрывается для каждого пользователя. На графе для каждого пользователя формируются групповые и терминальные элементы данных. Полное множество групповых элементов находится путем пересечения групповых элементов данных отдельных пользователей. Таким образом, каноническую структуру информационной базы можно считать универсальной формой представления мифологической модели предметов, области и безызбыточной формой модели накопления данных. От канонической структуры переходят к логической структуре информационной базы и к физической организации информационных массивов. Каноническая структура является также основой автоматизации основных процессов предпроектного анализа предметной областей пользователей.
, в противном случае. Методика построения канонической структуры информационной базы практически не меняется в зависимости от того, строится централизованная либо распределенная информационная база. При создании распределенной информационной базы матрица Q раскрывается для каждого пользователя. На графе для каждого пользователя формируются групповые и терминальные элементы данных. Полное множество групповых элементов находится путем пересечения групповых элементов данных отдельных пользователей. Таким образом, каноническую структуру информационной базы можно считать универсальной формой представления мифологической модели предметов, области и безызбыточной формой модели накопления данных. От канонической структуры переходят к логической структуре информационной базы и к физической организации информационных массивов. Каноническая структура является также основой автоматизации основных процессов предпроектного анализа предметной областей пользователей.


