
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Информационный предел избыточности для канала с пакетными ошибкамиСодержание книги
Поиск на нашем сайте
В коммутируемых каналах появляются пакетные ошибки. Под пакетной ошибкой кратности /понимают ошибку в коде, поражающую i символов. Пакеты ошибок обычно представляются последовательностью плохих состояний канала связи. Выделение хорошего и плохого состояния канала приводит к модели двоичного симметричного канала с памятью. В частном случае группирование ошибок в таком канале может быть описано с помощью простой цепи Маркова. Канал имеет произвольное число состояний, однако должны быть заданы вероятности Pij перехода канала из состояния i в состояние j. Наиболее простой вариант дискретного канала с памятью возникает при наличии двух состояний S0 и S1. Вероятности переходов из одного состояния в другое задаются матрицей
где Р00, Р11 — вероятности сохранения состояний; P00+P01=P10+P11=1 Группирование ошибок возможно при соблюдении условий P01«P00; P10«P11. Данная модель была предложена Э. Гилбертом и предполагает наличие хорошего (безошибочного) состояния с вероятностью сохранения Р00, когда ошибки отсутствуют, и плохого состояния с вероятностью сохранения Р11, когда возникают независимые ошибки с вероятностью искажения символа Р. Вероятности переходов могут быть отображены на графе модели дискретного симметричного канала с памятью, представленного на рис. 50.
Вероятность нахождения канала в хорошем состоянии составляет Сравним вероятность ошибки в двоичном симметричном канале без памяти с вероятностью ошибки в соответствующем канале с памятью. Ошибки возникают в состоянии канала Sl поэтому вероятность ошибки для канала с памятью Тогда матрица переходных вероятностей принимает вид
Видно, что первый столбец матрицы соответствует состоянию канала S0, второй столбец — состоянию S10 и третий столбец — состоянию S11. Модель независимых ошибок для плохого состояния канала связи позволяет аналитическим путем на основе аппарата производящих функций найти вероятность возникновения ошибок на длине кода n. Параметры дискретного симметричного канала с памятью могут быть найдены также на основе обработки результатов экспериментальных исследований канала связи. Обычно вводят функцию распределения длин интервалов между ошибками и связывают параметры модели дискретного канала с памятью с результатами экспериментального исследования канала связи. Исследование коммутируемых телефонных каналов, используемых для передачи данных, показало, что P10»P01, вероятность ошибки может при этом меняться в достаточно широких пределах. Для канала с пакетными ошибками может быть установлен и информационный предел избыточности. Если для передачи информации используется код, исправляющий s ошибок, при кодовом расстоянии d=2s+1, то количество контрольной информации составляет
где M(j,n) — число разновидностей ошибок с длиной пакета j в n элементном коде; Р(j) — вероятность возникновения пакетной ошибки с длиной j
Отсюда
Если допустить, что вероятности возникновения пакетной ошибки любой кратности одинаковы, т. е. Р(0)=Р(1) =... = Р(j) =... = Р1, то получаем
Из условия нормировки вероятностей
Количество контрольной информации
Информационный предел избыточности kmin=IK для двоичного кода. Отсюда число контрольных элементов составляет
В соответствии с этим информационным пределом могут быть построены корректирующие коды, которые оказываются целесообразными при равновероятных пакетных ошибках в дискретных каналах связи. Модель Э. Гилберта является простейшей моделью дискретного симметричного канала с памятью. Некоторым обобщением этой модели может быть допущение ошибок не только в плохом, но и в хорошем состоянии. При этом матрица переходных вероятностей P(S) сохраняет свою справедливость, вводятся вероятности ошибки в хорошем Р(0) и плохом Р(1) состояниях. Связь с введенной ранее вероятностью ошибки Р определяется выражением Р=Р(0)Р0+Р(1)Р1. Развитием модели Э. Гилберта может быть введение ряда состояний каналов связи с соответствующими реальными значениями вероятностей ошибки. Большое значение на практике приобретают модели каналов связи, полученные на основе экспериментального исследования. Существует большое число таких моделей, которые пригодны для конкретных, достаточно ограниченных случаев применения.
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 291; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.160.29 (0.008 с.) |

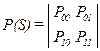 ,
,
 , соответственно вероятность нахождения канала в плохом состоянии —
, соответственно вероятность нахождения канала в плохом состоянии —  .
. . Нетрудно видеть, что Р п«Р. Выделение плохого состояния канала связи позволяет моделировать пакеты ошибок как последовательность плохих состояний. Длина этих последовательностей обычно описывается геометрическим распределением. Пакеты ошибок накладываются на кодовую комбинацию, но не всегда вызывают искажение символа. Поэтому плохое состояние канала S1 может быть подразделено на два состояния: правильное выявление элементов кода и ошибка в выявлении. Плохое состояние канала с правильным выявлением элементов обозначим S10, плохое состояние с ошибочным выявлением — S11 (рис. 51).
. Нетрудно видеть, что Р п«Р. Выделение плохого состояния канала связи позволяет моделировать пакеты ошибок как последовательность плохих состояний. Длина этих последовательностей обычно описывается геометрическим распределением. Пакеты ошибок накладываются на кодовую комбинацию, но не всегда вызывают искажение символа. Поэтому плохое состояние канала S1 может быть подразделено на два состояния: правильное выявление элементов кода и ошибка в выявлении. Плохое состояние канала с правильным выявлением элементов обозначим S10, плохое состояние с ошибочным выявлением — S11 (рис. 51).
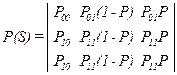 .
.
 ,
, .
.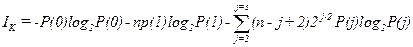 .
. .
. P(j)=1. Отсюда
P(j)=1. Отсюда .
. .
. .
.


