
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Информационный граф системы обработкиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
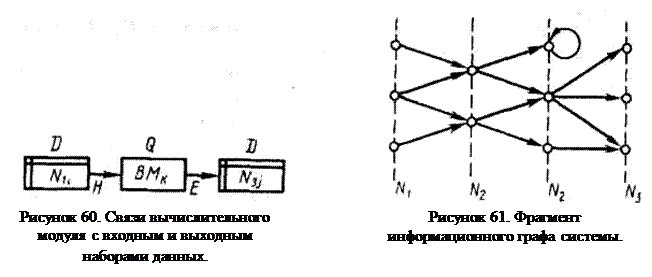
Набор данных есть совокупность данных, передаваемых между двумя вычислительными модулями. На логическом уровне выделяют связи по управлению и связи по данным. Такие связи существуют как внутри вычислительного модуля, так и между модулями различных уровней вычислительного графа системы обработки. Для любого модуля выделяют входные и выходные данные. Входные данные отобразим матрицей Н, элемент которой hik=1, если входной набор данных N1i используется вычислительным модулем k. Этот же элемент hik=0, если это не имеет места. Выходные данные формально отобразим матрицей Е, элемент которой ekj=1, если набор данных N3j получен в результате работы вычислительного модуля k. Элемент матрицы ekj=0 — в противном случае. Матрица взаимосвязи входных и выходных данных Q=HÄE. Элемент матрицы qij=1, если входной набор данных N1i используется для получения выходного набора данных N3j. Элемент матрицы qij=0, если это не имеет места. На рис. 3.26 представлена связь вычислительного модуля ВМk с входным набором данных N1i и выходным набором данных N3j.
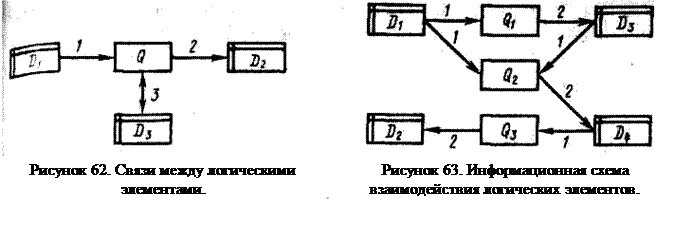
Структура модуля по преобразованию данных задается матрицей Q, связь модуля с набором данных N1i определяется матрицей Н, связь модуля с набором данных N3j — матрицей Е. Матрица Q соответствует ориентированному графу взаимосвязей между данными (этот граф получил название информационного графа системы). Вершинами графа являются родные, промежуточные и выходные наборы данных. Дуги графа отображают информационные связи между этими наборами (рис. 61). В информационном графе системы можно выделить входные вершины, которые не имеют входных дуг и отображают первичные (входные) наборы данных. В концевых вершинах графа, которые не имеют исходящих дуг, располагаются выходные наборы данных, являющиеся результатами обработки информации и используемые для принятия решения в системе. В остальных вершинах графа располагаются промежуточные наборы данных, которые являются внутренними по отношению к пользователю и возникают в процессе вычислений как промежуточный результат. Отметим, что в отличие от вычислительного графа системы информационный граф может иметь контуры и петли, что объясняется необходимостью повторного обращения к отдельным наборам данных. Входные данные являются первичными, поскольку они возникают при изучении производства и характеризуют исходное состояние управляемой системы. Промежуточные и выходные данные относятся ко вторичным данным. Вторичные данные возникают в результате процесса обработки, т. е. выполнения отдельных процедур над первичными данными. Вычислительный граф системы обработки и информационный граф системы позволяют формализованно определить инфологическую модель предметной области. В процессе обработки и накопления данных формируются новые наборы данных, при этом можно различать два крайних случая: 1. Формирование набора данных на основе вычислительного алгоритма, т. е. для имеющихся входных наборов данных на основе вычислений получают выходные данные. Последовательность использования вычислительных модулей для формирования выходного набора данных определяется вычислительной граф-схемой алгоритма в виде ориентированного графа без петель. В вершинах графа располагаются вычислительные модули, а дуги графа отображают отношение предшествования между ними. 2. Вычисление значений набора данных по имеющимся старым значениям и по совокупности изменений, возникающих в первичном наборе данных. Эти процедуры осуществляются на основе алгоритмов корректировки набора данных. Корректировка возможна в том случае, если корректируемый набор данных уже ранее был запрошен и хранится в информационной базе. Таким образом, в модели накопления данных может быть выявлено два основных типа алгоритма нахождения новых наборов: вычислительный алгоритм и алгоритм корректировки набора данных. Реализация вычислительного алгоритма при запросе обычно необходима тогда, когда запрашиваемый набор данных не хранится в информационной базе. При наличии этого набора более удобно использовать алгоритм корректировки. Вычислительный алгоритм реализуется на базе информационного графа системы, алгоритм корректировки базируется на списке изменений, вносимых в первичный набор данных. Независимо от используемого алгоритма вычислительный модуль выполняет определенные процедуры, включающие в себя действия над данными. На логическом уровне возникает задача спецификации действий, т. е. определение входных и выходных наборов данных для действий, а также взаимосвязей между различными действиями. При этом можно выделить два типа функциональных (логических) элементов: элементы — действия Q и элементы — объекты действий D. Элементы действия Q характеризуются внешними связями и ресурсами. Такой элемент реализует определенное преобразование над данными с использованием в качестве ресурсов элементов типа Q и элементов типа D. В качестве объектов действий выступают данные, которые характеризуются именем, типом и значением. Тип определяет множество значений, которые принимают объекты данного типа. Объект действий задается структурой, т. е. составом компонентов и связей между ними. Элемент Q взаимодействует с элементами D1, D2, D3 через связи типа: 1 — «вход», 2 — «выход», 3 — «вход — выход» (рис. 62).
Совокупность элементов действий Q и элементов объектов действий, т. е. данных D, образует информационную схему. Естественно, что одни и те же данные могут быть использованы различными элементами действий. На рис. 63 представлена информационная схема, включающая элементы действий Q1…Q3 и элементы данных D1…D4. В схеме присутствуют связи типа 1 — «вход» и типа 2 — «выход». Связи первого типа формально записываются в виде D in Q, а второго типа — D out Q. Информационная схема отображается матрицей
Матрица В построена непосредственно по информационной схеме. Данные D1 используются действиями Q1 и Q2, что соответствует первой строке матрицы. Данные D2 формируются действием Q3 что отображается второй строкой матрицы. Данные D3 вычисляются действием Q1 и используются действием Q2, что соответствует третьей строке. Данные D4 вырабатываются действием Q2 и используются действием Q3 (четвертая строка). Исключим из информационной схемы элементы действия Q и найдем связи по данным, что на логическом уровне соответствует информационному графу системы. Учтем при этом частоту активизации действий. При одиночном запросе суммарное количество действий, использующих данные di, обозначим через zii, а суммарное количество действий, использующих данные dj совместно с данными di, определим как zij. Члены zij, zij являются элементами матрицы Z=B´Bt. Для рассмотренного примера
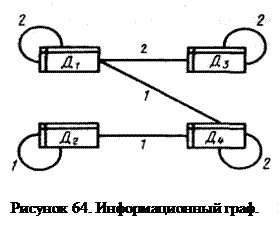
Полученной матрице будет соответствовать граф, изображенный на рис. 64.
В вершинах этого графа располагаются элементы данных D1...D4, Дуги графа отображают суммарное количество действий, использующих эти данные раздельно и совместно. Вводя в матрицу Z частоту активизаций действий f, получим матрицу ZF=(B·f)´Bt. Элемент матрицы zfij показывает частоту использования данного di с учетом частоты активизации действий. Соответственно элемент zfij отображает частоту совместного использования данных di, dj. По значениям этих частот данные могут объединяться в записи, а записи — в массивы. При этом обеспечивается минимизация числа обращений к записям в процессе обработки и корректировки информации. При известной частоте активизации действий, заданной матрицей — строкой f, нетрудно по приведенной выше методике найти ZF. Например, для f=|1 2 5|
На основе полученной матрицы данные могут быть скомпонованы в записи с учетом частоты их совместного использования. Учитывая, что в основе современной информационной технологии лежат данные, возникает задача выделения и локализации сильно связанных элементов данных. Если в информационном графе системы содержится N вершин и граф отображает полносвязанную систему, то максимальное число связей составит N2. Для определения степени связности графа, представленного на рис. 64, найдем коэффициент совместного использования данных di, dj в виде
Элементы главной диагонали этой матрицы характеризуют внутреннюю связность элементов данных, остальные элементы матрицы определяют связность их между собой. При sij=0 для i¹j Получаем разделение данных на независимые компоненты. Коэффициент связности При отсутствии внешних связей ks оut=0, кs=кs in. Внутренняя связность данных может быть определена в виде
|
||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 805; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |


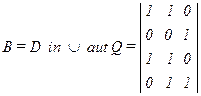 .
.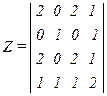 .
.
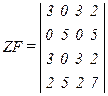 .
.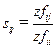 . Элемент sij=1, если данное di всегда используется совместно с данным dj. При sij=0 данные di, dj совместно не используются. Объединяя sij при l≤i≤N, j≤l ≤N, находим матрицу коэффициентов совместного использования данных. Для рассмотренного графа N=4 получаем
. Элемент sij=1, если данное di всегда используется совместно с данным dj. При sij=0 данные di, dj совместно не используются. Объединяя sij при l≤i≤N, j≤l ≤N, находим матрицу коэффициентов совместного использования данных. Для рассмотренного графа N=4 получаем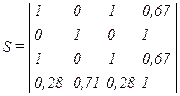 .
.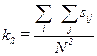 , он определяется совокупностью вутренних и внешних связей элементов данных, т. е. ks=ks in+ks оut.
, он определяется совокупностью вутренних и внешних связей элементов данных, т. е. ks=ks in+ks оut.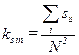 . В качестве критерия реорганизации информационной схемы используют зачастую относительный коэффициент связности
. В качестве критерия реорганизации информационной схемы используют зачастую относительный коэффициент связности 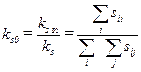 . Объединение отдельных сильно связанных элементов данных позволяет увеличить значение относительного коэффициента связности. Этот коэффициент может быть изменен, если перераспределяются функции между элементами действий.
. Объединение отдельных сильно связанных элементов данных позволяет увеличить значение относительного коэффициента связности. Этот коэффициент может быть изменен, если перераспределяются функции между элементами действий.


