
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Потери при информационном взаимодействииСодержание книги
Поиск на нашем сайте
Оценим потери информации, возникающие по причине внешних и внутренних мешающих воздействий, используя результаты теории информация-Процесс информационного взаимодействия источника (И) и потребителя (П) может осуществляться с помощью системы (С) путем последовательного обмена сообщениями (рис. 38).
Тогда система реализует процесс отражения, т. е. информация от источника в виде последовательности сообщений с помощью системы выдается потребителю. Рассмотрим случай, когда множества сообщений Хо, Yо конечны. Будем считать, что в процессе отражения сообщение y0i возникшее на входе системы, порождает на выходе y0i. Сообщение у0i возникает как результат сообщения x0j в итоге реализации информационного процесса в системе. Качественное функционирование системы предполагает минимизацию потерь информации при таком преобразовании. Поэтому полезно сравнить количество информации, которое содержится в сообщении x0j, и количество информации в сообщении у0i относительно сообщения x0j. Количество собственной информации сообщения x0j составит I(x0j) =-log2P(x0j), где P(x0j) — вероятность возникновения на выходе источника сообщения x0j. Значение собственной информации в сообщении x0j потребителю неизвестно. Он судит о нем лишь по сообщению yOi. Тогда количество собственной информации в сообщении у0i составит I(y0i)=-log2P(y0i), где Р(у0i)) - вероятность возникновения сообщения у0i на входе потребителя. Как было выше показано, для нахождения полезной информации необходимо устранить информацию, вносимую помехами. Она выражается в виде условной собственной информации
Усредняя полученное выражение по множествам сообщений Хо, Yo, найдем количество взаимной информации, т. е. среднее количество информации, которое связывает ансамбли I(X0,Y0)=M{I(x0j, у0i)}. Учитывая, что сообщение x0j возникает с вероятностью P(x0j), а сообщение y0i с вероятностью P(x0j)P(y0i/x0j), окончательно получим
где H(Y0) — безусловная энтропия по множеству сообщений Y0, Если сообщение y0i тождественно сообщению x0j, то вероятность Р(y0i)=Р(х0j), т.е. P(y0i/x0j). Тогда условная энтропия В реальных условиях имеют место внутренние и внешние возмущения, которые вызывают потери информации, отображаемые членом В канале возмущений осуществляется преобразование множества сообщений Х0 во множество сообщений У0, и взаимная информация I(Х0, У0) может рассматриваться как количество информации, проходящей через канал возмущений. К этому каналу тогда могут быть отнесены потери информации при реализации информационного процесса, выражаемые членом
Избыточность может быть направлена на обнаружение и исправление ошибок. Численно вносимая избыточная информация должна соответствовать информации потерь
где Р0 — вероятность ошибки, одинаковая для каждого сообщения. Если вероятность ошибки зависит от номера принимаемого сообщения, то определяют среднюю вероятность ошибки
где
Количество избыточной информации, необходимое для исправления ошибки, найдем из условия равновероятности переходов сообщения в любое другое. Каждое сообщение из множества Хо может при переходе через обобщенный канал связи с одинаковой вероятностью трансформироваться в любое из (М-1) сообщений. Воспользуемся формулой энтропии для равновероятных событий, тогда неопределенность попадания любого сообщения в одну из точек множества М-1 составит Н=log2(М-1). Так как такое попадание имеет место с вероятностью ошибки Ро, то Ни=Р0log2(М-1). Окончательно получаем, что количество необходимой избыточной информации для компенсации потерь, возникающих при реализации информационного процесса, составит
Отметим, что полученное выражение задает нижний уровень избыточности для случая независимых ошибок. Он может быть реализован за счет рационального выбора кода при согласовании источника и потребителя информации. Таким образом, потери информации, выражаемые условной энтропией, могут служить обобщенной характеристикой качества реализации информационного процесса. Для компенсации потерь информации в информационные системы вводят избыточность, которая может реализовываться на концептуальном, логическом и физическом уровнях. Концептуальный уровень введения избыточности означает наличие избыточных сообщений за счет существования коррелированных значений информации, снимаемых с реального объекта. Избыточной является и человеческая речь. На логическом уровне избыточность закладывается в код, отображающий сообщение, путем специального конструирования обнаруживающих и исправляющих кодов. Здесь же могут находить применение системы с обратной связью, позволяющие поднять верность преобразования информации. На физическом уровне избыточность закладывается в сигнал, отображающий отдельные составные части кода, т. е. его элементы. По существу избыточность сигнала тем больше, чем сильнее различаются отдельные значения сигналов. Геометрическое представление сигнала в пространстве позволяет найти наилучшие условия расположения сигналов, обеспечивающих максимальное отличие их значений. Если для построения кода используются сигналы х1(t), х2(t), представленные векторами в двумерном пространстве, то характеристикой их различия служит кодовое расстояние d, определяемое по проекциям этих сигналов (рис. 40):
где х 11, x21 — проекции сигналов на ось 1; x12, x22 — проекции сигналов на ось 2.
Если для реализации кода используется n сигналов, то они изображаются в n-мерном пространстве и кодовое расстояние между сигналами х1(t), х2(t) определяется как
где x1j, x2j — проекции первого и второго сигналов на ось j. Если сигналы х1(t), х2(t) непрерывны в интервале длительности Т, то можно найти кодовое расстояние в виде
Полагая, что амплитуды сигналов одинаковые, т. е. x1(t)=x2(t), получим
где Еc — энергия сигнала, пропорциональная квадрату амплитуды, l12 — коэффициент корреляции первого и второго сигналов. Для увеличения кодового расстояния необходимо увеличивать энергию сигнала Ес и получить отрицательный коэффициент корреляции l12. Это означает, что при наличии двух сигналов они должны быть противоположны по фазе. Нетрудно показать, что при использовании л сигналов в целях повышения кодового расстояния они должны располагаться в пространстве таким образом» чтобы концы их векторов упирались в вершины правильного многоугольника, а начала векторов находились в центре его тяжести. При равенстве амплитуд сигналов соотношения между коэффициентом корреляции и энергией сигнала составит Качество реализации любого информационного процесса оценивается вероятностно-временными характеристиками, которые устанавливаются на основе аналитического исследования с использованием математической модели либо на базе машинного эксперимента, проводимого на имитационной модели. Исходной информацией при построении модели являются данные о назначении и условиях реализации информационного процесса. В зависимости от уровня абстрагирования и цели моделирования выбираются соответствующие математические схемы, которые позволяют построить модели идеально функционирующей системы, модель случайных воздействий, модель внешней среды и модель взаимодействия системы с внешней средой. С помощью математической схемы моделирования можно перейти от концептуального (содержательного) описания моделей информационного процесса к логическому (формальному) описанию с учетом воздействий внешней среды и границы «система — среда». Описание информационного процесса на модели осуществляется в виде выбора совокупности входных воздействий, воздействий внешней среды, внутренних параметров процесса и выходных характеристик системы. Входные воздействия, воздействия внешней среды и внутренние параметры системы являются независимыми переменными модели, а выходные характеристики процесса — это зависимые переменные. Определение выходных характеристик осуществляется на базе алгоритма функционирования модели. Один и тот же информационный процесс может быть реализован различными алгоритмами функционирования. Ранее было показано, что взаимодействие между территориально удаленными объектами осуществляется за счет обмена данными. Доставка данных производится по заданному адресу с использованием сетей передачи данных. В условиях распределенной обработки информации эти сети превращаются в информационно-вычислительные, однако для них остаются характерными проблемы передачи, распределения и доставки данных по заданным адресам. Важнейшим звеном сети является канал передачи данных, структурная схема которого Представлена на рис. 41. Физической средой передачи данных является некоторый реальный либо специально организуемый канал связи (КС), в котором элементы данных передаются в виде физических сигналов. Такой канал получил название непрерывного канала, поскольку сигналы описываются непрерывными функциями времени.
Согласование сигнала и канала связи осуществляется по физическим характеристикам, а также по соотношению скорости передачи информации и пропускной способности непрерывного канала. Следует отметить, что большинство непрерывных каналов оказываются непригодными для передачи сигналов, отображающих данные, без предварительного их преобразования. Поэтому сигналы по физическим характеристикам должны быть согласованы со свойствами непрерывного канала связи, для чего в структуре канала передачи данных предусматривают устройства преобразования сигналов, которые для телефонных каналов связи приобретают характер модемов. Модем представляет собой совокупность модулятора (М) и демодулятора (ДМ). С помощью модулятора сигнал воздействует на некоторый параметр переносчика, благодаря чему спектр сигнала смещается в область частот, для которых наблюдается наименьшее затухание в выбранном непрерывном канале связи. Обратную операцию, т. е. переход от модулированного сигнала к модулирующему, осуществляет демодулятор. Модулятор, непрерывный канал связи и демодулятор образуют дискретный канал, на входе и выходе которого существует множество дискретных элементов кода. На логическом уровне может быть построена модель дискретного канала связи, которая отображает процесс передачи через этот канал дискретных элементов кода. Дискретный канал связи должен быть так сконструирован, чтобы скорость передачи согласовывалась с его пропускной способностью. Для обеспечения помехоустойчивой передачи информации в структуру канала передачи данных вводят устройство защиты от ошибок (УЗО). Оно обеспечивает помехоустойчивое кодирование-декодирование, соответствующий режим функционирования системы передачи данных (с обратной связью, с адаптацией и т. д.), а также режим формирования совокупности данных в виде кадра. Источники (ИС) и потребители сообщений (ПС) согласуются с каналом передачи данных с помощью устройств сопряжения УС. Таким образом, как на передающей, так и на приемной стороне используется оконечное оборудование данных (ООД). Стык между оконечным оборудованием и аппаратурой передачи, реализующей дискретный канал, унифицируется в рамках международных и национальных рекомендаций. Стык обычно задается на физическом уровне. Канал передачи данных является основной составной частью сети обмена данными, в которой процесс передачи реализуется на основе принятого метода коммутации и принципа маршрутизации данных. Рассмотрим канал передачи данных на логическом уровне. В основе его лежит модель дискретного канала связи.
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 351; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.161.119 (0.013 с.) |


 . Тогда количество информации в сообщении у0i относительно сообщения x0j составит
. Тогда количество информации в сообщении у0i относительно сообщения x0j составит
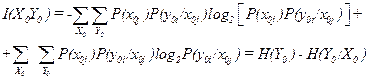 ,
, — условная энтропия по множеству сообщений Y0 при уловии, что множество событий Х0 известно.
— условная энтропия по множеству сообщений Y0 при уловии, что множество событий Х0 известно. и взаимная информация есть энтропия H(Y0). Это означает, что имеем идеальную систему, которая высококачественно отображает реальность, и информационный процесс реализуется в системе без потерь.
и взаимная информация есть энтропия H(Y0). Это означает, что имеем идеальную систему, которая высококачественно отображает реальность, и информационный процесс реализуется в системе без потерь.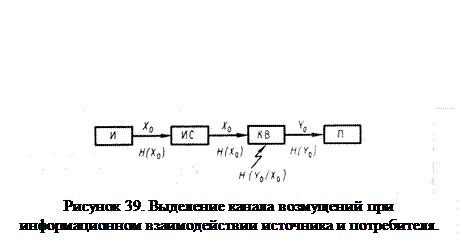
 , где Но, Ни — количество информации, необходимое для обнаружения и исправления ошибок соответственно. Физически Н0 — энтропия двух событий, одно из которых отображает наличие ошибки с вероятностью Р0, а второе — отсутствие ошибок с вероятностью 1-Р0. Тогда
, где Но, Ни — количество информации, необходимое для обнаружения и исправления ошибок соответственно. Физически Н0 — энтропия двух событий, одно из которых отображает наличие ошибки с вероятностью Р0, а второе — отсутствие ошибок с вероятностью 1-Р0. Тогда ,
,
 — вероятность ошибки в i -м сообщении:
— вероятность ошибки в i -м сообщении: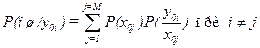 .
.
 ,
,
 .
. .
. ,
, , где n — число сигналов. Наилучшие условия различения наблюдаются при использовании двух сигналов. Тогда l=-Ес и кодовое расстояние определяется энергией сигнала. Таким образом, на физическом уровне реализация информационного процесса должна проходить при таких энергиях сигналов, которые намного превышают энергию помехи. В этом случае повышается их различимость.
, где n — число сигналов. Наилучшие условия различения наблюдаются при использовании двух сигналов. Тогда l=-Ес и кодовое расстояние определяется энергией сигнала. Таким образом, на физическом уровне реализация информационного процесса должна проходить при таких энергиях сигналов, которые намного превышают энергию помехи. В этом случае повышается их различимость.



