
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Достаточные условия эргодичностиСодержание книги
Поиск на нашем сайте
Теорема 1. Стационарный случайный процессССП X(t) эргодичен относительно математического ожидания, еесли его корреляционная функция
и при этом:
Теорема 2. Стационарный случайный процессССП X(t) эргодичен относительно дисперсии, если корреляционная функция стационарного слу- чайного процесса ССП Y(t)=X2(t) стремится к нулю0 при τ→∞; при этом:
Теорема 3. Стационарный случайный процесс ССП X(t) эргодичен относительно корреляционной функции, если стремится к нулю при τ→∞ кор- реляционная функция стационарного случайного процессаССП Z(t, τ)= пПри этом:
При практических расчетах интервал (0;Т) разбивается на n равных частей Если ограничиться формулой прямоугольников, получаем
m=0, 1, 2, …, n-1. Пример 14. X(t) – эргодический стационарный случайный процессССП,: V – случайная величинаСВ, имеющая математическое ожидание mvmv и дисперсию Dv (Dv≠0);. X(t)и V независимы. Исследовать на эргодичность случайный процессСП Y(t): Y(t)=X(t)+V, если X(t)и V независимы..
Решение. Так как случайный процессСП X(t) и случайная величинаСВ V независимы, то mY(t)=mX(t)+mv; k KY(τ)=kKX(τ)+Dv. При этом
Следовательно, случайный процессСП Y(t) не является эргодичным по математическому ожиданию; то есть наложение на эргодический случайный процессСП независимой случайной величиныСВ разрушает эргодичность.
Пример 15. Рассматривается простейший поток событий с интенсивностью λ. Случайный процесс X(t) принимает значения +а и –а (а>0);, при этом X(t) скачком меняет свое состояние с +а на –а или наоборот в момент наступления очередного события в потоке. Найти характеристики случайного процессаСП X(t).
Решение.
происходят в произвольные моментты времени (см. рис.), поэтому для любого значения t с равной вероятностью ½ СП X(t) может принимать значения и +а, и –а; Поэтому одномерный закон распределе- ния каждого сечения очевиден (см. таб- лицу). Получаем
mMxХ(t)=-a·0,5+a·0,5=0; DxХ(t)=(-a)2·0,5+a2·0,5=a2.
Корреляционная функция имеет вид:
=M(X(t1)X(t2)). Произведение X(t1)X(t2) может принимать только два значения: 1) –а2, если в интервале (t1, t2) в простейшем потоке произошло нечетное число событий; 2) а2, если в интервале (t1, t2) в потоке происходит четное число событий. Вероятность k К событий на временном промежутке τ=t2-t1 (τ≥0) в простейшем потоке с интенсивностью λ находится по формуле Пуассона:
Поэтому полная вероятность всех четных kK имеет вид:
Получаем следующее значение корреляционной функции:
Окончательно,
то есть случайный процессСП X(t ) стационарен и эргодичен.
Пример 16. По заданной реализации эргодического случайного процесса X(t) найти приближенные значения его характеристик.
Решение. Временной интервал (0;20) разобьем на 10 интервалов точками 0, 2, 4,…, 20. В качестве расчетных моментов времени выбираем середины полученных интервалов:
Математическое ожидание:
Дисперсия:
Корреляционная функция:
m=0: k KX(0)≈DX=6,65 m=1:
m=2:
m=3:
m=4:
m=5:
m=6:
m=7: m=8: m=9:
Глава 6. Спектральная теория стационарных случайных Процессов ССП Понятие спектрального разложения стационарного случайного ПроцессаССП. Дискретные и непрерывные спектры. Спектральная плотность и ее свойства
Элементарный стационарный случайный процессСП Случайный процесс X(t) вида X(t)=Ucosωt+Vsinωt, где U и V – центрированные некоррелированные случайные величиныСВ; DU=DV=σ2, ω – const; называется элементарным стационарным случайным процессомСП. Как следует из Примера 11, mX(t)=0; KX(t1;t2)=kKX(τ)=σ2cosωτ, τ=t2-t1; DX(t)=σ2, следовательно, X(t) – стационарный в широком смысле случайный процессСП. Часто его записывают в виде гармоники
со случайной амплитудой
Сумма конечного числа гармоник
где Up и Vp – центрированные некоррелированные случайные величиныСВ; DUp=-DVp= Легко показать, что mX(t)=mX;
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 722; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.94.64 (0.007 с.) |

 стремится к нулю при τ→∞;
стремится к нулю при τ→∞; .
.
 ;(X(t+τ)-mx) стремится к нулю при τ→∞.
;(X(t+τ)-mx) стремится к нулю при τ→∞.
 в каждом промежутке выбирается точка ti(например, середина).
в каждом промежутке выбирается точка ti(например, середина).

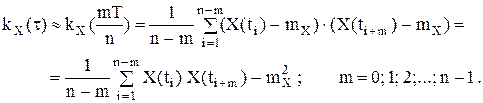


 ППо смыслу задачи события в потоке
ППо смыслу задачи события в потоке KX(t1;t2)=M((X(t1)-mX)×(X(t2)-mX))=
KX(t1;t2)=M((X(t1)-mX)×(X(t2)-mX))=


 (τ≥0).
(τ≥0). kKX(τ)→0 при τ→∞,
kKX(τ)→0 при τ→∞,
 X2(ti)
X2(ti)



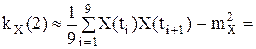
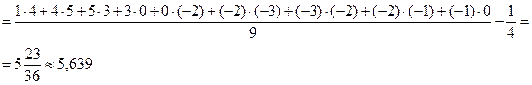
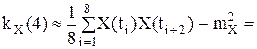



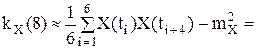

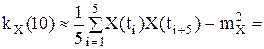

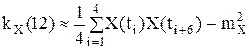 =
=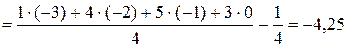







 ,
, 
 , случайной фазой ωt+arctgU/V и частотой ω.
, случайной фазой ωt+arctgU/V и частотой ω.
 .
.




