
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Среднеквадратическоие отклонениея.Содержание книги
Поиск на нашем сайте
Если в каждом сечении случайного процесса существует математическое ожидание, то математическим ожиданием случайного процесса X(t) называется неслучайная функция mxX(t), значение которой при каждом фиксированном значении t равно математическому ожиданию соответствующего сечения: mxX(t)=MX(t). Основные свойства математического ожидания случайного процесса: если φ(t) - неслучайная функция, то М φ(t)=φ(t); М(φ(t)×X(t))=φ(t)×mxX(t); M(X1(t)+X2(t))= Если в каждом сечении случайного процесса существует дисперсия, то дисперсией случайного процесса X(t) называется неслучайная функция DxХ(t), значение которой при каждом фиксированном значении аргумента t равно дисперсии соответствующего сечения: DxX(t)= DХ(t)= M(X(t)-+mxX(t))2.
Основные свойства дисперсии случайного процесса: если φ(t) - неслучайная функция, то D(φ(t))=0; D(φ(t)×X(t))=φ2(t)×DxX(t); D(X(t)+φ(t))=DxX(t );
Среднеквадратическим отклонением случайного процесса X(t) называется арифметический квадратный корень из его дисперсии:
Корреляционная функция случайного процесса и ее свойства. Нормированная корреляционная функция Корреляционной функцией случайного процесса X(t) называется неслучайная функция KxX(t1; t2) двух независимых аргументов, значение которой равно корреляционному моменту сечений, соответствующих моментам времени t1 и t2: KxX(t1; t2)=M((X(t1)-mxX(t1))×(X(t2)-mxX(t2))).
Основные свойства корреляционной функции:
2) KxX(t; t)=DxX(t); 3) KxX(t1; t2)= KxX(t2; t1);
4) если φ(t) - неслучайная функция, то
Kφ(t)(t1; t2)=0; Kφ(t)+-xX(t)(t1; t2)= Kx(X(t)(t1; t2); Kφ(t)×Xx(t)(t1; t2)= φ(t1)× φ(t2)×KxX(t)(t1; t2);
5) 6 ) Функция вида
Называется нормированной корреляционной функцией. Взаимная корреляционная функция и нормированная взаимная Корреляционная функция двух случайных процессов Взаимной корреляционной функцией двух случайных процессов X(t) и Y(t) называют неслучайную функцию RxXYy(t1; t2) двух независимых аргументов t1 и t2, значение которой равно корреляционному моменту сечений этих случайных процессов в соответствующие моментыпромежутки времени: RxXYy(t1; t2)= M((X(t1)-mxX(t1))×*(Y(t2)-mmyY(t2))).
Свойства взаимной корреляционной функции: если φ(t) и Ψ(t) - неслучайные функции, то
RxX(t)+φ(t) yY(t)+Ψ(t)(t1; t2)= RxXYy(t1; t2); RxX(t)×*φ(t) yY(t)×*Ψ(t)(t1; t2)= φ(t1)× Ψ(t2)×RxXYy(t1; t2); RxXYy(t1; t2)=RyYXx(t21; t1 t);
Функция вида
Называется нормированной взаимной корреляционной функцией случайных процессов X(t) и Y(t).
Вероятностные характеристики суммы двух случайных величин Теорема 1. Математическое ожидание суммы двух случайных процессов X(t) и Y(t) равно сумме их математических ожиданий: m mx+X+Yy(t)= mX(t)mx(t)+myY(t).
Теорема 2. Корреляционная функция суммы двух случайных процессов
X(t) и Y(t) имеет вид: KxX+Yy(t1; t2)=KxX(t1; t2)+KyY(t1; t2)+RxXYy(t1; t2)+RyYXx(t2; t1 t1). ).
Следствие 1. Если случайные процессы X(t) и Y(t) нек коррелированны, то KxX+Yy(t1; t2)=KxX(t1; t2)+KyY(t1; t2); DxX+Yy(t)=DxX(t)+DyY(t).
Следствие 2. Если случайный процесс X(t) и случайная величина Y некне коррелированны, то KxX+Yy(t1; t2)=KxX(t1; t2)+DyY.
Пример 3. Рассматривается случайный процесс Y(t)=X×e-t (t≥0), где X - нормально распределенная с параметрами m и σ случайная величина. Найти математическое ожидание, дисперсию, корреляционную и нормированную корреляционные функции, одномерную плотность распределения.
Решение. Математическое ожидание: mY(t)=M(Xe-t)=e-tmX=me-t. Дисперсия: DY(t)=D(Xe-t)=e-2t DX=σ2e-2t. Стандартное отклонение: Корреляционная функция: KY(t1; t2)=M((X = Нормированная корреляционная функция:
По условию задачи случайная величина X распределена нормально; при фиксированном значении t сечение Y(t) линейно зависит от случайной величины X, и по свойству нормального распределения сечение Y(t) также распределено нормально с одномерной плотностью распределения:
Пример 4. Найти основные характеристики случайного процесса Y(t)=W×e-Ut (t>0), где W и U - независимые случайные величины; U распределена равномерно на отрезке [0; а]; W имеет математическое ожидание mW и стандартное отклонение σW.
Решение. Математическое ожидание: mY(t)=M(We-Ut)=MW×M(e-Ut)=mw×*M(e-Ut);
Корреляционная функция:
так как то Дисперсия:
Пример 5. Найти одномерный закон распределения случайного процесса: Y(t)=Vcos(Ψt-U), где V и U независимые случайные величины; V нормально распределена с параметрами (mV; σV); Ψ-const; U- равномерно распределена на отрезке [0; 2π].
Решение. Математическое ожидание случайного процесса Y(t):
Дисперсия:
Стандартное отклонение: Переходим к выводу одномерного закона распределения. Пусть t-фиксированный момент времени, и случайная величина U принимает фиксированное значение U=u - const; u M(Y(t)| U=u)=mV×cos(Ψt-u); D(Y(t)| U=u)= σ(Y(t)| U=u)= Так как случайная величина V распределена нормально и при заданном значении случайной величины U=u все сечения линейно зависимы, то условное распределение в каждом сечении является нормальным и имеет следующую плотность:
Безусловная одномерная плотность случайного процесса Y(t):
Очевидно, что это распределение уже не является нормальным.
|
||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 565; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.186.194 (0.009 с.) |

 mx1(t)+mx2(t); M(X(t)+φ(t))= mxX(t)+ φ(t).
mx1(t)+mx2(t); M(X(t)+φ(t))= mxX(t)+ φ(t). .
. .
.






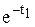 e-t1-m
e-t1-m  e-t1)×(X
e-t1)×(X  e-t2-m
e-t2-m  e-(t1+t2) M(X-m)2=σ2
e-(t1+t2) M(X-m)2=σ2 


 , (t>0).
, (t>0).



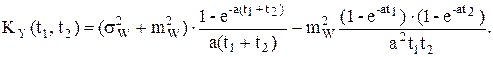


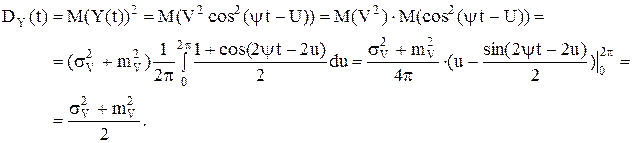

 [0; 2π], тогда получаем следующие условные характеристики случайного процесса Y(t):
[0; 2π], тогда получаем следующие условные характеристики случайного процесса Y(t): ×cos2(Ψt-u);
×cos2(Ψt-u); ×|cos(Ψt-u)|.
×|cos(Ψt-u)|.




