
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейный регрессионный анализ экспериментальных данныхСодержание книги Поиск на нашем сайте
При экспериментальном исследовании взаимосвязи двух и более случайных величин удобно иметь модель этой связи, которая дала бы возможность предсказать значения одной случайной величины по конкретным значениям другой. Характерным примером является рассмотренный в данной лабораторной работе закон Хика, говорящий о наличии в общем случае линейной модели связи между временем реакции оператора и количеством обрабатываемой оператором информации. Логичен следующий шаг: конкретизировать эту связь для каждого испытуемого так, чтобы по величине предъявляемой информации можно было бы предсказать время его сенсомоторной реакции выбора. Методы решения подобных задач носят название "регрессионный анализ". Итак, согласно закону Хика имеется линейная связь между временем реакции Т и количеством предъявляемой оператору информации I: T = AI + B, (3.15) Общепринятая процедура определения коэффициентов уравнения (3.15) состоит в применении метода наименьших квадратов (МНК), с помощью которого находят оценки коэффициентов А и В уравнения (3.15). Обозначим эти оценки малыми буквами a и b соответственно. Предполагая, что студентам МНК известен, напомним лишь конечные результаты для случая, когда случайные ошибки имеют равные дисперсии во всех сериях опытов:
где n - в нашем случае это число серий опытов (режимов), из которых состоял эксперимент (для эксперимента 1 максимальное значение n =6, но может быть и меньшим, если задаются не все режимы). Эти оценки можно теперь использовать для построения модели, позволяющей предсказывать Т по данному значению I:
Прямая линия, задаваемая уравнением (3.20), называется прямой линейной регрессии Т на I. Наш случай может иметь отличие, заключающееся в том, что с.к.о. времени реакции различных серий опытов могут существенно отличаться друг от друга. При этом вышеизложенные формулы должны быть скорректированы. В этом случае вместо того, чтобы минимизировать сумму квадратов ошибок оценок, как это делалось в обычном МНК, следует "взвешивать" каждый член этой суммы, умножая его на величину, обратную дисперсии соответствующей случайной величины. Это придает больший вес тем наблюдениям, ошибки которых оказываются меньше, что интуитивно кажется вполне разумным. Такая процедура называется взвешенным методом наименьших квадратов. Введем в рассмотрение веса:
где Доказано, что наилучшие оценки величин a и b равны:
Здесь n - число выполненных серий опытов, Ii и t i - количество информации и среднее время реакции в i -ой серии опытов (для эксперимента 1 имеем n≤6). Итак, в случае разных дисперсий времени реакции (ВР) для построения линейной модели связи между ВР и количеством информации следует использовать взвешенный МНК (формулы 3.21-3.25). Исходными данными для него являются предварительно вычисленные средние значения ВР t i и их дисперсии В случае, если все дисперсии ВР практически совпадают, следует использовать формулы (3.16)-(3.19) с учетом тех же замечаний. Из-за ограниченного статистического материала коэффициенты закона Хика a и b определяются с большей или меньшей точностью, что позволяет говорить о "трубке точности", которая с некоторой доверительной вероятностью определяет достоверность полученной линейной модели. Оценим точность коэффициентов a и b, определяемых формулами (3.16) и (3.17). В предположении о нормальности величины времени реакции Т при данном количестве информации I оценки a и b являются несмещенными оценками А и В соответственно. Их выборочные распределения связаны с t-распределением Стьюдента. Доверительные интервалы для этих коэффициентов определяются следующими соотношениями:
Здесь и ниже величина
Величина Согласно модели Хика каждому конкретному значению информации I = I o соответствует определенное значение времени реакции Т. Доверительный интервал оценки величины Т для заданного I = I o определяется формулой:
Величины, входящие в формулу (3.29), определены выше. Таблица 1. Значения t-распределения Стьюдента для доверительной вероятности Р=0,95 и данном числе степеней свободы f
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-06; просмотров: 211; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.190.107 (0.01 с.) |

 , (3.16),
, (3.16), 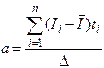 , (3.17)
, (3.17)
 (3.18),
(3.18),  , (3.19)
, (3.19) . (3.20)
. (3.20) , (3.21)
, (3.21)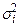 - дисперсия среднего значения времени реакции t i, вычисленного по результатам i -ой серии опытов.
- дисперсия среднего значения времени реакции t i, вычисленного по результатам i -ой серии опытов. ; (3.22),
; (3.22),  ;
;  ; (3.24)
; (3.24)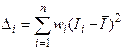 . (3.25)
. (3.25) ; (3.26),
; (3.26),  . (3.27)
. (3.27) является выборочным стандартным отклонением, определяющим отклонение значения среднего времени реакции t i от значения ВР, предсказанного формулой
является выборочным стандартным отклонением, определяющим отклонение значения среднего времени реакции t i от значения ВР, предсказанного формулой  . Это стандартное отклонение (по определению - это с.к.о. со знаком плюс) вычисляется по следующей формуле:
. Это стандартное отклонение (по определению - это с.к.о. со знаком плюс) вычисляется по следующей формуле: . (3.28)
. (3.28) является параметром распределения Стьюдента для числа степеней свободы f= n -2. Она находится из таблицы распределения Стьюдента для заданной доверительной вероятности. Обычно берут 95-процентную доверительную вероятность (или, что то же самое, уровень значимости 0,05). Отметим, что в данном случае следует брать из таблиц значение t, соответствующее двустороннему критерию значимости (соответствующая таблица приведена ниже).
является параметром распределения Стьюдента для числа степеней свободы f= n -2. Она находится из таблицы распределения Стьюдента для заданной доверительной вероятности. Обычно берут 95-процентную доверительную вероятность (или, что то же самое, уровень значимости 0,05). Отметим, что в данном случае следует брать из таблиц значение t, соответствующее двустороннему критерию значимости (соответствующая таблица приведена ниже). . (3.29)
. (3.29)


