
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Реакция выбора как информационный процессСодержание книги Поиск на нашем сайте
Одной из простейших форм информационной деятельности человека является реакция выбора. Испытуемому в соответствии с некоторым законом предъявляются последовательно один за другим стимулы, принадлежащие определенному множеству, и он должен по возможности быстрее произвести необходимые действия. Основными показателями работы оператора является время его реакции и характер допускаемых ошибок. Исследование реакции выбора имеет большое прикладное значение, поскольку выбор из нескольких альтернатив можно рассматривать как упрощенную модель деятельности оператора систем управления, где важным аспектом производительности является скорость передачи информации. Выше уже упоминалось, что реакция выбора является сенсомоторной реакцией, и рассматривались основные особенности таких реакций. Время реакции обычно обозначают через ВР или Т. ВР выбора представляет сумму нескольких составляющих, необходимых для возбуждения рецептора предъявляемым стимулом [3]: передача афферентных (от лат. "передавать в мозг") сигналов в мозг; восприятия и интерпретации этих сигналов; выбора соответствующей реакции; передачи к мускулам эфферентных (лат. "передавать из мозга") сигналов; по крайней мере начала мускульной реакции. Первые работы по применению теории информации для описания результатов измерений времени реакции человека в ситуации выбора были выполнены в начале 50-х годов английским психологом У.Хиком и американскими психологами Г.Миллером и Р,Хайманом. Эти работы базировались на результатах, полученных Меркелем еще в 80- Е годы прошлого столетия. Меркель установил, что средняя скорость, с которой человек может реагировать на последовательность беспорядочных сигналов К различных типов (при условии, что на каждый тип сигнала он должен реагировать по-разному) монотонно уменьшается с возрастанием К. Подтверждающие этот факт опыты по определению среднего ВР проводились много раз и всегда приводили к одним и тем же результатам. Наиболее обычная постановка их заключалась в том, что на стенке перед испытуемым через определенное время вспыхивала одна из К лампочек или появлялась одна из К цифр. В зависимости от номера сигнала испытуемый должен был нажать одну из К кнопок, на которых заранее лежали его пальцы, или же произвести одно из К заранее назначенных действий. Специальное устройство при этом отмечало время, проходящее между появлением сигнала и реакцией на него испытуемого. Зависимость получаемого среднего значения ВР от числа К изучалась.
Естественно, что среднее ВР можно также рассматривать как определенную меру "степени неопределенности" ожидаемого сигнала: чем больше неопределенность в исходе имеет место, тем больше требуется времени на уяснение того, какой именно сигнал был подан. Имеющиеся опыты показывают [5], что среднее ВР растет с увеличением числа К различных типов сигнала примерно как Исходя из этих данных, можно было бы предположить, что среднее ВР во всех случаях определяется энтропией опыта А, состоящего в подач е сигнала. Отсюда следует, что уменьшение степени неопределенности путем замены равновероятных сигналов неравновероятными должно на столько же уменьшить среднее ВР, на сколько оно уменьшается при уменьшении числа используемых типов сигналов, приводящем к такому же изменению энтропии Н(А). Это утверждение было подтверждено экспериментально. На рис.2 темными квадратами отмечены результаты 8 опытов (проведенные тем же испытуемым, что и раньше), в которых К лампочек (где К равнялось 2, 4, 6 или 8) зажигались с разными относительными частотами
Как видно из рис.2, темные квадратики с большой точностью укладываются на ту же прямую, что и кружки. Следовательно, энтропия Н(А) действительно является именно той мерой "степени неопределенности" исхода опыта, которая решающим образом определяет среднее время, требуемое для определения реакции на появившийся сигнал. С психологических позиций можно дать следующее объяснение изменения ВР при изменении относительной частоты различных сигналов. Вероятность появления сигнала можно трактовать как показатель психологической неожиданности его появления. Чем реже появляется сигнал, тем большая неопределенность снимается с его появлением, а следовательно, с этим сигналом воспринимается и большая информация. Однако к восприятию редких сигналов организм подготовлен хуже, чем к восприятию частых, к встреч е с которыми уже возникают навыки. Поэтому сигналы, поступающие чаще, т. е. с более высокой вероятностью, и несущие меньшую информацию, воспринимаются быстрее, чем редкие, но более информативные сигналы. Психологи считают, что большая скорость реагирования на более вероятные сигналы в какой-то мере обусловлена и физиологическими факторами - повышением возбудимости нервных структур от часто поступающих сигналов. Как отмечалось выше, если много раз производить пару опытов А и В так, чтобы опыт В следовал за опытом А, то условная энтропия H(B/A) будет характеризовать ту среднюю степень неопределенности исхода опыта В, которая остается после того, как становится известен исход предшествующего опыта А. В рассмотренных выше опытах по определению ВР всегда производилась целая серия подач сигнала, причем, перед каждой из них испытуемый знал, какие сигналы ему подавались ранее. Поэтому степень неопределенности подаваемого сигнала здесь равна условной энтропии соответствующего опыта при условии, что исходы всех предыдущих опытов (т. е. предыдущих подач сигналов) являются известными. В описанных опытах последовательные подачи сигналов всегда выбирались независимыми друг от друга. Поэтому в этих опытах условная энтропия опыта А совпадала с его безусловной энтропией Н(А). Однако, если ВР действительно определяется энтропией сигнала, то из сказанного выше должно следовать, что изменение степени неопределенности при помощи введения зависимости между последовательными подачами сигналов должно оказать то же самое влияние на изменение среднего ВР, как такое же изменение степени неопределенности при помощи изменения относительных частот этих сигналов. На рис. 2 приведены на качественном уровне результаты экспериментальной проверки этого утверждения. Здесь светлыми квадратиками обозначены результаты 8 опытов, проведенных над тем же испытуемым, что и раньше. В этих опытах требовалось по-разному реагировать на зажигание каждой из К лампочек (опыт В; число К принимало значения 2, 3, 4, 5, 8), зажигавшихся в среднем с одинаковой частотой P=1/K, но так, что частота зажигания каждой лампочки существенно зависела от того, какая лампочка зажглась непосредственно перед ней (опыт А). В отличии от предыдущих случаев на рис. 2 по оси абсцисс для данного случая откладывались значения условной энтропии, определяемой формулой (1.8):
На рис. 2 светлые квадратики с большой точностью попали на ту же прямую. Это показывает, что условная энтропия H(B/A) действительно является той степенью неопределенности, которая определяет ВР человека на исход опыта.
Во всех трех рассмотренных опытах испытуемый не имел ограничений по времени на осуществление реакции выбора. Его реакция была практически безошибочной, т. е. он имел возможность полностью устранить неопределенность и, следовательно, полностью воспринять входную информацию. Приравняв энтропию Н(А) к средней информации I(A,A), мы можем дать следующее истолкование результатам этих экспериментов. Согласно этим результатам среднее ВР возрастает пропорционально средней информации, содержащейся во входном сигнале. инач е говоря, можно предположить, что передача сообщений в живом организме во многих случаях происходит так, что за одинаковое время в среднем передается одинаковое количество информации. Из сделанного предположения вытекает простое следствие, которое можно проверить экспериментально. Пусть при проведении опыта мы заставляем испытуемого реагировать очень быстро (быстрее, чем он может уяснить себе какой сигнал появился). Например, рассматриваемые сигналы состоят в зажигании одной из К лампочек и требуется при зажигании i -той лампочки нажать i -тую кнопку. Время Т следования сигналов друг за другом (время экспозиции или предъявления сигнала) в данном случае практически совпадает со временем реакции оператора, т. е. Т=ВР. Очевидно, что при уменьшении Т испытуемый будет все чаще с чаще ошибаться (например, нажимать не ту кнопку). Это означает, что из-за необходимости очень быстро реагировать он оказывается не в состоянии полностью воспринять информацию, заключенную в появлении определенного сигнала. Если время Т не слишком мало, то некоторую полезную информацию испытуемый успевает получить. Его реакция не будет совершенно беспорядочной. В среднем на i -ю лампочку он будет нажимать i -ю кнопку чаще, чем какую-либо другую. Опыт В, состоящий в нажимании одной из К кнопок, здесь будет содержать определенную информацию об опыте А, состоящем в зажигании одной из К лампочек. Это средняя информация, которую испытуемый способен воспринять за время Т. Согласно предположению эта информация должна зависеть от ВР, как зависит от ВР энтропия Н(А) в том случае, когда ВР определяется как наименьшее время, достаточное для безошибочной реакции. Проверка последнего была проведена У.Хиком. Результаты на качественном уровне приведены на рис. 3. Крестиками обозначены результаты опыта, в котором использовались 10 лампочек, зажигавшихся с одинаковой частотой, но ВР (напоминаем, что здесь ВР=Т) заранее устанавливалось столь малым, что реакция испытуемого в ряде случаев оказывалась ошибочной. Введем обозначения:
В - опыт, заключающийся в нажатии одной из 10 кнопок, А - опыт, заключающийся в появлении одного из 10 сигналов, Т - время реакции, равное времени предъявления сигнала, N - число испытаний с одним и тем же Т,
Очевидно, что сумма всех
Ясно, что вероятности 10 исходов опыта А можно приближенно рассчитать так:
Вероятности 10 исходов опыта В будут равны:
Сложный опыт AB здесь будет иметь 102=100 различных исходов, вероятности которых приближенно равны соответствующим частотам:
Отсюда для энтропии опытов A, B и AB получаются выражения
Формулы (1.11)-(1.13) позволяют приближенно подсчитать энтропии по экспериментально определенным числам H(A/B)=H(A,B)-H(B) (1.14) I(A,B)=H(A)-H(A/B) (1.15) Это значение количества информации и откладывалось по оси абсцисс на рис. 3 при нанесении крестиков. Как видно из рис. 3, крестики укладывались на ту же прямую, на которую уложились результаты (кружки) из предыдущего эксперимента. Как и ранее использовались равновероятные сигналы и не было ограничений на ВР. Таким образом, получено подтверждение линейной зависимости времени реакции выбора (ВР) именно от информации, содержащейся в сигнале. Как уже упоминалось, время реакции будем обозначать через ВР или Т. Эта зависимость записывается: T=ВР = aI+b, (1.16) Зависимость (1.16) называют законом Хика. Таким образом, в рассмотренной задач е испытуемые действовали как информационные каналы с ограниченной пропускной способностью, для которых взаимодействие между временем и точностью обусловлено постоянной скоростью передачи информации в битах в секунду. Согласно (1.16) основная информационная модель, описывающая требуемое для реагирования время, состоит в том, что Следует иметь ввиду, что хотя модель, описываемая законом Хика, является очень полезной для осмысления информационной производительности человека-оператора, ее применимость ограничена в силу зависимости максимальной скорости передачи информации от специфических особенностей задачи, т. е. рассмотренная модель не может быть адекватна всем процессам передачи информации в живом организме.
|
|||||||||
|
Последнее изменение этой страницы: 2016-06-06; просмотров: 322; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.195.229 (0.012 с.) |

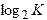 , т. е. как шенноновская энтропия H(A) опыта А, состоящего в подач е сигнала. Для примера на рис.2 приведены графики, на качественном уровне отражающие некоторые результаты из работы Хаймана. Кружками отмечены результаты 8 опытов, состоящих в определении среднего ВР, необходимого испытуемому, чтобы указать, какая из К лампочек (число К менялось от 1 до 8) зажглась. Это среднее время определялось из большого числа серий зажиганий, в каждой из которых частоты зажиганий всех лампочек были одинаковыми. Причем, предварительно испытуемый специально тренировался в подобных условиях. По оси ординат отложено среднее ВР, а по оси абсцисс - величина
, т. е. как шенноновская энтропия H(A) опыта А, состоящего в подач е сигнала. Для примера на рис.2 приведены графики, на качественном уровне отражающие некоторые результаты из работы Хаймана. Кружками отмечены результаты 8 опытов, состоящих в определении среднего ВР, необходимого испытуемому, чтобы указать, какая из К лампочек (число К менялось от 1 до 8) зажглась. Это среднее время определялось из большого числа серий зажиганий, в каждой из которых частоты зажиганий всех лампочек были одинаковыми. Причем, предварительно испытуемый специально тренировался в подобных условиях. По оси ординат отложено среднее ВР, а по оси абсцисс - величина  . При этом мы видим, что все 8 кружочков довольно точно укладываются на одну линию.
. При этом мы видим, что все 8 кружочков довольно точно укладываются на одну линию. . Причем, предварительно испытуемый тренировался на сериях зажиганий с этими частотами. Здесь снова по оси ординат отложено среднее ВР, а по оси абсцисс - энтропия, определяемая по формуле (1.1).
. Причем, предварительно испытуемый тренировался на сериях зажиганий с этими частотами. Здесь снова по оси ординат отложено среднее ВР, а по оси абсцисс - энтропия, определяемая по формуле (1.1).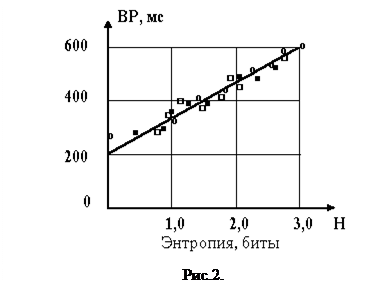
 (1.8)
(1.8)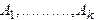 - исходы опыта А.
- исходы опыта А. - число случаев, в которых в ответ на зажигание i -той лампочки была нажата j -ая кнопка (здесь i, j меняются от 1 до 10).
- число случаев, в которых в ответ на зажигание i -той лампочки была нажата j -ая кнопка (здесь i, j меняются от 1 до 10).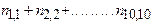 .
.
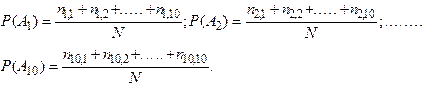 (1.9a)
(1.9a) (1.9b)
(1.9b) (1.10)
(1.10)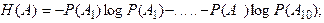 (1.11)
(1.11) (1.12)
(1.12) (1.13)
(1.13)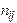 . После этого можно найти условную энтропию по формуле:
. После этого можно найти условную энтропию по формуле: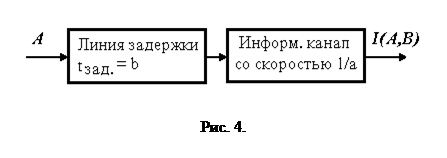 человек-оператор действует как совокупность линии задержки и канала с ограниченной скоростью передачи информации (рис. 4). Коэффициенты, входящие в уравнение (1.16), имеют следующий физический смысл: b - это время латентного периода; 1/a - скорость передачи информации по каналу. Однако экспериментально измеренная величина b оказывается несколько больше латентного периода, если она определяется как время простой сенсомоторной реакции (см. рис. 1), например, реакции на зажигание в произвольный момент времени одной и той же лампочки.
человек-оператор действует как совокупность линии задержки и канала с ограниченной скоростью передачи информации (рис. 4). Коэффициенты, входящие в уравнение (1.16), имеют следующий физический смысл: b - это время латентного периода; 1/a - скорость передачи информации по каналу. Однако экспериментально измеренная величина b оказывается несколько больше латентного периода, если она определяется как время простой сенсомоторной реакции (см. рис. 1), например, реакции на зажигание в произвольный момент времени одной и той же лампочки.


