
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение характеристик человека-оператора как дискретного канала передачи информацииСодержание книги
Поиск на нашем сайте
I(A,A) = I(A,B) = H(A) (1.17) Этот случай соответствует эксперименту по вынужденному выбору с неограниченным временем предъявления стимула, когда оператор имеет возможность правильно воспринять всю информацию. Когда время предъявления стимула ограничено долями секунды, оператор начинает работать как дискретный канал с потерей информации и с шумом. В этом случае количество передаваемой оператором информации может быть подсчитано тремя способами (см. предыдущие разделы). При этом учтем особенности нашего эксперимента, которые состоят в следующем. Число исходов опыта A (появление входных сигналов) равно К. Оператор должен отвечать на каждый тип входного сигнала своей реакцией, т. е. число правильных реакций равно К. Но из-за дефицита времени оператор будет ошибаться и отвечать неверными реакциями, к которым относятся как реакции из заданного множества (например, нажатие не той кнопки), так и реакции из дополнительного множества, число которых в общем случае может быть как угодно велико. К этим неверным реакциям из дополнительного множества относится и пропуск сигнала, например, реакция в виде ненажатия кнопки при появлении входного сигнала. Проблема, стоящая перед экспериментатором, состоит только в том, чтобы уметь регистрировать все множество неверных реакций. Таким образом, число исходов опыта B (ответные реакции оператора) может значительно превышать число входных сигналов К. Вообще говоря, возможен и противоположный случай, когда число исходов опыта B меньше числа К и в предельном случае равно 1 (например, оператор пропускает все сигналы). Однако при нормальной организации лабораторных исследований такой вариант маловероятен. В данной работе рассматривается простейший случай, когда дополнительное множество неверных реакций состоит лишь из одного члена, соответствующего пропуску сигнала. Причем под пропуском сигнала мы будем подразумевать не только ненажатие кнопки, но и несвоевременное нажатие кнопки (после исчезновения сигнала). Дальнейшее рассмотрение проведем на примере, когда ответные реакции оператора будут заключаться в нажатии лишь 9 клавиш дополнительной цифровой клавиатуры ЭВМ, т.е. число исходов опыта A или число входных сигналов будет равно К=9. Следовательно, число исходов опыта B или число ответных реакций в нашем эксперименте будет М=К+1=10. Для этого конкретного случая рассмотрим математические выражения, которые определяют три способа вычисления количества информации. Первый способ Выше для подсчета количества информации была получена формула (1.15), которую с учетом формулы (1.14) можно переписать в виде I(A,B) = H(A) + H(B) - H(A,B). (1.18) Входящие в нее энтропии определяются следующим образом:
Таким образом, для расчета количества воспринимаемой оператором информации по формуле (1.18) необходимо уметь вычислять вероятности опытов по экспериментальным данным, а по ним - соответствующие энтропии. Второй способ В канале может присутствовать шум, т. е. ложная информация, которая прибавляется к передаваемой информации (см. рис. 4). В результате выходная информация, характеризуемая выходной энтропией Н(В), отличается от передаваемой информации на величину H(B/A) = H(B) - I(A,B). (1.22)
Из формулы (1.22) количество информации может быть рассчитано следующим образом: I(A,B) = H(B) - H(B/A), (1.24) где Н (В) можно рассчитать по формуле (1.20). Третий способ Как следует из диаграммы дискретного информационного канала (рис. 4), переданная информация равна разности между входной информацией, определяемой энтропией Н(А), и потерями информации, определяемыми условной энтропией H(A/B) H(A/B) = H(A) - I(A,B), I(A,B) = H(A) - H(A/B). (1.25) Входная энтропия Н(А) определяется выражением (1.19). Потери информации определяются условной энтропией H(A/B), которая характеризует остаточную (апостериорную) неопределенность входного сообщения при известном сообщении на выходе (т. е. после проведения опыта). По аналогии с (1.23) для этой условной энтропии можно получить:
|
||||
|
Последнее изменение этой страницы: 2016-06-06; просмотров: 218; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.108.8 (0.006 с.) |

 В данной лабораторной работе, так же как и в опытах Хика и Хаймена, производится регистрация времени реакции ВР оператора при решении им задач выбора разной сложности. Отличие состоит в том, что эксперимент проводится на ЭВМ. Для построения зависимости ВР от количества обработанной человеком дискретной информации необходимо уметь вычислять эту информацию по экспериментальным данным. Для этого вкратце рассмотрим дискретный информационный канал (рис. 5). Входная информация определяется энтропией H(A). Следовательно, в идеальном канале, где нет потерь информации и шума, переданная информация I(A,A) равна входной энтропии H(A)
В данной лабораторной работе, так же как и в опытах Хика и Хаймена, производится регистрация времени реакции ВР оператора при решении им задач выбора разной сложности. Отличие состоит в том, что эксперимент проводится на ЭВМ. Для построения зависимости ВР от количества обработанной человеком дискретной информации необходимо уметь вычислять эту информацию по экспериментальным данным. Для этого вкратце рассмотрим дискретный информационный канал (рис. 5). Входная информация определяется энтропией H(A). Следовательно, в идеальном канале, где нет потерь информации и шума, переданная информация I(A,A) равна входной энтропии H(A) , (1.19)
, (1.19) , (1.20)
, (1.20) , (1.21)
, (1.21)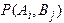 - совместная вероятность исходов Ai, Bj.
- совместная вероятность исходов Ai, Bj.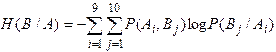 . (1.23)
. (1.23) , (1.26)
, (1.26)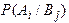 - условная вероятность опыта Ai из входного множества А при условии, что известен исход на выходе Bj из выходного множества В.
- условная вероятность опыта Ai из входного множества А при условии, что известен исход на выходе Bj из выходного множества В.


