
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закон распределения случайной величиныСодержание книги
Поиск на нашем сайте
Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. Про случайную величину будем говорить, что она подчинена данному закону распределения. Формой задания закона является таблица
Такую таблицу мы будем называть рядом распределения случайной величины X. Графическое изображение ряда распределения называется многоугольником распределения
x1 x2 x3 … xn Многоугольник распределения - также одна из форм закона распределения. 15. Интегральная Функция распределения Св и ее св-ва: Мы рассмотрели закон распределения дискретной случайной величины. Для непрерывной случайной величины такую характеристику построить нельзя. Непрерывная случайная величина имеет бесчисленное множество возможных значений, сплошь заполняющих некоторый промежуток (несчетное множество). Для непрерывной случайной величины не существует ряда распределения, как он существует для дискретной величины. Но различные области возможных значений случайных величин все же не является одинаково вероятными, и для непрерывной величины существует распределение вероятностей, хотя и не в том смысле, как для прерывной. Для количественной характеристики, этого распределения вероятностей удобно воспользоваться не вероятностью события Функцию распределения
1. Проиллюстрируем эти свойства с помощью геометрической интерпретации. Б. рассм-ть СВ Тогда Очевидно, при этом вероятность того, что Неограниченно перемещаем точку Из полученного только что равенства имеем:
Построим график функции распределения
Зная ряд распределения случайной величины легко построить функцию распределения этой величины. Действительно, 16. Плотность распределения CВ и ее св-ва Пусть имеется непрерывная случайная величина
т.е. приращение функции распределения на этом участке. Рассмотрим отношение этой вероятности к длине участка, т.е. среднюю вероятность, приходящуюся на единицу длины на этом участке, и будем приближать Dx®0. В пределе получим производную от функции распределения Функция
Плотность распределения так же, как и функция распределения есть одна из
форм закона распределения. Функции распределения существует только для непрерывных случайных величин. Рассмотрим непрерывную случайную величину
Выразим вероятность попадания величины
Формула (*) выражает плотность распределения через функцию распределения. Зададимся обратной задачей: выразить функцию распределения через плотность. По определению
откуда Св-ва: 1. Плотность распределения есть неотрицательная функция 2. Интеграл в бесконечных пределах от плотности распределения равен 1:
3. Действительно, Геометрически все основные свойства плотности распределения означают, что - кривая лежит не ниже оси абсцисс; - полная площадь, ограниченная кривой распределения и осью абсцисс, равна 1.
Пример 1. Функция распределения непрерывной случайной величины
1. Найти плотность распределения f(x). 2. Найти вероятность попадания величины
Решение. Плотность распределения выражается формулой:
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 349; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.132.71 (0.01 с.) |


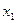












 p1
p1 xi
xi , а вероятностью события
, а вероятностью события  , где
, где  – некоторая текущая переменная. Вероятность этого события есть некоторая функция от
– некоторая текущая переменная. Вероятность этого события есть некоторая функция от  . Эта функция называется функцией распределения случайной величины
. Эта функция называется функцией распределения случайной величины  ,
,  .
. ,
,  ;
; ;
;  .
. . Аналогично перемещая точку
. Аналогично перемещая точку  , т. к. событие
, т. к. событие  . Рассмотрим событие
. Рассмотрим событие  =
= 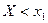 и
и  =
=  .
.  Æ,
Æ,  . Применим теорему сложения для несовместных событий
. Применим теорему сложения для несовместных событий  или
или  , т.е.
, т.е.  .
. . Отсюда следует, что какой бы ни был задан полуинтервал
. Отсюда следует, что какой бы ни был задан полуинтервал  , зная
, зная  . Если вероятность оказалась, например, равной нулю, то это значит, что на данном промежутке нет возможных значений
. Если вероятность оказалась, например, равной нулю, то это значит, что на данном промежутке нет возможных значений  F(X)
F(X)
 1
1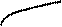

 0 X
0 X , где неравенство
, где неравенство  под знаком суммы указывает, что суммирование распространяется на все те значения
под знаком суммы указывает, что суммирование распространяется на все те значения 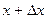 .
.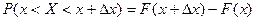 ,
, Обозначим
Обозначим  . (*)
. (*) - производная функции распределения, характеризует как бы плотность, с которой распределяются значения случайной величины в данной точке. Эта функция называется плотностью распределения (плотностью вероятности) непрерывной случайной величины
- производная функции распределения, характеризует как бы плотность, с которой распределяются значения случайной величины в данной точке. Эта функция называется плотностью распределения (плотностью вероятности) непрерывной случайной величины 


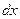 , примыкающий к точке
, примыкающий к точке  .
.

 до
до  через плотность распределения. Очевидно, оно равно
через плотность распределения. Очевидно, оно равно .
. ,
, .
. , что вытекает из того, что
, что вытекает из того, что  , что следует из формул
, что следует из формул  и
и  .
.
 .
. Вероятность того, что случайная величина
Вероятность того, что случайная величина 





