
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Биномиальный закон распределенияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Случайная величина Если проводятся независимые испытания, в каждом из которых событие Приведем таблицу распределения биномиальной случайной величины
Проверим корректность определения случайной величины
Здесь Найдем математическое ожидание и дисперсию биномиальной случайной величины
Очевидно, что
Тогда
Итак, Закон распределения Пуассона Случайная величина
где
Данное выше определение корректно. Действительно,
Найдем математическое ожидание и дисперсию данной случайной величины
Таким образом, если
Согласно теореме Пуассона, распределение Пуассона – это предельный случай биномиального распределения, когда Равномерный закон распределения Непрерывная случайная величина, которая принимает значения только на сегменте [a,b] с постоянной плотностью распределения, называется распределенной по равномерному закону. Из определения следует, что плотность распределения определяется равенством
и должна удовлетворять двум требованиям: 1) 2)
Найдем математическое ожидание и дисперсию случайной величины, распределенной равномерно на сегменте [a,b]:
Следовательно, Равномерный закон распределения применяется при работе с округленными числами. Например, если число округлено до целого, то ошибка округления Показательный закон распределения Непрерывная случайная величина X, которая принимает только неотрицательные значения с плотностью распределения
называется распределенной по показательному закону с параметром
т.е. приведенное определение корректно. Функция распределения показательно распределенной случайной величины X имеет вид:
Найдем математическое ожданиеи дисперсию случайной величины, распределенной по показательному закону.
Поэтому Нормальный закон распределения Случайная величина X распределена по нормальному закону, если плотность рапределения определяется по формуле
где
Так как
таким образом, приведенное выше определение корректно. Математическое ожидание нормального закона распределения. Найдем математическое ожидание и дисперсию случайной величины X, распределенной по нормальному закону с параметрами
Проведем замену в этом интеграле
(интеграл от нечетной функции равен нулю по симметричному относительно начала координат промежутку).
|
||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 818; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.249.191 (0.007 с.) |

 , которая принимает значение
, которая принимает значение  с вероятностью
с вероятностью 
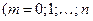
 , называется распределенной по биномиальному закону.
, называется распределенной по биномиальному закону. может наступить с одной и той же вероятностью
может наступить с одной и той же вероятностью  , то число наступлений события
, то число наступлений события  испытаниях и есть случайная величина
испытаниях и есть случайная величина 



 .
. - вероятность того, что событие
- вероятность того, что событие  - наступит один раз;
- наступит один раз;  - два раза и т.д. или, наконец,
- два раза и т.д. или, наконец,  - это число наступлений события
- это число наступлений события  ом испытании. Тогда распределение случайной величины
ом испытании. Тогда распределение случайной величины 
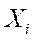 ,
,  - независимые случайные величины и их сумма
- независимые случайные величины и их сумма  - это случайная величина
- это случайная величина  ,
,  ,
,  .
. ,
,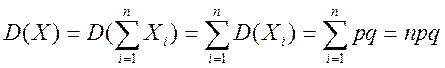 .
. ,
,  ,
, 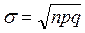 .
. ,
, ,
,  , называется распределенной по закону Пуассона с параметром
, называется распределенной по закону Пуассона с параметром  . Этот закон может быть записан в виде следующей таблицы:
. Этот закон может быть записан в виде следующей таблицы:




 и
и .
. .
. ,
,


 распределено по закону Пуассона с параметром
распределено по закону Пуассона с параметром  .
. ,
,  и
и  . По закону Пуассона распределены числа так называемых редких явлений (например, число рождения четверней, число вызовов на АТС, поступивших в течение минуты, число несчастных случаев на производстве и т.д.).
. По закону Пуассона распределены числа так называемых редких явлений (например, число рождения четверней, число вызовов на АТС, поступивших в течение минуты, число несчастных случаев на производстве и т.д.).

 ,
,  ,
,  ,
,  . Таким образом
. Таким образом Найдем функцию распределения данной случайной величины. Известно, что
Найдем функцию распределения данной случайной величины. Известно, что  , Тогда согласно формуле выше, получим
, Тогда согласно формуле выше, получим


 ,
,  ,
, 
 распределена равномерно на
распределена равномерно на  .
. ,
, 
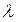 . Так как
. Так как ,
,





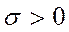 и а – параметры распределения.
и а – параметры распределения. и
и  [введем замену
[введем замену  ]
]
 и а:
и а:
 , тогда
, тогда  ,
,  , пределы интегрирования не меняются и, следовательно,
, пределы интегрирования не меняются и, следовательно,



