
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Генеральная и выборочная совокупности.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
При этом подлежащая изучению статистическая совокупность, из которой производится отбор части единиц, называется генеральной совокупностью. Отобранная из генеральной совокупности некоторая часть единиц, подвергающаяся обследованию, называется выборочной совокупностью, или просто выборкой. Основные характеристики параметров генеральной и выборочной совокупности обозначаются определёнными символами. Символы основных характеристик параметров генеральной и выборочной совокупностей
27,28 Средняя и предельная ошибки выборки. Методы определения ошибок выборки Между характеристиками выборочной совокупности и искомыми характеристиками генеральной совокупности существует некоторое расхождение, называемое ошибкой выборки. Классификация ошибок выборки
После проведения отбора для определения возможных границ генеральных характеристик рассчитываются средняя и предельная ошибки выборки. Применение выборочного метода связано с возникновением ошибок репрезентативности, которые представляют собой разность между обобщающими показателями генеральной выборочной совокупностей. Выборочная совокупность может формироваться разными методами. Может иметь место индивидуальный отбор (когда отбирается каждый раз одна единица совокупности) или серийный (отбор производится сериями, гнездами, упаковками и т.п., и в них обследуются все единицы).После обследования отобранные единицы могут быть возвращены в генеральную совокупность, где имеют одинаковую со всеми единицами вероятность вновь попасть в выборку – повторный отбор либо могут не участвовать в дальнейшем отборе – бесповторный отбор. Отбор может быть произведен собственно-случайным способом, механическим и типическим. При собственно-случайной выборке отбор производится жеребьевкой. Механический способ отбора используется в тех случаях, когда имеется возможность составить список единиц совокупности в порядке их естественного расположения (по алфавиту, по времени появления и т.п.). Отбор осуществляется механически – через определенный интервал.При типическом отборе обследуемая генеральная совокупность подразделяется на типические группы, из которых затем отбирается определенное число единиц так, чтобы сохранить в выборе структуру генеральной совокупности. Ошибки репрезентативности могут быть рассчитаны как средняя или стандартная (μ) и максимальная с определенной вероятностью – предельная ( Средняя ошибка типического отбора. При повторном методе отбора При бесповторном методе отбора где Средняя ошибка при отборе сериями (серийная выборка). При повторном отборе При бесповторном отборе где Предельная ошибка выборки (
Коэффициент доверия зависит от вероятности, с которой можно гарантировать определенные размеры предельной ошибки:
Обобщающая характеристика в генеральной совокупности (
Приведенные выше формулы ошибок выборки позволяют заранее рассчитать тот объем выборки (репрезентативная выборка), при котором отклонение выборочных показателей от генеральных не превысит заданных размеров, гарантируемых с определенной вероятностью. Репрезентативная выборка (n). При повторном отборе При бесповторном отборе При определении необходимой численности выборки для определения дисперсии используют данные предыдущих обследований. При полном отсутствии каких-либо данных о вариации задают максимальную величину дисперсии: для количественного признака
Для альтернативного признака Малой выборкой называют выборку, объем которой не превышает 20 единиц ( Средняя ошибка малой выборки (
Для увязки средней и предельной ошибок малой выборки используется коэффициент распределения Стьюдента (псевдоним В. Госсета)
где Вероятность того, что характеристика генеральной совокупности не выйдет за пределы
Последняя формула применяется для нахождения пределов генеральной средней с заданной вероятностью.
29 Методы определения тесноты связи корреляционной связи (параметрические и непараметрические методы оценки). Корреляционная связь - это связь, где воздействие отдельных факторов проявляется только как тенденция (в среднем) при массовом наблюдении фактических данных. Примерами корреляционной зависимости могут быть зависимости между размерами активов банка и суммой прибыли банка, ростом производительности труда и стажем работы сотрудников. Методы оценки тесноты связи подразделяются на корреляционные (параметрические) и непараметрические. Параметрические методы основаны на использовании, как правило, оценок нормального распределения и применяются в случаях, когда изучаемая совокупность состоит из величин, которые подчиняются закону нормального распределения. На практике это положение чаще всего принимается априори. Собственно, эти методы – параметрические – и принято называть корреляционными. Непараметрические методы не накладывают ограничений на закон распределения изучаемых величин. Их преимуществом является и простота вычислений. Наиболее простым вариантом корреляционной зависимости является парная корреляция, т.е. зависимость между двумя признаками (результативным и факторным или между двумя факторными). Математически эту зависимость можно выразить как зависимость результативного показателя у от факторного показателя х. Связи могут быть прямые и обратные. В первом случае с увеличением признака х увеличивается и признак у, при обратной связи с увеличением признака х уменьшается признак у. Важнейшей задачей является определение формы связи с последующим расчетом параметров уравнения, или, иначе, нахождение уравнения связи (уравнения регрессии). Могут иметь место различные формы связи: прямолинейная
криволинейная в виде: параболы второго порядка (или высших порядков)
гиперболы
показательной функции
и т.д. Параметры для всех этих уравнений связи, как правило, определяют из системы нормальных уравнений, которые должны отвечать требованию метода наименьших квадратов (МНК):
Если связь выражена параболой второго порядка (
Другая важнейшая задача - измерение тесноты зависимости - для всех форм связи может быть решена при помощи вычисления эмпирического корреляционного отношения
где - Для определения степени тесноты парной линейной зависимости служит линейный коэффициент корреляции r, для расчета которого можно использовать, например, две следующие формулы:
Линейный коэффициент корреляции может принимать значения в пределах от -1 до + 1 или по модулю от 0 до 1. Чем ближе он по абсолютной величине к 1, тем теснее связь. Знак указывает направление связи: «+» - прямая зависимость, «-» имеет место при обратной зависимости. Непараметрические показатели связи В статистической практике могут встречаться такие случаи, когда качества факторных и результативных признаков не могут быть выражены численно. Поэтому для измерения тесноты зависимости необходимо использовать другие показатели. Для этих целей используются так называемые непараметрические методы. Наибольшее распространение имеют ранговые коэффициенты корреляции, в основу которых положен принцип нумерации значений статистического ряда. При использовании коэффициентов корреляции рангов коррелируются не сами значения показателей х и у, а только номера их мест, которые они занимают в каждом ряду значений. В этом случае номер каждой отдельной единицы будет ее рангом. Коэффициент корреляции рангов Спирмэна (р) основан на рассмотрении разности рангов значений результативного и факторного признаков и может быть рассчитан по формуле
где d = Nx - Ny, т.е. разность рангов каждой пары значений х и у; n - число наблюдений. Ранговый коэффициент корреляции Кендэла (
где S = P + Q. К непараметрическим методам исследования можно отнести коэффициент ассоциации Кас и коэффициент контингенции Ккон, которые используются, если, например, необходимо исследовать тесноту зависимости между качественными признаками, каждый из которых представлен в виде альтернативных признаков. Здесь а, b, c, d - частоты взаимного сочетания (комбинации) двух альтернативных признаков Коэффициент ассоциации можно расcчитать по формуле
Коэффициент контингенции рассчитывается по формуле
Нужно иметь в виду, что для одних и тех же данных коэффициент контингенции (изменяется от -1 до +1) всегда меньше коэффициента ассоциации. Если необходимо оценить тесноту связи между альтернативными признаками, которые могут принимать любое число вариантов значений, применяется коэффициент взаимной сопряженности Пирсона (КП). Коэффициент взаимной сопряженности Пирсона определяется по формуле
где
Коэффициент взаимной сопряженности изменяется от 0 до 1. Наконец, следует упомянуть коэффициент Фехнера, характеризующий элементарную степень тесноты связи, который целесообразно использовать для установления факта наличия связи, когда существует небольшой объем исходной информации. Данный коэффициент определяется по формуле
где na - количество совпадений знаков отклонений индивидуальных величин от их средней арифметической; nb - соответственно количество несовпадений. Коэффициент Фехнера может изменяться в пределах -1,0
|
||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 586; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.232.215 (0.013 с.) |



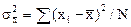



 ). Средняя ошибка выборки для собственно случайного и механического способа. При повторном методе отбора
). Средняя ошибка выборки для собственно случайного и механического способа. При повторном методе отбора 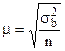 .При бесповторном методе отбора
.При бесповторном методе отбора  ,где
,где  - дисперсия выборочных данных; n – объем выборки; N – объем генеральной совокупности.
- дисперсия выборочных данных; n – объем выборки; N – объем генеральной совокупности. .
.
 - средняя из групповых вариаций в выборке по типическим группам.
- средняя из групповых вариаций в выборке по типическим группам.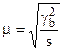 .
. ,
, - межгрупповая вариация; s – количество отобранных серий; S – количество серий в генеральной совокупности.
- межгрупповая вариация; s – количество отобранных серий; S – количество серий в генеральной совокупности. .
.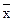 ) определяется доверительным интервалом, уточнение обобщающей характеристики выборочной совокупности (
) определяется доверительным интервалом, уточнение обобщающей характеристики выборочной совокупности ( ) на предельную ошибку выборки:
) на предельную ошибку выборки: или
или  с заданной вероятностью.
с заданной вероятностью.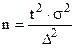 .
. .
. .
.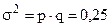 .
. ).
). ) определяется по формуле
) определяется по формуле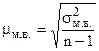 .
. ,
, - коэффициент Стьюдента, определяемый по распределению Стьюдента
- коэффициент Стьюдента, определяемый по распределению Стьюдента 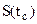 в зависимости от n.
в зависимости от n. , с распределением Стьюдента связана следующим образом:
, с распределением Стьюдента связана следующим образом: .
.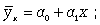
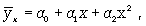

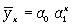 (8.4)
(8.4)
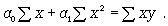 (8.5)
(8.5) ), то систему нормальных уравнений для отыскания параметров a0, a1, a2 (такую связь называют множественной, поскольку она предполагает зависимость более чем двух факторов) можно представть в виде
), то систему нормальных уравнений для отыскания параметров a0, a1, a2 (такую связь называют множественной, поскольку она предполагает зависимость более чем двух факторов) можно представть в виде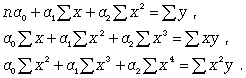 (8.6)
(8.6) :
: (8.7)
(8.7) дисперсия в ряду выравненных значений результативного показателя
дисперсия в ряду выравненных значений результативного показателя  ;
;  - дисперсия в ряду фактических значений у.
- дисперсия в ряду фактических значений у. (8.8)
(8.8)
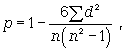 (8.9)
(8.9) ) можно определить по формуле
) можно определить по формуле (8.10)
(8.10) ; n - общая сумма частот.
; n - общая сумма частот. (8.11)
(8.11) (8.12)
(8.12)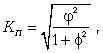 (8.13)
(8.13) - показатель средней квадратической сопряженности:
- показатель средней квадратической сопряженности:
 (8.14)
(8.14) Кф
Кф 


