
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы выравнивания рядов динамики: укрупнение интервалов, сглаживание способом скользящей средней, выравнивание по аналитическим формулам.Содержание книги
Поиск на нашем сайте
Важнейшей задачей характеристики динамики общественных явлений является выявление основной тенденции развития. Эта задача решается методами выравнивания рядов динамики, которые включают механическое выравнивание, метод скользящей средней, аналитическое выравнивание. 1) Механическое выравнивание – заключается в укрупнении интервалов и определении для укрупненного интервала среднего или суммарного значения признака. 2) Метод скользящей средней заключается в последовательном расчете средних уровней из заданного числа по порядку уровней ряда, каждый раз отбрасывая один уровень в начале и добавляя один следующий. Каждое звено скользящей средней – это уровень за соответствующий период, который относится к середине выбранного периода, если число уровней скольжения нечетное. Например, для ряда динамики, представленного уровнями у1, у2, у3, у4, у5 скольжение 3- уровневой средней будет иметь вид:
Нахождение скользящей средней по четному числу уровней несколько сложнее, так как средняя может быть отнесена к середине между двумя периодами, находящимися в середине интервала сглаживания. Чтобы ликвидировать такой сдвиг, применяют способ центрирования. Центрирование заключается в нахождении средней из двух смежных скользящих средних для отнесения полученного уровня к определенному периоду.
Центрированием получаем 3) Аналитическое выравнивание предполагает представление уровней данного ряда динамики в виде функции времени Адекватная формула развития может быть представлена прямолинейной зависимостью Проблема аналитического выравнивания сводится к определению параметров адекватной формулы развития аналогично методике определения параметров уравнения регрессии (см. п.1.8), с применением упрощенного расчета на основе переноса начала координат в середину ряда динамики, получая, таким образом, В этом случае система нормальных уравнений для нахождения параметров прямой будет иметь вид
для параболы 2го порядка
Нумерация последовательности периодов времени при нечетном числе уровней 1, 2, 3, …, n после переноса начала координат t будет …-3, -2, -1, 0, 1, 2, 3, … при четном числе уровней … -5, -3, -1, 1, 3, 5 …
22 Определение основной тенденции ряда динамики (тренд). Рассмотрим основные методы преобразования рядов динамики, позволяющие обнаружить и обосновать основную тенденцию в развитии явления. На практике наиболее распространенными методами статического изучения тренда являются: укрупнения интервала, сглаживание скользящей средней, аналитическое выравнивание. Для определения основной тенденции развития явления, достаточно устойчивой на протяжении данного периода, используют особые приемы обработки рядов динамики. Уровни ряда динамики формируются под совокупным влиянием множества длительно и кратковременно действующих факторов и в том числе различного рода случайных обстоятельств. Выявление основной закономерности изменения уровней ряда предполагает ее количественное выражение, в некоторой мере свободное от случайных воздействий. Выявление основной тенденции развития (тренда) называется в статистике также выравниванием временного ряда, а методы выявления основной тенденции - методами выравнивания. Выравнивание позволяет характеризовать особенность изменения во времени данного динамического ряда в наиболее общем виде как функцию времени, предполагая, что через время можно выразить влияние всех основных факторов. Один из наиболее простых приемов обнаружения общей тенденции развития явления - укрупнение интервала динамического ряда. Смысл приема заключается в том, что первоначальный ряд динамики преобразуется и заменяется другим, показатели которого относятся к большим по продолжительности периодам времени. Например, ряд, содержащий данные о месячном выпуске продукции, может быть преобразован в ряд квартальных данных. Вновь образованный ряд может содержать либо абсолютные величины (за укрупненные по продолжительности промежутки времени), и величины получают путем простого суммирования уровней первоначального ряда абсолютных величин, либо средние величины. При суммировании уровней или при выведении средних по укрупненным интервалам отклонения в уровнях, обусловленных случайными причинами, взаимопогашаются, сглаживаются. и более четко обнаруживается действие основных факторов изменения уровней (общая тенденция).
Выявление основной тенденции может быть осуществлено также методом скользящей средней. Для определения скользящей средней формируем укрупненные интервалы, состоящие из одинакового числа уровней. Каждый последующий интервал получаем, постепенно сдвигаясь от начального уровня динамического ряда на один уровень. Тогда первый интервал будет включать уровни у1, у2,... уm; второй - уровни у2,у3,... у m+1 и т.д. Таким образом, интервал сглаживания как бы скользит по динамическому ряду с шагом, равным единице. По сформированным укрупненным интервалам определяем сумму значений уровней, на основе которых рассчитываем скользящие средние. Полученная средняя относится к середине укрупненного интервала. Поэтому при сглаживании скользящей средней технически удобнее укрупненный интервал составлять из нечетного числа уровней ряда. Нахождение скользящей средней по четному числу уровней создает неудобство, вызываемое тем, что средняя может быть отнесена только к середине между двумя датами. В этом случае необходима дополнительная процедура центрирования средних. Нередко выбор интервала сглаживания осуществляется произвольно, однако при этом нужно учитывать количество уровней в анализируемом ряду динамики, так как при использовании приема скользящей средней сглаженный ряд сокращается по сравнению с исходным рядом на число уровней, равное (m -1). Вместе с тем, чем продолжительнее интервал сглаживания, тем сильнее усреднение, а потому выявляемая тенденция развития получается более плавной. Чаще всего интервал сглаживания может состоять из трех, пяти или семи уровней. Изучение основной тенденции развития методом скользящей средней является лишь эмпирическим приемом предварительного анализа. Рассмотренные приемы сглаживания динамических рядов (укрупнение интервала и метод скользящей средней) могут рассматриваться как важное вспомогательное средство, облегчающее применение других методов и, в частности, более строгих методов выявления тенденции. Для того чтобы представить количественную модель, выражающую общую тенденцию изменений уровней динамического ряда во времени, используется аналитическое выравнивание ряда динамики. В этом случае фактические уровни заменяются уровнями, вычисленными на основе определенной кривой. Предполагается, что она отражает общую тенденцию изменения во времени изучаемого показателя. При аналитическом выравнивании ряда динамики закономерно изменяющийся уровень изучаемого показателя оценивается как функция времени
|
||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 1437; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.234.56 (0.011 с.) |

 ;
; 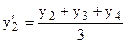 ;
;  .
. ;
; 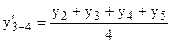 .
. .
. , называемой адекватной формулой ряда динамики или аналитическое выражение тренда.
, называемой адекватной формулой ряда динамики или аналитическое выражение тренда. для выражения равномерного роста (снижения) и криволинейными зависимостями типа гиперболы, параболы, степенной функции для выражения замедленного или ускоренного роста (снижения).
для выражения равномерного роста (снижения) и криволинейными зависимостями типа гиперболы, параболы, степенной функции для выражения замедленного или ускоренного роста (снижения). .
.

 ;
;  ;
;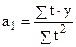 ;
;

 .
. , где
, где  - уровни динамического ряда, вычисленные по соответствующему аналитическому уравнению на момент времени t. Выбор формы кривой во многом определяет результаты экстраполяции тренда. Основанием для выбора вида кривой может использоваться содержательный анализ сущности развития данного явления. Можно опираться также на результаты предыдущих исследований в данной области.
- уровни динамического ряда, вычисленные по соответствующему аналитическому уравнению на момент времени t. Выбор формы кривой во многом определяет результаты экстраполяции тренда. Основанием для выбора вида кривой может использоваться содержательный анализ сущности развития данного явления. Можно опираться также на результаты предыдущих исследований в данной области.


