
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Средняя величина в статистике, ее сущность и условия применения.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Средняя величина является обобщающей характеристикой изучаемой совокупности, показывающей типичный уровень варьирующего признака в расчете на единицу совокупности. Средняя всегда обобщает количественную вариацию признака, т.е. в средних величинах погашаются индивидуальные различия единиц совокупности, обусловленные случайными обстоятельствами. В отличие от средней абсолютная величина, характеризующая уровень признака отдельной единицы совокупности, не позволяет сравнивать значения признака у единиц, относящихся к разным совокупностям. Так, если нужно сопоставить уровни оплаты труда работников на двух предприятиях, то нельзя сравнивать по данному признаку двух работников разных предприятий. Оплата труда выбранных для сравнения работников может быть не типичной для этих предприятий. Если же сравнивать размеры фондов оплаты труда на рассматриваемых предприятиях, то не учитывается численность работающих и, следовательно, нельзя определить, где уровень оплаты труда выше. В конечном итоге сравнить можно лишь средние показатели, т.е. сколько в среднем получает один работник на каждом предприятии. Таким образом, возникает необходимость расчета средней величины как обобщающей характеристики совокупности. 16 Виды (степенные: средняя арифметическая, средняя гармоническая, средняя геометрическая, средняя хронологическая, и структурные: мода, медиана) и формы (простая и взвешенная) средних. Средние величины, используемые в статистике, относятся к двум классам: степенные и структурные средние. Среди степенных средних в статистическом анализе наибольшее применение нашли: 1) Средняя арифметическая простая где Средняя арифметическая простая используется в том случае, если у всех группировочных признаков равны между собой частоты признака. 2) Средняя арифметическая взвешенная – используется, если частоты признака не равны между собой 3) Средняя гармоническая взвешенная используется при отсутствии данных о частотах признака, (F = x·f) и вариантами признака (х) 4) Средняя гармоническая простая используется в том случае, если у всех вариантов признака равны между собой объемы признака (F=const)
5) Средняя квадратическая ( взвешенная 6) Средняя геометрическая ( взвешенная К структурным средним, наиболее часто используемым статистикой, относят Моду и медиану. Мода (Мо) – это значение признака, наиболее часто встречающегося в данном ряду. В дискретном ряду распределения моду определяют по наибольшей частоте. В интервальном ряду распределения мода определяются по формуле
где Модальный интервал выбирается по максимальной частоте в исследуемом ряду распределения. Медиана (Ме) – это значение признака, которое приходится на середину ранжированного ряда распределения. Ранжированный ряд распределения представлен значениями всех признаков в порядке возрастания. Порядковый номер признака в ранжированном ряду распределения определяется по сумме накопленных частот (кумулятивным частотам). В дискретном ряду распределения медиана определяется исходя из условий: Если в вариационном ряду
Если в вариационном ряду
В интервальному ряду распределения медиана определяется по формуле
где Медианный интервал определяется по кумулятивным частотам, где впервые сумма частот превысит половину всех частот. Выбор вида средней для характеристики совокупности производится в зависимости от особенностей изучаемого явления и от цели определения средней. Понятие вариации. Конкретные условия, в которых находится каждый из изучаемых объектов, а также особенности их собственного развития (социальные, экономические и пр.) выражаются соответствующими числовыми уровнями статистических показателей. Таким образом,вариация, т.е. несовпадение уровней одного и того же показателя у разных объектов, имеет объективный характер и помогает познать сущность изучаемого явления. Показатели вариации: размах вариации, среднее линейное отклонение, дисперсия, среднее квадратичное отклонение, коэффициент вариации, коэффициент осцилляции, линейный коэффициент вариации и методика их расчета. Размах вариации (R)= Среднее линейное отклонение (Д) представляет собой среднюю арифметическую из абсолютных значений отклонений вариантов от средней. Рассчитывают: простое взвешенное Дисперсия ( простая взвешенная Преобразовав указанные формулы определения дисперсии, можно получить упрощенный вариант формулы (дисперсия методом моментов)
Среднее квадратическое отклонение ( Достоинство среднего квадратического отклонения по сравнению со средним линейным отклонением в том, что при его вычислении никакого условного допущения о необходимости суммирования отклонений вариантов от средней без учета их знаков не делается. Показатели относительного рассеивания: Коэффициент вариации используют для сравнения рассеивания двух и более признаков, имеющих различные единицы измерения. Коэффициент вариации представляет собой относительную меру рассеивания, выраженную в процентах. Он вычисляется по формуле: где Коэффициентом осцилляции отражает относительную колеблемость крайних значений признака вокруг средней
Линейный коэффицинт вариации - это отношение среднего линейного отклонение к средней арифместической: С помощью линейного коэффицинта вариации можно сравнивать вариацию разных совокупностей, потому что в отличие от среднего линейного отклонения его значение не зависит от единиц измерения X.
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 535; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.123.10 (0.006 с.) |


 – средняя арифметическая; хi – отдельные варианты признака; n – количество групп.
– средняя арифметическая; хi – отдельные варианты признака; n – количество групп.

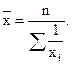
 )простая
)простая 

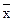 ) простая
) простая 


 - нижняя граница модального интервала;
- нижняя граница модального интервала;  - величина модального интервала;
- величина модального интервала;  - частота модального интервала;
- частота модального интервала;  - частота интервала, предшествующего модальному;
- частота интервала, предшествующего модальному; 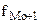 - частота интервала, следующего за модальным.
- частота интервала, следующего за модальным. случаев (нечетное число), то значение признака у случая
случаев (нечетное число), то значение признака у случая  будет медианным, т.е.
будет медианным, т.е. .
.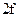 случаев (четное число), то медиана равна средней арифметической из двух серединных значений
случаев (четное число), то медиана равна средней арифметической из двух серединных значений

 - начало медианного интервала;
- начало медианного интервала;  - величина медианного интервала;
- величина медианного интервала;  - сумма накопленных частот до медианного интервала;
- сумма накопленных частот до медианного интервала;  - частота медианного интервала.
- частота медианного интервала. .
. ,
, .
. ) наиболее часто используемый показатель вариации, показывает среднюю площадь отклонений вариантов признака от средней величины.
) наиболее часто используемый показатель вариации, показывает среднюю площадь отклонений вариантов признака от средней величины. ,
, .
.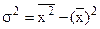 .
.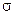 ) определяется как квадратный корень из дисперсии.
) определяется как квадратный корень из дисперсии.  .
.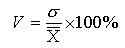 ,
, - искомый показатель,
- искомый показатель,  - среднее квадратичное отклонение,
- среднее квадратичное отклонение, 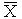 - средняя величина.
- средняя величина. .
. , где Л – среднее линейное отклонение
, где Л – среднее линейное отклонение


