
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Относ.стат. величины, их виды и формы выраженияСодержание книги
Поиск на нашем сайте
Относительная величина – это обобщающий показатель, полученный в результате сравнения двух абсолютных величин. Величина, с которой сравнивают (знаменатель) называется базой сравнения (основание), а сравниваемая величина (числитель) называется текущей (отчетной) пок-тель. Относительные величина в зависимости от базы сравнения могут быть выражены в: a Коэффициентах; a Процентах (если база сравнения равна 100); a Промилях (если база сравнения равна 1000); a Именованных величинах (человек/км2 По своему содержанию относительные величины делятся на виды: 1. относительная величина прогноза (% выполнения плана) 2. Относительная величина структуры 3. Относительная величина динамики 4. Относительная величина сравнения: сравнивается одноименные показатели в различных территорий и объектов (например, добыча угля). 5. Относительная величина интенсивности: здесь сравниваются разноименные показатели в разрезе различных территорий и объектов. Это всегда именованная величина (например, потребление продуктов питания на душу населения); 6. Относительная величина координации (соотношение отдельных частей целого между собой,).
Относительная величина динамики используется для характеристики изменения явления во времени. Вычисляются путем отношения величины текущего периода к величине одного из прошлых периодов. Расчет показателей с постоянной и переменной базой. ОВД= текущей показатель \ предыдущей (или базиный) показатель Базисные-сравнение осущь с одним и тем-же базисным уровнем (первым годом) Цепные –сравнение осуществляется с предыдущем уровнем 19. Сущность статистических средних величин, их виды и правила их применения Средняя величина – это обобщающий показатель, характеризующий однотипные общественные явления по одному количественному признаку в конкретных условиях места и времени. Например, средняя продолжительность жизни. Первым условием применения средних величин является тот факт, что все средние должны опираться на массовые общественные явления. Вторым условием применения средних является тот факт, что групповые средние должны дополняться общими средними (ср. урожайность пшеницы в области и средняя в РФ). Третьим условием является то, что все показатели средних должны определяться по однородной совокупности. Виды: степенные, структурные. Выбор зависит от цели исследования, экон сущности, хар-ра данных
20. Простая и взвешенная средняя арифметичекая Средняя арифметическая простая равна сумме показателей (уровней), деленной на число показателей (уровней). Средняя арифметическая взвешенная принимается в тех случаях, когда известны отдельные значения признака и их веса (fi), т.е. частота повторения признака.
Средняя арифметическая взвешенная равна сумме произведений признака на вес, деленной на сумму веса. Если показатель в виде интервала то необходимо определить середину интервала по средней арифметической простой, а затем производить последующий расчет.
21 Основные свойства средней арифметической. 1. Если из всех вариантов ряда вычесть или ко всем вариантам добавить постоянное число, то средняя арифметическая соответственно уменьшится или увеличится на это число. 2. Если все варианты ряда умножить или разделить на постоянное число, то средняя арифметическая соответственно увеличится или уменьшится в это число раз. 3. Если все частоты увеличить или уменьшить в постоянное число раз, то средняя от этого не изменится. 4. Сумма отклонений всех вариантов ряда от средней арифметической равна 0. (Нулевое свойство средней). 5. Общая средняя совокупности равна средней арифметической из частных средне взвешенных по объемам частных совокупностей. 6. Сумма квадратов отклонений всех вариантов ряда от средней арифметической меньше суммы квадратов их отклонений от любого другого постоянного числа. 7. Средний квадрат отклонений вариантов ряда от произвольного числа А равен дисперсии плюс квадрат разности между средней и этим числом А
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 188; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.99.192 (0.007 с.) |



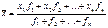
 .
. .
. .
. .
. , где
, где  - средняя арифметическая частных групп,
- средняя арифметическая частных групп,  - численность соответствующих групп,
- численность соответствующих групп,  - общая средняя.
- общая средняя.



