
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление средней из вариационного ряда способом моментоСодержание книги
Поиск на нашем сайте Способ моментов Способ моментов предполагает следующие действия: 1) Если возможно, то уменьшаются веса. 2) Выбирается начало отсчета – условный нуль. Обычно выбирается с таким расчетом, чтобы выбранное значение признака было как можно ближе к середине распределения. Если распределение по своей форме близко к нормальному, но за начало отсчета выбирают признак, обладающий наибольшим весом. 3) Находятся отклонения вариантов от условного нуля. 4) Если эти отклонения содержат общий множитель, то рассчитанные отклонения делятся на этот множитель. 5) Находится среднее значение признака по следующей формуле
23. Средняя гармоническая применяется в тех случаях, когда известно отдельные значения признака X и объемы признаков. Объемом может быть: фонд з/п,стипендиальный фонд. В этой формуле наблюдается обратная связь, т.е. при делении 2-ух показателей получается 3 имеющий экономический смысл. Например, при делении фактического товарооборота на количество проданных товаров мы получим цену товара. Формула средней гармонической простой:
Эта формула обратная средней арифметической простой и предполагается, что сумма объемов в данном случае равна единице. Средняя гармоническая взвешенная:
Средняя гармоническая взвешенная равна сумме объемов признаков деленная на сумму отношения объема к признаку.
24.. Средняя квадратическая:
средн.геометр.: П-произведение
Общая ф-ла:
25 Мода – значение случайной величины, которая встречается с наибольшей вероятностью в дискретном вариационном ряду (Mo). Медиана – это вариант, который расположен в середине вариационного ряда. Медиана делит вариационный ряд на две равные части; т.е. со значением признака меньше медианы и со значением признака больше медианы. мода определяется по формуле:
где
В вариационном ряду с нечетным числом показателей, нахождение медианы определяется по формуле: В интервальном ряду для нахождения значения медианы используется формула линейной интерполяции:
xme – нижняя граница медианного интервала; ime – медианный интервал; - половина от общего числа наблюдений; Sme-1 – сумма наблюдений, накопленная до начала медианного интервала; fme – число наблюдений в медианном интервале. Квартиль, дециль Квартили (четверти) отсекают от совокупности соответственно 25%, 50% и 75%. различают: квартиль нижний (отделяет 1\4), квартиль верхний (отделяет 1\4 часть сов-ти с наиб значением признака), квартиль средний=медиане
Децили отсекают от совокупности соответственно 10%, 20%, 30% и т.д. 1 дециль (делит 1\10 к 9\10) 2 дециль (делит 2\10 к 8\10)-разновидность медианы
27. Вариация представляет собой изменение цифровых значений признака. Размах вариации- разница между максимальным и минимальным значениями признака. Размах вариации служит лишь приближенной мерой вариации признака, Для более полной характеристики степени варьирования признака применяются следующие показатели:
Среднее квадратическое отклонение – показатель вариации, характеризующий величину, на которую в среднем признаки по единица наблюдения отличаются от средней арифметической:
28. Дисперсия – это средняя из квадратов отклонений от средней арифметической:
Коэффициент вариации является относительной мерой степень варьирования признака, который определятся как отношение среднеквадратического отклонения к среднему показателю (в %).
29 Дисперсия – это средняя из квадратов отклонений от средней арифметической:
Св-ва 1. Дисперсия постоянной величины равна нулю. 2. Уменьшение или увеличение каждого значения признака на одну и ту же постоянную величину А дисперсии не изменяет. 3. Уменьшение или увеличение каждого значения признака в какое-то число раз к соответственно уменьшает или увеличивает дисперсию в 4. Дисперсия признака относительно произвольной величины всегда больше дисперсии относительно средней арифметической на квадрат разности между средней и произвольной величиной:
общая дисперсия s2 измеряет вариацию признака всей совокупности под влиянием всех факторов, обуславливающих вариацию. межгрупповая дисперсия характеризует вариацию результативного признака под влиянием одного признака фактора положенного в основу группировки d2=S(xcp i - xcp)2f/Sf внутригрупповая дисперсия, которая отражает случайную вариацию происходящую под влиянием неучтенных факторов. Общая дисперсия равна сумме средней из внутригрупповых и межгрупповых дисперсий:
30. Способ моментов Св-ва 1. Дисперсия постоянной величины равна нулю. 2. Уменьшение или увеличение каждого значения признака на одну и ту же постоянную величину А дисперсии не изменяет. 3. Уменьшение или увеличение каждого значения признака в какое-то число раз к соответственно уменьшает или увеличивает дисперсию в 4. Дисперсия признака относительно произвольной величины всегда больше дисперсии относительно средней арифметической на квадрат разности между средней и произвольной величиной:
На данных св-вах основан способ моментов
А-знач признака облад наиб частотой -условный момент 2-го порядка
31. р - доля единиц, обладающих данным признаком; q - доля единиц, не обладающих данным признаком.
Средняя арифметическая простая равна сумме показателей (уровней), деленной на число показателей (уровней). Средняя арифметическая взвешенная принимается в тех случаях, когда известны отдельные значения признака и их веса (fi), т.е. частота повторения признака.
Средняя арифметическая взвешенная равна сумме произведений признака на вес, деленной на сумму веса. Если показатель в виде интервала то необходимо определить середину интервала по средней арифметической простой, а затем производить последующий расчет. 32. Статистические ряды распределения представляют собой упорядоченное распределение единиц данной совокупности на группы по определенному варьирующему признаку. Ряд распределения характеризует структуру или состав изучаемого явления, а также позволяется рассматривать однородные совокупности и закономерности, распределения границ и признаков явлений. -Если ряд построен по атрибутивным, качественным признакам, то он назначается атрибутивным. (распределение населения по полу, занятости и т.д.) -Ряд распределения построен по количественному признаку называется вариационным. (распределение работников фирмы по стажу работы). Вариационные ряды могут быть построены в порядке возрастания или убывания. Они также имеют следующие характеристики. Варианта (признак) – x; Частота (вес) – f; Частоть Частота или вес показывает, сколько таких признаков (вариант) находится в данной совокупности, т.е. как часто встречается данный признак в совокупности. з/п в размере 300-400 руб. получают 3 человека. Частоть – это показатели относительных величин, т.е. это проценты или доли в совокупности. Вариационные ряды в зависимости от характера вариации (признака) делятся на дискретные и непрерывные. Ряд распределения может быть: - ранжированный ряд (возрастающий или убывающий), -дискретный (варианты имеют значения целых чисел. число членов семьи - 2,3, 4,5 и т.д.) -интервальный (значения вариант даются в виде интервалов. размер зарплаты 100-200, 200-300 и т.д.)
Построение рядов 3. интервальные ряды – это таблица состоящая из 2-х граф(сток) интервалов признака вариация которого изучается и число ед совокупности попадающих в данный интервал или долей этого числа от общей числ-ти сов-ти. 4. дискретные ряды – это таблица состоящая из 2-х граф(или строк): конкретных значений варьирующего признака(вариант) и числа единиц сов-ти с данным значением признака(частот) или долей этого числа от общей чист-ти сов-ти (частностей). Ряды распред-ния графически можно изобразить при помощи полигона, гистограммы и кумуляты. На оси абсцисс отклад-тся зн-ния вариантов, на оси ординат значения частот или частостей. Дискрет.ряд на графике изображается в виде полигона распред-ния в форме кривой. Интервал.ряд грф-ки изобр-тся в виде гистограммы. Гистограмма может быть преобразована в полигон распр-ния, для чего середины верхних сторон прямоугольников соединяются отрезками прямых.
33 Статистическое наблюдение – это планомерный, научно организованный, систематический сбор необходимых данных по явлениям, процессам общественной жизни. Требования: достоверность, полнота, сопоставляемость, своевременность. Любое стат. наблюдение начинается с: 1) Постановления цели и задачи; 2)Выбор Объекта наблюдения (совокупность подлежащая исследованию); 3)Выбор Единицы наблюдения (часть объекта (совокупности) наблюдения); 4)Определение программы наблюдения (перечень вопросов показателей по которым будет производится наблюдение) оформляется в виде бланков с инструкцией, которая разъясняет смысл проведения работы.). Существуют 3 формы стат. наблюдения: 1)Отчётность: сведения предоставляются в виде формуляра регламентированного образца. (она документально и юридически заверена); 2)Специально организованное обследование. -(перепись населения.). 3) регистровое наблюдение Виды стат набл.: 1)Текущее- производится непрерывно (конвейер); 2)Периодическое - (перепись населения); 3)Единовременное- производится в разовом порядке. Способы: непосредственное наблюдение, документальный способ, Опрос.(устный, саморегистрация, корреспондентский. Наблюдение может быть сплошным (генеральная сов-ть) и не сплошны м (выборочная сов-ть), повторным и не повторным.
Программа наблюдения Объект наблюдения – совокупность предметов, явлений, у которых должны быть собраны сведения. Единица наблюдения – это составной элемент объекта, который является носителем признаков, подлежащих регистрации и основой счета. Ценз – это определенные количественные ограничения для объекта наблюдения. Программа наблюдения – это перечень признаков, подлежащих регистрации. Программа находит отражение в формуляре наблюдения. Выделяются организационные вопросы: перечень мероприятий, обеспечивающих правильность наблюдения, а также оргплан, где учитываются органы наблюдения, время наблюдения, порядок приема и сдачи материала, порядок получения информации. требования: - П. должна содержать существенные признаки, непосредственно характеризующие изучаемые явление, его тип, основные черты, свойства; - не следует включать второстепенные вопросы,; - при разработке надо стремиться к полноте собираемых сведений; - лаконичность; - формулировка вопросов точной; следует включить контрольные вопросы. Критический момент – момент времени, по состоянию на который производится регистрация наблюденных фактов.
34. Ошибки наблюдения по источникам и причинам возникновения можно разделить на две группы: -Ошибки регистрации; -Ошибки репрезентативности. Ошибки регистрации связаны с неправильным установлением и/или отражением фактов в процессе наблюдения, могут быть: Случайные ошибки, которые возникают из-за невнимательности или усталости регистратора или респондента; Систематические ошибки регистрации, которые бывают: Преднамеренные ошибки, которые возникают из-за нежелания респондента дать объективную информацию; Непреднамеренные систематические ошибки возникают из-за недостаточной квалификации регистраторов. Ошибки репрезентативности возникают при несплошном наблюдении из-за несоответствия составов генеральной и отобранной совокупностей, бывают: Случайные ошибки, которые характерны для выборочного метода и обусловлены волею случая; Систематические ошибки возникают из-за неправильно проведенного отбора. Случайные ошибки поддаются расчету с помощью специальных методов, систематические не поддаются. Для предотвращения ошибок применяются: Логический контроль – проверка логической совместимости собранных данных; Арифметический контроль – подсчет и проверка итогов по строкам и столбцам, проверка значений расчетных показателей.
Средняя ошибка выборки. Средняя ошибка выборки представляет собой такое расхождение между средними выборочной и генеральной совокупностями ( Она зависит от следующих моментов: 1) при соблюдении принципа случайного отбора средняя ошибка выборки определяется прежде всего объемом выборки: чем больше численность при прочих равных условиях, тем меньше величины средней ошибки выборки. Генеральная совокупность характеризуется тем точнее, чем больше единиц данной совокупности охватывается выборочным наблюдением; 2) степени варьирования признака. Степень варьирования характеризуется дисперсией
36.Предельная ошибка выборки. Если выборка достаточно велика (объем составлял не мене 20 единиц), то считается что ошибка распределена по нормальному закону. Таким образом, зная закон распределения ошибки, можно определить предельную ошибку выборки и тем самым – оценить границы интервала, за которые ошибка выйдет с заданной вероятностью (доверительной вероятностью). Такой интервал называется доверительным. Предельная ошибка определяется по формуле: где
|
||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 309; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.57 (0.013 с.) |

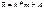
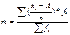
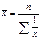
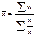 ;
; 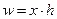

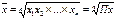
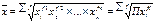
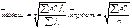
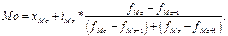
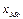 - начальное значение интервала, содержащего моду;
- начальное значение интервала, содержащего моду;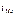 - величина модального интервала;
- величина модального интервала; 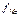 - частота модального интервала;
- частота модального интервала; 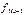 - частота интервала, предшествующего модальному;
- частота интервала, предшествующего модальному; 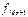 - частота интервала, следующего за модальным.
- частота интервала, следующего за модальным.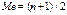
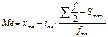 , где
, где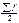
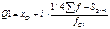
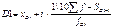
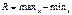
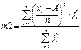 Среднее линейное отклонение – это средняя арифметическая абсолютных отклонений значений признака от среднего уровня:
Среднее линейное отклонение – это средняя арифметическая абсолютных отклонений значений признака от среднего уровня: ;
; 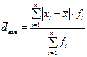 ,
,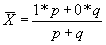
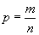
 ;
;  .
. ;
; 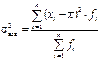 ,
,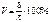
 ;
; 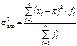 ,
, раз, а среднее квадратическое отклонение - в к раз.
раз, а среднее квадратическое отклонение - в к раз.
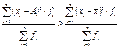
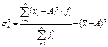
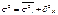
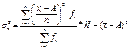 h-ширина интервала
h-ширина интервала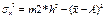
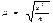

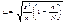 Альтернативным называются признаки, которыми обладают одни единицы совокупности и не обладают другие. Их вариация проявляется в значении "0" у единиц, которые этим признаком не обладают, или "1" у тех, которые данный признак имеют.
Альтернативным называются признаки, которыми обладают одни единицы совокупности и не обладают другие. Их вариация проявляется в значении "0" у единиц, которые этим признаком не обладают, или "1" у тех, которые данный признак имеют.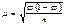 -среднее знач альтернативного признака
-среднее знач альтернативного признака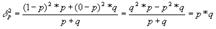
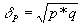 -дисперсия альтернативного признака
-дисперсия альтернативного признака
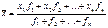
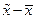 ), которое не превышает ±
), которое не превышает ±  .
.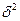 или, для альтернативного признака,w(1-w). Чем меньше вариация признака, а следовательно, и дисперсия, тем меньше средняя ошибка выборки, и наоборот. При нулевой дисперсии (признак не варьирует) средняя ошибка выборки равна нулю, т. е. любая единица генеральной совокупности будет совершенно точно характеризовать всю совокупность по этому признаку.
или, для альтернативного признака,w(1-w). Чем меньше вариация признака, а следовательно, и дисперсия, тем меньше средняя ошибка выборки, и наоборот. При нулевой дисперсии (признак не варьирует) средняя ошибка выборки равна нулю, т. е. любая единица генеральной совокупности будет совершенно точно характеризовать всю совокупность по этому признаку.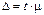
 – предельная ошибка выборки;
– предельная ошибка выборки;  – средняя ошибка выборки;
– средняя ошибка выборки;  – коэффициент доверия.
– коэффициент доверия.


