
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод аналитического выравнивания рядов динамики.Содержание книги
Поиск на нашем сайте
Аналитическое выравнивание ряда динамики используется для того, чтобы дать количественную модель, выражающую основную тенденцию изменения уровней динамического ряда во времени. Он характеризуется тем, что фактические уровни ряда заменяются уровнями, которые вычислены на основе определенной функции, выбранной в предположении, что она наилучшим образом описывает эмпирические данные. На практике исследований применяется аналитическое выравнивание по прямой, гиперболе, параболе разных порядков, экспоненте. Выравнивание по прямой используется в тех случаях, когда абсолютные приросты практически постоянны, т, е. когда уровни изменяются в арифметической прогрессии или близко к ней. А выравнивание по показательной функции применяется в случаях, когда ряд отражает развитие в геометрической прогрессии, т. е. когда цепные коэффициенты роста практически постоянны.
43.Сезонные колебания – это более или менее устойчивые колебания внутри года, кот.вызваны специф.условиями пр-ва или потребления. Знание сезонных колебаний позволяет осуществить рациональное внутригодовое и внутримесячное планирование. Сезонность изм-тся путем исчисления индекса зезонности, для чего надо иметь помесяч.данные, или по квартальные, не менее чем за три года (5 лет):
44.Индексы, их сущность, значение и виды. Индекс - это показатель являющийся относительной величиной сравнения. Он показывает во сколько раз уровень социально-экономического явления отличается от уровня того же явления в у других условиях. индексы используются для сопоставления с уровней изучаемого явления. Определение факторов влияющих на уровень социально-экономического явления. индивидуальный индекс (i) - если все уровня являются одинаковую размерность. общий индекс (I) - мулитификальная модель итогового показателя. -индекс средних величин. В статистике индексами называют относительные показатели, характеризующие соотношение явлений во времени, в пространстве или по сравнению с некоторым эталоном (планируемым, нормативным уровнем и т.п.). Индексы делятся на индивидуальные и общие (сводные). Индивидуальный индекс характеризует изменение отдельных элементов той или иной совокупности. Так, индивидуальный индекс цены рассчитывается по формуле где р 1 – цена товара в текущем периоде; р 0 – цена товара в базисном периоде
Индексы, их сущность. Сводный индекс – это сложный относительный показатель, который характеризует среднее изменение социально-экономического явления, состоящего из непосредственно несоизмеримых элементов. Исходной формой сводного индекса является агрегатная. При расчете агрегатного индекса для разнородной совокупности находят такой общий показатель, в котором можно объединить все ее элементы. Например, цены различных товаров складывать неправомерно, однако с экономической точки зрения вполне допустимо суммировать товарооборот по этим товарам. Если мы сравним товарооборот в текущем периоде с его величиной в базисном периоде, то получим сводный индекс товарооборота: На величину данного индекса оказывают влияние как изменение цен, так и изменение объемов реализации. Чтобы оценить изменение только цен (индексируемой величины), необходимо количество проданных товаров (веса индекса) зафиксировать на каком-либо постоянном уровне. Если в качестве веса используют объемный показатель, его обычно фиксируют на уровне текущего периода. Таким способом получают сводный индекс цен (по методу Пааше): Третьим индексом в данной индексной системе является сводный индекс физического объема реализации: .Весами в данном индексе выступают цены, которые фиксируются на базисном уровне. Между рассчитанными индексами существует следующая взаимосвязь: Ip·Iq = Ipq. 45.Агрегатные индексы производительности труда, себестоимости. Для определения общего изменения уровня себестоимости нескольких видов продукции, выпускаемых предприятием, рассчитывается сводный индекс себестоимости. При этом себестоимость взвешивается по объему производства отдельных видов продукции текущего периода: .Числитель этого индекса отражает затраты на производство текущего периода, а знаменатель – условную величину затрат при сохранении себестоимости на базисном уровне. Разность числителя и знаменателя показывает сумму экономии предприятия от снижения себестоимости: Сводный индекс физического объема продукции, взвешенный по себестоимости, имеет следующий вид: ..Третьим показателем в данной индексной системе является сводный индекс затрат на производство: Все три индекса взаимосвязаны между собой: Еще одна область применения индексного метода – анализ изменений в производительности труда. Индивидуальные индексы производительности труда имеют вид: где t – затраты рабочего времени на единицу продукции. Трудоемкость является обратным показателем, поэтому снижение трудоемкости в текущем периоде по сравнению с базисным свидетельствует о росте производительности труда. Располагая данными о трудоемкости различных видах продукции и объемах их производства, можно рассчитать сводный индекс производительности труда:
Сводный индекс физического объема продукции, взвешенный по трудоемкости, имеет следующий вид: Третьим показателем в данной индексной системе является сводный индекс затрат труда (массы отработанного времени): Все три индекса взаимосвязаны между собой: 46. Еще одна область применения индексного метода – анализ изменений в производительности труда. Индивидуальные индексы производительности труда имеют вид:,
 где t – затраты рабочего времени на ед продукции. где t – затраты рабочего времени на ед продукции.
Трудоемкость является обратным показателем, поэтому снижение трудоемкости в текущем периоде по сравнению с базисным свидетельствует о росте производительности труда.
Разность знаменателя и числителя этого индекса показывает сумму экономии затрат труда за счет роста производительности труда.
Сводный индекс физического объема продукции, взвешенный по себестоимости, имеет следующий вид: Третьим показателем в данной индексной системе является сводный индекс затрат на производство: Все три индекса взаимосвязаны между собой:
|
||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 161; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.159.163 (0.008 с.) |

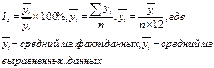
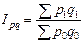 .
.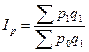 .
.

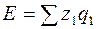


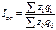
 .
.
 .Разность знаменателя и числителя этого индекса показывает сумму экономии затрат труда за счет роста производительности труда.
.Разность знаменателя и числителя этого индекса показывает сумму экономии затрат труда за счет роста производительности труда. .
.
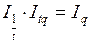

 Располагая данными о трудоемкости различных видах продукции и объемах их производства, можно рассчитать сводный индекс производительности труда:
Располагая данными о трудоемкости различных видах продукции и объемах их производства, можно рассчитать сводный индекс производительности труда:
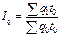 Сводный индекс физического объема продукции, взвешенный по трудоемкости, имеет следующий вид:
Сводный индекс физического объема продукции, взвешенный по трудоемкости, имеет следующий вид: Третьим показателем в данной индексной системе является сводный индекс затрат труда (массы отработанного времени):
Третьим показателем в данной индексной системе является сводный индекс затрат труда (массы отработанного времени):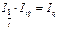 Все три индекса взаимосвязаны между собой:
Все три индекса взаимосвязаны между собой: 47. Для определения общего изменения уровня себестоимости нескольких видов продукции, выпускаемых предприятием, рассчитывается сводный индекс себестоимости. При этом себестоимость взвешивается по объему производства отдельных видов продукции текущего периода:
47. Для определения общего изменения уровня себестоимости нескольких видов продукции, выпускаемых предприятием, рассчитывается сводный индекс себестоимости. При этом себестоимость взвешивается по объему производства отдельных видов продукции текущего периода: Числитель этого индекса отражает затраты на производство текущего периода, а знаменатель – условную величину затрат при сохранении себестоимости на базисном уровне. Разность числителя и знаменателя показывает сумму экономии предприятия от снижения себестоимости:
Числитель этого индекса отражает затраты на производство текущего периода, а знаменатель – условную величину затрат при сохранении себестоимости на базисном уровне. Разность числителя и знаменателя показывает сумму экономии предприятия от снижения себестоимости: 
 .
.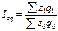
 .
.


