
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: «Расчёт средних величин в статистике».Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Компетенции: Студент следующие навыки и умения: - в определении вида представленных исходных данных (сгруппированы данные или нет, определение группировочного признака, содержания граф таблицы исходных данных); - в области выбора формулы для расчёта среднего значения показателя в зависимости от исходных данных, полученных в результате их обработки, и логического хода рассуждений; - в умении интерпретировать и иллюстрировать графически полученные результаты. Цель работы: Усвоить приемы определения формул для расчёта средних величин и методы их расчёта на основе заданных абсолютных и относительных величин с использованием возможностей приложения Microsoft Excel 7.0. Краткая теория: Средняя величина обобщает качественно однородные значения признака, характеризует объект исследования. В статистике существуют следующие основные виды средних величин: средняя арифметическая; средняя гармоническая; средняя геометрическая; другие виды средних величин (средняя квадратическая, кубическая и т.д.); структурные средние. Выбор формулы для расчёта среднего значения признака начинается с построения исходного соотношения средней (ИСС), которое представляет собой следующую логическую формулу:
Средняя арифметическая используется при известном объёме совокупности и необходимости обобщения самого показателя. Простая средняя арифметическая вычисляется, если известны: индивидуальные значения признака, объем совокупности и совокупность однородна.
Средняя взвешенная используется, если имеются многократные повторения значения признака, совокупность разбита на группы, осредняется группировочный признак: Средняя из групповых средних применяется для расчёта среднего значения результативного признака:
Средняя гармоническая служит для обобщения обратных значений варьирующего признака или при неизвестном объёме совокупности: Например: Имеются данные по фонду заработной платы (ФЗП) в цехах завода и заработная плата (зп) по цехам, тогда средняя заработная плата рабочих завода вычисляется:
Средняя геометрическая величина применяется в том случае, если при замене индивидуальных величин признака на среднюю величину необходимо сохранить неизменным произведение индивидуальных величин: Средняя квадратическая и кубическая величины строятся на основе средней степенной: Структурные средние величины носят название мода и медиана, они описывают структуру совокупности, с ними познакомимся при выполнении следующей лабораторной работы. Пример решения и оформления типовой задачи: Таблица 4.1
Рассчитать среднюю цену 1 кг реализованного риса в коммерческих магазинах фирмы, если: а) известны данные в графах 1 и 2; б) известны данные в графах 1 и 3; в) известны данные в графах 2 и 3; Какие формулы средних величин использовались в п.1,2,3 и почему? а) Значения во всех расчётах одинаковы, но следует обратить внимание на единицы измерения исходных данных. Таблица 4.2 Данные о величине вкладов в коммерческом банке
1. Рассчитать средний размер вклада в банке. Какая формула использована и почему? 2. Опишите структуру вкладчиков по размеру вклада. Какая формула использована и почему? Таблица 4.3
Рис.4.1. Структура вкладчиков коммерческого банка по величине вклада. Контрольные вопросы: 1. Назовите виды средних величин в статистике, формулы для вычисления средних величин и приемы для выбора формулы для вычислений. 2. Какие из формул для расчёта средней величины применяли в лабораторной работе и почему? 3. Приведите примеры расчёта простой средней арифметической простой и взвешенной. 4. Приведите примеры расчёта средней величины с помощью средней гармонической. 5. Сделайте выводы по результатам выполненной работы.
Лабораторная работа № 5 Тема: «Структурные средние величины». Компетенции: Студент получает возможность приобрести компетентность: - в подготовительных мероприятиях (поиске модального и медианного интервалов) перед расчётами; - в оценке структуры совокупности с помощью расчёта специальных характеристик в случае представления исходных данных в виде интервального ряда; - в проведении оценки правильности расчётов соответствующих величин; - в понимании значения структурных средних и экономической интерпретации полученных результатов при расчёте моды и медианы ряда данных, характеризующих различные процессы и явления. Цель работы: Приобрести навык в расчётах структурных средних величин в статистике с использованием возможностей приложения Microsoft Excel 7.0 и выполнении оценок на основе полученных значений структурных средних. Краткая теория: Вариационные или количественные ряды в статистике делятся на ряды со сгруппированными и не сгруппированными данными. В зависимости от вида ряда расчёт моды и медианы для этих рядов различно. Определение 1: Модой в статистике (М0) называют величину признака (варианты), которая чаще всего встречается в совокупности. Примечание: Для вариационного ряда по не сгруппированным данным моды не существует. Определение 2: Медианой в статистике (Ме) называется варианта, которая находится в середине ряда (центральная варианта). Определение 3: Кумулятивная частота i-й группы получается суммированием кумулятивной частоты (i-1)-й группы и частоты i-й группы, т.е. кумулятивная частота текущей группы получается суммированием кумулятивной частоты предшествующей группы и частоты текущей. Ме вариационного ряда по несгруппированным данным равна: - центральной варианте для рядов с нечётным числом единиц совокупности; - полусумме центральных для рядов чётным числом единиц совокупности. Мода и медиана дискретного ряда Мода дискретного ряда равна варианте с наибольшей частотой (весом), медиана соответствует варианте, для которой кумулятивная частота³ Мода и медиана интервального ряда Определение 4: Модальным интервалом называется интервал с наибольшей частотой. Определение 5: Медианным интервалом называется интервал, где кумулятивная частота³ Формулы для расчёта моды и медианы интервального ряда:
Пример решения и оформления типовой задачи: Имеются данные по продаже акций на бирже, рассчитать структурные средние величины ряда, описать структуру совокупности, выполнить графическое изображение вариационного ряда: Таблица 5.1.
Продолжение таблицы 5.1
Подготовительные расчёты разместим в таблице 5.2, из построений нетрудно увидеть, что модальный интервал [14,5;15,5], медианный интервал (212/2=106) [15,5;16,5]. Таблица 5.2
Тогда
Рис.6.1 Графическое изображение ряда распределения продаж ценных бумаг Контрольные вопросы: 1. Дайте понятие рядов с несгруппированными данными. 2. Какие ряды в статистике называют ранжированными рядами? 3. Какие ряды в статистике называют дискретными рядами? Приведите пример. 4. Какие ряды в статистике называют интервальными рядами? Приведите пример. 5. Что называют модой в статистике? Что называют медианой в статистике? 6. Чему равна мода и медиана рядов с несгруппированными данными? 7. Что называется кумулятивной частотой? 8. Чему равна мода и медиана дискретного ряда? 9. Дайте понятие модального и медианного интервалов. Чему равна мода и медиана интервального ряда? 10. Сделайте выводы по результатам выполненной работы. Лабораторная работа № 6.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1291; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.181.90 (0.008 с.) |

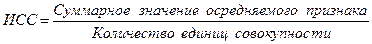

 где
где  индивидуальное значение i- ого признака, n - объем совокупности.
индивидуальное значение i- ого признака, n - объем совокупности. , где
, где  где
где  среднее значение признака в i -ой группе, к - число групп.
среднее значение признака в i -ой группе, к - число групп. , где Mi – объём изучаемого явления.
, где Mi – объём изучаемого явления.
 . По этой формуле в статистике рассчитываются средние коэффициенты и темпы роста.
. По этой формуле в статистике рассчитываются средние коэффициенты и темпы роста. . При соответствующих значениях n получаем среднюю квадратическую и кубическую величины. В статистике используются, например, при расчёте мер вариации, с которыми познакомимся позднее.
. При соответствующих значениях n получаем среднюю квадратическую и кубическую величины. В статистике используются, например, при расчёте мер вариации, с которыми познакомимся позднее.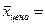 9,3161 рублей; б)
9,3161 рублей; б)  5277,95 руб.
5277,95 руб.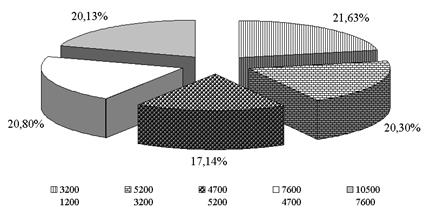

 , где
, где  -частота модального интервала,
-частота модального интервала,  -частота интервала, предшествующего модальному,
-частота интервала, предшествующего модальному,  -частота интервала, следующего за модальным,
-частота интервала, следующего за модальным,  -длина модального интервала,
-длина модального интервала,  -начало модального интервала.
-начало модального интервала. , где SMe-1 - кумулятивная частота интервала, предшествующего медианному,
, где SMe-1 - кумулятивная частота интервала, предшествующего медианному,  - начало медианного интервала,
- начало медианного интервала,  - частота медианного интервала,
- частота медианного интервала,  - длина медианного интервала
- длина медианного интервала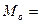 14,9864864,
14,9864864,  16,0238095. На основе расчётов можно сделать следующие выводы: большинство объёмов продаж акций на бирже близки к 16023 рублям, половина продаж составляет объём 14986 рублей.
16,0238095. На основе расчётов можно сделать следующие выводы: большинство объёмов продаж акций на бирже близки к 16023 рублям, половина продаж составляет объём 14986 рублей.



