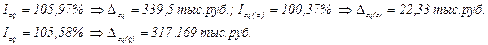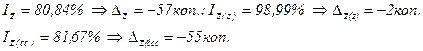Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: «Выполнение арифметического и логического контроля данных статистического наблюдения»Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Астафурова Ирина Сергеевна
Статистика. Лабораторный практикум Учебное пособие Владивосток ББК 65.05 Лабораторный практикум по дисциплине «Статистика» соответствует Государственному образовательному стандарту и структуре курса для экономических специальностей. Целью курса дисциплины приобретение компетентности в области изучения социально-экономических явлений и процессов методами статистики, в решении прикладных задач, отражающих состояние и развитие массовых социально-экономических явлений, с применением компьютерных технологий, интерпретации полученных результатов. Настоящая методическая разработка содержит лабораторный практикум по курсу «Статистика», предназначена для студентов всех форм обучения экономических специальностей, кроме специальности «статистика». Автор: к.э.н., доцент кафедры Бухгалтерского учета и аудита Астафурова И.С. Рецензенты: к.э.н., доцент кафедры Бухгалтерского учёта и аудита Ослопова М.В.; к.э.н., доцент кафедры Бухгалтерского учета и аудита Юдина А.В.
Содержание Страницы Введение 4 Лабораторная работа № 1 5 Лабораторная работа № 2 8 Лабораторная работа № 3 13 Лабораторная работа № 4 18 Лабораторная работа № 5 23 Лабораторная работа № 6 26 Лабораторная работа № 7 33 Лабораторная работа № 8 35 Лабораторная работа № 9 41 Лабораторная работа № 10 49 Лабораторная работа № 11 54 Лабораторная работа № 12 59 Лабораторная работа № 13 67 Лабораторная работа № 14 72 Лабораторная работа № 15 74 Приложения 78 Введение Решение задач в области сбора, научной обработки, обобщения и анализа информации, характеризующей массовые социально-экономические явления и процессы, требует от специалиста определённых знаний и умений. Такие знания и умения даёт общеэкономическая дисциплина «Статистика», которая изучает процессы и явления, происходящие в экономике и обществе на разных уровнях: от государства в целом до отдельного человека. Успешное выполнение этих задач требует дальнейшего улучшения качества подготовки специалистов высокой компетентности и квалификации. Использование современных компьютерных технологий и стандартных пакетов программ при проведении анализа показателей, характеризующих различные экономические явления, предъявляет новые требования к специалистам высокой квалификации, предполагает знание этих технологий и программ и, как следствие, предполагает обучение студентов применению этих технологий в решении различных экономических и социальных задач.
Статистика, как отрасль знаний использует для изучения явлений и процессов различные статистические методы и приёмы (сводка и группировка, расчёт средних, относительных показателей, использование приемов корреляционно-регрессионного анализа, рядов динамики, применение индексного метода и т.д.), которые должна быть применены в прикладной своей части в решении задач лабораторного практикума. Выполнение данного лабораторного практикума базируется на знании и умении применять приложение Microsoft Excel. Приёмы и методы обработки исходных данных используют различные инструментарии таблиц Excel (применение формул при расчётах различных обобщающих абсолютных и относительных показателей, в том числе и индексов, построение графических изображений для иллюстрации выполненных расчётов, оформление выводов по результатам обработки). Особой ценностью обладают выводы, сделанные по результатам работы, которые студенты выполняют самостоятельно на основе произведенных расчётов. Для получения итоговой оценки за экзамен по дисциплине «Статистика» предлагается выполнение студентами следующих видов работ: ·Выполнение практических расчётов в соответствии с данными Методическими указаниями и примерами оформления и решения задачи своего варианта (для всех форм обучения); ·Ответы на контрольные вопросы по выполненной практической части, содержащие вопросы использованного теоретического материала и выводы по результатам расчётов; ·Выполнение ответов на вопросы промежуточной аттестации (для студентов дневной формы обучения) и итоговой для студентов всех форм обучения. Данный лабораторный практикум может быть использован в преподавании дисциплины «Статистика» как для студентов экономических специальностей («Бухгалтерский учёт и аудит», «Маркетинг», «Менеджмент организации», «Математические методы в экономике», «Мировая экономика», «Коммерция», «Финансы и кредит», «Налоги и налогообложение» и т.д., кроме специальности «Статистика»). С учётом особенностей в преподавании дисциплины для разных специальностей следует осуществить выбор выполняемых студентами работ.
Задания для выполнения лабораторного практикума преподаватель может разработать сам, учитывая специальные требования, или использовать электронный вариант заданий автора, представленный в Интегрированной обучающей среде, так как задания должны иметь индивидуальные исходные данные. Каждая лабораторная работа имеет следующую структуру: ÞКомпетенции (перечень приобретаемых знаний и умений); ÞЦель работы (выделяет важные моменты решения задачи); ÞКраткая теория (изложение теоретического материала в части, используемой для решения задачи); ÞПример решения и оформления задачи (содержит основные этапы решения задачи: ход решения, иллюстрация расчётов) без выводов; ÞКонтрольные вопросы, ответы на которые студент готовит для защиты выполненной практической части. В краткой теории излагается лекционный материал, необходимый для выполнения работы; пример решения и оформления задачи описывает алгоритм выполнения расчётов аналогичной задачи, причём пример не содержит выводов, так как эта часть работы выполняется студентом самостоятельно и сообщается преподавателю при ответе на контрольные вопросы; контрольные вопросы содержат вопросы по данной теме из учебного материала и по результатам выполнения работы. Лабораторная работа № 1 Лабораторная работа № 2 Какая группировка построена в Вашей работе, опишите последовательность построения группировки, укажите изучаемую совокупность, единицу совокупности, группировочный признак. Лабораторная работа № 3 Рисунок 3.1. Структура счетов АКБ «Далькомбанк» на 1 января 2008-09 г.г. Для построения графической иллюстрации используется гистограмма, нормированная на 100%, обязательным является правильность построения расчётной таблицы, указания диапазона для графика, всех необходимых атрибутов таблицы. По формулам статистики рассчитаем ОПД по каждому виду вклада, данные заносим в таблицу 3.3. Таблица 3.3 Динамика счетов коммерческого банка «Далькомбанк» 2008-09 г.г.
Рисунок 3.2 Динамика счетов клиентов банка «Далькомбанк» за 2008-09 г.г. Расчёты для последней таблицы следует выполнить после установления самой маленькой величины счёта для каждого показателя времени в таблице исходных данных. Таблица 3.4 Соотношение счетов коммерческого банка «Далькомбанк» 2008-09 г.г.
Рационально использование графика в виде полосовой или линейчатой диаграммы, хотя возможны и другие варианты, всё зависит от личного восприятия исследователя, единственным условием является грамотный выбор диаграммы.
Контрольные вопросы:
1. Что называют абсолютными показателями в статистике? Приведите пример 2. Какими бывают абсолютные величины в статистике в зависимости от единиц измерения? 3. Назовите виды относительных показателей. Приведите пример. Охарактеризуйте каждый относительный показатель 4. Назовите логическую формулу для вычисления каждого относительного показателя. Приведите примеры. 5. Назовите виды графического изображения данных в статистике. 6. Какие виды графиков использовали в лабораторной работе и почему? 7. Сделайте выводы по результатам выполненной работы. Лабораторная работа № 4 Лабораторная работа № 5 Тема: «Структурные средние величины». Компетенции: Студент получает возможность приобрести компетентность: - в подготовительных мероприятиях (поиске модального и медианного интервалов) перед расчётами; - в оценке структуры совокупности с помощью расчёта специальных характеристик в случае представления исходных данных в виде интервального ряда; - в проведении оценки правильности расчётов соответствующих величин; - в понимании значения структурных средних и экономической интерпретации полученных результатов при расчёте моды и медианы ряда данных, характеризующих различные процессы и явления. Цель работы: Приобрести навык в расчётах структурных средних величин в статистике с использованием возможностей приложения Microsoft Excel 7.0 и выполнении оценок на основе полученных значений структурных средних. Краткая теория: Вариационные или количественные ряды в статистике делятся на ряды со сгруппированными и не сгруппированными данными. В зависимости от вида ряда расчёт моды и медианы для этих рядов различно. Определение 1: Модой в статистике (М0) называют величину признака (варианты), которая чаще всего встречается в совокупности. Примечание: Для вариационного ряда по не сгруппированным данным моды не существует. Определение 2: Медианой в статистике (Ме) называется варианта, которая находится в середине ряда (центральная варианта). Определение 3: Кумулятивная частота i-й группы получается суммированием кумулятивной частоты (i-1)-й группы и частоты i-й группы, т.е. кумулятивная частота текущей группы получается суммированием кумулятивной частоты предшествующей группы и частоты текущей. Ме вариационного ряда по несгруппированным данным равна: - центральной варианте для рядов с нечётным числом единиц совокупности; - полусумме центральных для рядов чётным числом единиц совокупности.
Мода и медиана дискретного ряда Мода дискретного ряда равна варианте с наибольшей частотой (весом), медиана соответствует варианте, для которой кумулятивная частота³ Мода и медиана интервального ряда Определение 4: Модальным интервалом называется интервал с наибольшей частотой. Определение 5: Медианным интервалом называется интервал, где кумулятивная частота³ Формулы для расчёта моды и медианы интервального ряда:
Пример решения и оформления типовой задачи: Имеются данные по продаже акций на бирже, рассчитать структурные средние величины ряда, описать структуру совокупности, выполнить графическое изображение вариационного ряда: Таблица 5.1.
Продолжение таблицы 5.1
Подготовительные расчёты разместим в таблице 5.2, из построений нетрудно увидеть, что модальный интервал [14,5;15,5], медианный интервал (212/2=106) [15,5;16,5]. Таблица 5.2
Тогда
Рис.6.1 Графическое изображение ряда распределения продаж ценных бумаг Контрольные вопросы: 1. Дайте понятие рядов с несгруппированными данными. 2. Какие ряды в статистике называют ранжированными рядами? 3. Какие ряды в статистике называют дискретными рядами? Приведите пример. 4. Какие ряды в статистике называют интервальными рядами? Приведите пример. 5. Что называют модой в статистике? Что называют медианой в статистике? 6. Чему равна мода и медиана рядов с несгруппированными данными? 7. Что называется кумулятивной частотой? 8. Чему равна мода и медиана дискретного ряда? 9. Дайте понятие модального и медианного интервалов. Чему равна мода и медиана интервального ряда? 10. Сделайте выводы по результатам выполненной работы. Лабораторная работа № 6. Лабораторная работа № 7. Лабораторная работа № 8. Для изучения корреляционных связей используют уравнение регрессии, которое представляет собой математическое выражение связи признаков: условной средней величины результативного признака с изменением факторного признака (факторный признак- признак, оказывающий влияние на другие признаки, результативный признак- признак, испытывающий на себе влияние факторного).
Уравнение регрессии, выраженное функцией (линейной или нелинейной) и описывающее зависимость условной средней результативного признака от одного факторного - уравнение парной регрессии, а описывающее зависимость результативного от нескольких факторных признаков - уравнение множественной регрессии, т.е. регрессионная модель основана на аналитическом представлении связи факторного и результативного признаков. Простейшим уравнением парной корреляции (регрессии) является линейное уравнение: Для вычисления параметров a и b решается система уравнений:
Можно применять для расчёта параметров уравнения методы линейной алгебры (метод Крамера или метод Гаусса), опуская преобразования, получаем формулу для расчёта:
При линейной корреляционной связи применяют показатель тесноты связи между изучаемыми признаками - коэффициент корреляции:
Коэффициент детерминации (
Таблица характера связи в зависимости от коэффициента корреляции: Таблица 8.1.
Пример решения и оформления типовой задачи: Имеются данные по предприятию о возрасте (продолжительности эксплуатации) типового оборудования и затратах на его ремонт. Рассчитать параметры линейного уравнения парной корреляции, коэффициенты тесноты связи, наименьший возраст оборудования, при котором исчисляются амортизационные отчисления. Сделать выводы по результатам работы. Таблица 8.2.
Рисунок 8.2 Зависимость затрат на ремонт от возраста оборудования На основе графического изображения можно предположить, что аналитическая зависимость между признаками, характеризующими оборудование, существует в виде линейной функции. На основе расчётов, выполненных в таблице 8.3 уравнение линейной парной корреляции имеет вид: Оценка полученного уравнения может быть выполнена несколькими способами, так для линейного уравнения регрессии существует два основных приёма: либо проверка равенства эмпирического коэффициента детерминации и линейного коэффициента корреляции, либо расчёт показателей Контрольные вопросы: 1. Какие виды связей между признаками в статистике знаете? 2. Какие виды уравнений регрессии знаете? 3. Что называется корреляционной связью? 4. Дайте понятие жестко детерминированной связи в статистике. 5. Дайте понятие стохастически детерминированной связи в статистике. 6. Какой признак в статистике является факторным? 7. Какой признак в статистике является результативным? 8. Какой признак в лабораторной работе факторный, а какой результативный? 9. Запишите систему уравнений для определения параметров уравнения парной линейной корреляции. 10. Какие формулы использовали для расчёта коэффициентов в уравнении регрессии в лабораторной работе? 11. Можно ли строить уравнение парной корреляции для сгруппированных данных? 12. Что показывает коэффициент корреляции? 13. Что показывает коэффициент детерминации? 14. Каков экономический смысл параметров в уравнении линейной парной корреляции? 15. Сделайте выводы по лабораторной работе. Таблица 8.3.
Лабораторная работа № 9 Темп прироста
Абсолютное значение 1 % прироста имеет смысл только для цепных характеристик динамических рядов:
Средние величины в рядах динамики: Средний абсолютный прирост
показывает абсолютное изменение показателя в среднем; Лабораторная работа № 10 Тема: «Расчёт экономических индексов в статистике». Компетенции: Студенты при выполнении данной лабораторной работы приобретают компетенции: - в области исследования конкретных процессов происходящих на хозяйствующих субъектах (производства или реализации); - в оценке изменений результирующих показателей, изменяющихся под влиянием соответствующих факторов в абсолютных и относительных величинах, для отдельного хозяйствующего субъекта; - в оценке изменений у разных хозяйствующих субъектов среднего значения качественного показателя в абсолютных и относительных величинах; - в построении уравнения аналитической зависимости показателя, характеризующего изменение явления во времени, и его использование для прогнозирования развития явления в будущем; - в проведении анализа на основе полученных результатов и выполнении выводов. Цель работы: Приобрести навык расчётов экономических индексов как агрегатных, так и средних из индивидуальных с использованием инструментария Microsoft Excel и проведения анализа на основе полученных результатов деятельности предприятия (продажи и производства). Краткая теория: Определение: В статистике под индексом понимают относительный показатель, который выражает соотношение величин какого-либо явления во времени, пространстве, сравнивает фактические данные с любым эталоном (нормативом, планом, прогнозом и т.д.) Основным элементом индексного соотношения является индексируемая величина. Основные обозначения и символы: p - цена (стоимость) единицы товара (продукции); q - количество (объём) какого-либо продукта (товара) в натуральном выражении; z - себестоимость единицы продукции; t - затраты времени на выработку единицы продукции; pq - стоимость продукции (товарооборот); zq - затраты (издержки) на производство продукции; tq - затраты времени (трудоёмкость) на производство продукции и т.д. индивидуальный индекс физического объёма- индивидуальный индекс цены - индивидуальный индекс себестоимости - индивидуальный индекс стоимости (товарооборота) - индивидуальный индекс издержек (затрат)- и т.д., где Определение: Общий индекс в статистике- относительный показатель, служащий для сравнения сложных явлений и включающий в себя индексируемую величину, состояния которой сравниваются и вес- показатель, определяющий значимость каждой индексируемой величины. Общие индексы строятся для количественных и качественных показателей. Кроме этого по способу расчёта показатели делятся на агрегатные индексы и средние из индивидуальных. Определение: Агрегатным индексом называется индекс, у которого числитель и знаменатель представляют собой набор непосредственно несоизмеримых и неподдающихся непосредственному суммированию элементов: сумму произведений двух величин, одна из которых меняется (индексируется), а другая (вес индекса)- остаётся неизменной в числителе и знаменателе, служит для соизмерения индексируемых величин. Типичным индексом количественного показателя является индекс физического объёма. Для вычисления этого индекса, являющегося сложным индексом, введём коэффициенты соизмерения, полученные умножением объёма каждого вида продукции (q) на соответствующую цену (p)- pq; себестоимость(z)- zq; затраты времени(t)- tq и т д. Тогда общий индекс физического объёма продукции (товара):
показывает, как изменилась стоимость в результате изменения объёма выпуска продукции (продаж);
показывает, как изменились издержки производства в результате изменения объёма выпуска продукции (продаж) и т.д. Общий индекс стоимости продукции (общий индекс товарооборота):
показывает, как изменилась стоимость продукции (товарооборот) в текущем периоде по сравнению с базисным. Для расчёта общего индекса как среднего из индивидуальных воспользуемся формулой (1), из которой получим значения недостающих элементов. Так, например, если по имеющейся информации нет значения
и т.д. Общие индексы средних величин. Изучение совместного действия факторов на изменение значения осредняемого признака и изменение структуры явления решается построением системы взаимосвязанных индексов: 1. Индекс переменного состава 2. Индекс постоянного состава 3. Индекс структурных сдвигов Пример решения и оформления задач: Задача 1 Данные о товарообороте в оптовых магазинах коммерческой фирмы. Таблица10.1
1. Произвести оценку выручки магазина № 1 всего и за счёт факторов в абсолютных и относительных величинах; 2. Произвести оценку средней цены на молоко всего и за счёт факторов в относительных и абсолютных величинах; 3. Сделать выводы по каждому пункту, сопровождая их рассчитанными показателями.
Решение: Таблица10.2
1. 2. Задача 2 Данные о затратах на производство сельскохозяйственной продукции Таблица 10.3
В хозяйстве № 1 себестоимость сои уменьшилась на 2%, картофеля увеличилась на 3% и молока увеличилась на 1,2%, в хозяйстве № 2 себестоимость сои осталась без изменения. 1. Произвести оценку изменения затрат в хозяйстве № 1 всего и с разложением по факторам в относительных и абсолютных величинах; 2. Произвести оценку изменения средней себестоимости на одноименную продукцию всего и с разложением по факторам в относительных и абсолютных величинах. Примечание: графу «Объем произведенной продукции» использовать для расчётов в п.2. Решение: 1. Таблица 10.4
Для расчётов в п.1 общего индекса себестоимости используется средний гармонический из индивидуальных, так как значений себестоимости единицы продукции в исходных данных нет.
2. Таблица 10.5
Контрольные вопросы: 1. Назовите индивидуальные индексы и формулы их расчёта, каков экономический смысл индивидуальных индексов? 2. Какие виды общих индексов знаете по способу расчёта? 3. Какие индексы называют общими индексами количественных показателей? 4. Какие индексы называют общими индексами качественных показателей? 5. Какая взаимосвязь существует между количественными и качественными индексами? 6. Каков экономический смысл общего индекса цены (себестоимости, трудозатрат, товарооборота, издержек производства, физического объёма)? 7. Каков экономический смысл разности между числителем и знаменателем общего индекса физического объёма (цены, себестоимости, стоимости реализованной продукции, издержек производства, трудозатрат)? 8. Назовите формулы для расчёта общего индекса стоимости проданной продукции (цены, объёма продаж, затрат на производство продукции, себестоимости) как агрегатного индекса. 9. Назовите формулы для расчёта общего индекса стоимости проданной продукции (цены, объёма продаж, затрат на производство продукции, себестоимости) как среднего арифметического из индивидуальных индексов. 10. Назовите формулы для расчёта общего индекса стоимости проданной продукции (цены, объёма продаж, затрат на пр
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 484; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.96.41 (0.014 с.) |

 Депозитный 1 год
Депозитный 1 год


 , где
, где  -частота модального интервала,
-частота модального интервала,  -частота интервала, предшествующего модальному,
-частота интервала, предшествующего модальному,  -частота интервала, следующего за модальным,
-частота интервала, следующего за модальным,  -длина модального интервала,
-длина модального интервала,  -начало модального интервала.
-начало модального интервала. , где SMe-1 - кумулятивная частота интервала, предшествующего медианному,
, где SMe-1 - кумулятивная частота интервала, предшествующего медианному,  - начало медианного интервала,
- начало медианного интервала,  - частота медианного интервала,
- частота медианного интервала,  - длина медианного интервала
- длина медианного интервала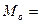 14,9864864,
14,9864864,  16,0238095. На основе расчётов можно сделать следующие выводы: большинство объёмов продаж акций на бирже близки к 16023 рублям, половина продаж составляет объём 14986 рублей.
16,0238095. На основе расчётов можно сделать следующие выводы: большинство объёмов продаж акций на бирже близки к 16023 рублям, половина продаж составляет объём 14986 рублей.
 - среднее значение результативного признака, b - вариация результативного признака на единицу факторного, a - теоретическое значение результативного признака при значении факторного, равное 0 (x=0), что на практике не имеет никакого экономического смысла.
- среднее значение результативного признака, b - вариация результативного признака на единицу факторного, a - теоретическое значение результативного признака при значении факторного, равное 0 (x=0), что на практике не имеет никакого экономического смысла. (8.1)
(8.1)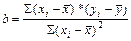 , тогда
, тогда  (8.2)
(8.2) (8.3)
(8.3) ) показывает, какая часть результативного признака обусловлена изменениями факторного:
) показывает, какая часть результативного признака обусловлена изменениями факторного: . Величина коэффициента корреляции колеблется в пределах:
. Величина коэффициента корреляции колеблется в пределах:  .
.
 10
10
 .
. и
и  , сравнение их с табличным значением
, сравнение их с табличным значением 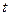 . Из вычислений следует, что минимальное значение факторного признака, при котором возможны изменения результативного равно 29 дней, а 65,699 % изменений затрат обусловлено изменениями возраста оборудования, 34,301 % изменений затрат обусловлено неучтёнными факторами, равенство коэффициента корреляции значению 0,811 говорит об очень сильной связи между изучаемыми признаками.
. Из вычислений следует, что минимальное значение факторного признака, при котором возможны изменения результативного равно 29 дней, а 65,699 % изменений затрат обусловлено изменениями возраста оборудования, 34,301 % изменений затрат обусловлено неучтёнными факторами, равенство коэффициента корреляции значению 0,811 говорит об очень сильной связи между изучаемыми признаками.
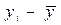


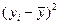


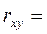

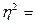
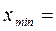
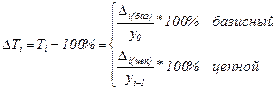 (9.3)
(9.3)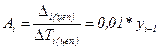 (9.4)
(9.4)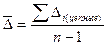 - (9.5)
- (9.5) ; (10.1)
; (10.1)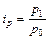 ; (10.2)
; (10.2)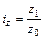 ; (10.3)
; (10.3)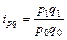 (10.4)
(10.4) (10.5)
(10.5)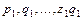 - значения соответствующего показателя в отчётном (текущем) периоде,
- значения соответствующего показателя в отчётном (текущем) периоде, 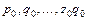 - значения этих показателей в базисном периоде.
- значения этих показателей в базисном периоде.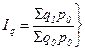 (10.6)
(10.6)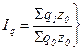 (10.7)
(10.7)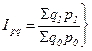 (10.8)
(10.8)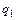 , а имеются значения
, а имеются значения 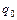 и
и 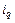 , то
, то 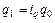 , и тогда:
, и тогда: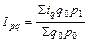 (10.9)
(10.9) ; (10.10)
; (10.10) ; (10.11)
; (10.11)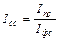 (10.12)
(10.12)