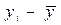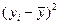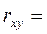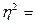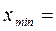Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: «построение линейной парной корреляции»Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Компетенции: Студенты приобретают компетенции: - в области выявления зависимого и независимого признака, поиска аналитического выражения зависимости признаков, характеризующих реальные социально-экономические процессы; - в выборе уравнения регрессии для эмпирических данных и его оценке (адекватность построенной модели); - в оценке связи по различным позициям: наличие связи, её направление, сила и теснота; - в проведении анализа на основе полученных результатов и выполнении выводов. Цель работы: Приобрести навык в построении линейного уравнения регрессии для эмпирических данных, в нахождении параметров уравнения на основе этих данных; в расчёте коэффициента тесноты связи изучаемых признаков с использованием инструментария Microsoft Excel и проведение анализа на основе полученных результатов. Краткая теория:
Рис. 8.1 Типы связей между статистическими признаками Так корреляционная связь является частным случаем статистической. Определение: Корреляционной связью называется такая связь между явлениями и их признаками, когда разным значениям переменной соответствуют различные средние значения другой переменной, причём одному среднему значению может соответствовать множество значений другой переменной. Для изучения корреляционных связей используют уравнение регрессии, которое представляет собой математическое выражение связи признаков: условной средней величины результативного признака с изменением факторного признака (факторный признак- признак, оказывающий влияние на другие признаки, результативный признак- признак, испытывающий на себе влияние факторного). Уравнение регрессии, выраженное функцией (линейной или нелинейной) и описывающее зависимость условной средней результативного признака от одного факторного - уравнение парной регрессии, а описывающее зависимость результативного от нескольких факторных признаков - уравнение множественной регрессии, т.е. регрессионная модель основана на аналитическом представлении связи факторного и результативного признаков.
Простейшим уравнением парной корреляции (регрессии) является линейное уравнение: Для вычисления параметров a и b решается система уравнений:
Можно применять для расчёта параметров уравнения методы линейной алгебры (метод Крамера или метод Гаусса), опуская преобразования, получаем формулу для расчёта:
При линейной корреляционной связи применяют показатель тесноты связи между изучаемыми признаками - коэффициент корреляции:
Коэффициент детерминации (
Таблица характера связи в зависимости от коэффициента корреляции: Таблица 8.1.
Пример решения и оформления типовой задачи: Имеются данные по предприятию о возрасте (продолжительности эксплуатации) типового оборудования и затратах на его ремонт. Рассчитать параметры линейного уравнения парной корреляции, коэффициенты тесноты связи, наименьший возраст оборудования, при котором исчисляются амортизационные отчисления. Сделать выводы по результатам работы. Таблица 8.2.
Рисунок 8.2 Зависимость затрат на ремонт от возраста оборудования На основе графического изображения можно предположить, что аналитическая зависимость между признаками, характеризующими оборудование, существует в виде линейной функции. На основе расчётов, выполненных в таблице 8.3 уравнение линейной парной корреляции имеет вид: Оценка полученного уравнения может быть выполнена несколькими способами, так для линейного уравнения регрессии существует два основных приёма: либо проверка равенства эмпирического коэффициента детерминации и линейного коэффициента корреляции, либо расчёт показателей
Контрольные вопросы: 1. Какие виды связей между признаками в статистике знаете? 2. Какие виды уравнений регрессии знаете? 3. Что называется корреляционной связью? 4. Дайте понятие жестко детерминированной связи в статистике. 5. Дайте понятие стохастически детерминированной связи в статистике. 6. Какой признак в статистике является факторным? 7. Какой признак в статистике является результативным? 8. Какой признак в лабораторной работе факторный, а какой результативный? 9. Запишите систему уравнений для определения параметров уравнения парной линейной корреляции. 10. Какие формулы использовали для расчёта коэффициентов в уравнении регрессии в лабораторной работе? 11. Можно ли строить уравнение парной корреляции для сгруппированных данных? 12. Что показывает коэффициент корреляции? 13. Что показывает коэффициент детерминации? 14. Каков экономический смысл параметров в уравнении линейной парной корреляции? 15. Сделайте выводы по лабораторной работе. Таблица 8.3.
Лабораторная работа № 9
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 532; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.170.61 (0.011 с.) |


 - среднее значение результативного признака, b - вариация результативного признака на единицу факторного, a - теоретическое значение результативного признака при значении факторного, равное 0 (x=0), что на практике не имеет никакого экономического смысла.
- среднее значение результативного признака, b - вариация результативного признака на единицу факторного, a - теоретическое значение результативного признака при значении факторного, равное 0 (x=0), что на практике не имеет никакого экономического смысла. (8.1)
(8.1)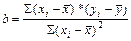 , тогда
, тогда  (8.2)
(8.2) (8.3)
(8.3) ) показывает, какая часть результативного признака обусловлена изменениями факторного:
) показывает, какая часть результативного признака обусловлена изменениями факторного: . Величина коэффициента корреляции колеблется в пределах:
. Величина коэффициента корреляции колеблется в пределах:  .
.
 10
10
 .
. и
и  , сравнение их с табличным значением
, сравнение их с табличным значением 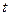 . Из вычислений следует, что минимальное значение факторного признака, при котором возможны изменения результативного равно 29 дней, а 65,699 % изменений затрат обусловлено изменениями возраста оборудования, 34,301 % изменений затрат обусловлено неучтёнными факторами, равенство коэффициента корреляции значению 0,811 говорит об очень сильной связи между изучаемыми признаками.
. Из вычислений следует, что минимальное значение факторного признака, при котором возможны изменения результативного равно 29 дней, а 65,699 % изменений затрат обусловлено изменениями возраста оборудования, 34,301 % изменений затрат обусловлено неучтёнными факторами, равенство коэффициента корреляции значению 0,811 говорит об очень сильной связи между изучаемыми признаками.