
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проверка гипотез относительно коэффициентов парной регрессииСодержание книги
Поиск на нашем сайте
Уравнение регрессии имеет вид:
Коэффициент b1 является коэффициентом регрессии. При проверке качества спецификации парной регрессии наиболее важной является задача установления наличия линейной зависимости между эндогенной переменной и регрессором модели. С этой целью проверяют значимость оценки параметра b. Алгоритм проверки значимости параметра b выполняется в следующей последовательности: 1) оценка параметров парной регрессии 2) оценка дисперсии возмущений 3) оценка 4) выбор значения tкр (по заданному уровню значимости альфа и числу степеней свободы (n-2) из таблиц распределения Стьюдента) 5) проверка неравенства Если данное неравенство выполняется, то регрессор признается незначимым, если не выполняется, то данная гипотеза отвергается и регрессор признается значимым, т.е. между эндогенной переменной и регрессором присутствует линейная зависимость.
При проведении экономического анализа перед исследователями очень часто возникает необходимость сравнить расчетные коэффициенты bo и b1 с некоторыми теоретическими коэффициентами βо и β1. Это сравнение осуществляется по схеме проверки гипотез. Предположим, проверяется гипотеза Но, состоящая в том, что эти величины совпадают. Но:=b1=β1. Тогда с ней конкурирующая гипотеза Н1: не совпадает. Для проверки таких гипотез рассчитывается t - статистика Стьюдента, которая при справедливости гипотезы Но имеет распределение Стьюдента с числом степеней свободы с парной регрессией
ν=n-2 (n-m-1) n – объем выборки m – кол-во объясняющих переменных Гипоеза Но б отклонена, если расчетное значение по модулю, т.к. нам безразлично в какую сторону произошло отклонение, окажется большим или равным величине, найденной из таблицы Стьюдента.
α-ур-нь значимости. Считается, что в эк задачах α может принимать значения 0,05 или 0,01, т.е. мы поверяем гипотезу с вероятностью 95 или 99%. α/2 берется в связи с тем, что отклоение может быть как отрицательным, так и положительным. При невыполнении этого условия считается, что нет оснований для отклонения гипотезы Но. Однако величины теоретических коэффициентов как правило неизвестны, поэтому на начальном этапе анализа рассматривается задача о наличие зависимости между факторами х и у. Эта проблема проверяется на основе гипотезы Но:b1=0 связи нет. С ней конкур-т H1:b1≠0 связь присутствует.
В такой постановке говорят, что проверяется гипотеза о статистической значимости коэффициента уравнения регрессии. Если приходится принять гипотезу Но, то мы говорим, что коэффициент незначим (слишком близок к 0) и соответствующую объясняющую переменную скорее всего из уравнения следует исключить. В противном случае коэффициент статистики значим. Н указывает на наличие определенной линейной зависимости между факторами. Тогда рассчитывается статистика Стьюдента по соотношению и по таблицам Стьюдента находят соответственно величину Если она ≤ расчет величины, то мы можем сказать, что есть основания отклонить гипотезу Но и принять Н1. Коэффициент отличен от 0. Для парной регрессии мы не будем проверять статистическую значимость bo, т.к. он только гарантирует прохождение линии регрессии ч/з ср точку выборки. Существует грубое правило, позволяющее делать первоначальные выводы о поведении коэффициентов уравнения при отсутствии таблиц Стьюдента. По нему сравнивается величина ошибки Sb1, допущенной при нахождении коэффициента с величиной этого коэффициента. А). Если стандартная ошибка > чем коэффициент, то 0<|tb1|≤1. В этом случае говорят, что коэффициент незначим. Б). Если ошибка не превосходит половины величины коэффициента, то 1<|tb1|≤2. Говорят, что коэффициент слабозначим. В). Если они соотносятся в диапазоне 2<|tb1|≤3, то коэффициент значим. Г). Если ошибка <1/3 коэффициента, то 3<|tb1|, коэффициент сильно значим. Это гарантия наличия практически линейной зависимости между изучаемыми факторами. Безусловно, на tb1 существенное влияние оказывает объем выборки n. Чем >n, тем <погрешность. Но при n>10 выписанное грубое правило оценки работает практически всегда.
|
|||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 383; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.147.67 (0.007 с.) |



 среднего квадратичного отклонения параметра b
среднего квадратичного отклонения параметра b при Н0: b=0
при Н0: b=0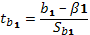

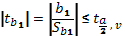
 .
.


