
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение границ доверительного интервалаСодержание книги
Поиск на нашем сайте
1) Находим оценки параметров спецификации (коэффициенты регрессии а^0, а^1, а^2, оценки среднеквадратичного отклонения коэффициентов регрессии Sa0, Sa1, Sa2 и т.д.):
2) Далее, выбираем строку и обозначаем ее прогнозом. Настоящее значение функции обозначим Yp. 3) Следующим шагом необходимо рассчитать прогнозное значение Y^p, используя полученные оценки коэффициентов регрессии (см. рисунок). В большинстве случаев налицо явное несовпадение результата и прогноза. Но ожидать точное совпадение прогноза и результата по меньшей мере наивно. Во-первых, Y^p - величина случайная, т.к. все три оценки коэффициентов a^0, a^1, a^2 вычислялись через значения случайной величины Y. Во-вторых, значение Yp содержит в себе неизвестное значение случайной составляющей εр. Все, что мы можем предпринять в этой ситуации, это проверить, попадают ли оба значения в доверительный интервал и делать заключение по этому факту. Величина доверительного интервала зависит от дисперсии прогноза, которая складывается из дисперсии εt - случайной составляющей эконометрической модели и дисперсии случайной величины оценки регрессии (уравнение регрессии), значения коэффициентов которой вычислены с помощью функции ЛИНЕЙН (см. рисунок). Однако оценки коэффициентов a^0, a^1, a^2 зависимы и для оценки их влияния на точность прогноза мало знать только их дисперсии, но нужно учесть и их взаимную зависимость, т.е. ковариацию, которая задается матрицей ковариаций. Матрица ковариации регрессии оценивается по следующей формуле: Cov(A^) = S2ε*(XT*X)-1, где A^ = (a^0, a^1, a^2)T, оценки коэффициентов регрессии; S2ε - дисперсия случайной составляющей ε. 4) Далее производим следующие вычисления: 1. (XT*X)-1. 2., где 5) Определим доверительный интервал для прогноза как (Y^p-tα*Sпрог, Y^p+tα*Sпрог), где tα-статистика Стьюдента, вычисляемая по формуле EXCEL СТЬЮДРАСПОБР. Если оба значения (т.е. Yp и Y^p) попадают в указанный интервал, то модель признается адекватной и пригодной для целей прогнозирования. Оценивание параметров модели взвешенным методом наименьших квадратов Для практики полезно из теоремы Гаусса-Маркова выделить частный случай обобщенного метода наименьших квадратов, разработанный Гауссом в первой половине 19в. В этом частном случае, именуемом в эконометрике взвешенным методом наименьших квадратов (ВМНК), матрица Это означает, что предпосылка
Введем здесь обозначение: Определение Согласно предположенной Гауссом терминологии С учетом (1) матрица оказывается диагональной:
В свою очередь свойство Модель Марковица Модель основана на том, что показатели доходности различных ценных бумаг взаимосвязаны: с ростом доходности одних бумаг наблюдается одновременный рост по другим бумагам, третьи остаются без изменения, а по четвертым доходность, наоборот, снижается. Такая зависимость не является детерминированной, т.е. однозначно определенной, а есть стохастической и называется корреляцией. Модель Марковица имеет следующие основные допущения: — в качестве доходности ценной бумаги принимается математическое ожидание доходности; — в качестве риска ценной бумаги принимается среднее квадратическое отклонение доходности; — принимается, что данные прошлых периодов, используемые при расчете доходности и риска, в полной мере отражают будущие значения доходности; — степень и характер взаимосвязи между ценными бумагами выражается коэффициентом линейной корреляции. По модели Марковица доходность портфеля ценных бумаг — это средневзвешенная доходность бумаг, его составляющих, и она определяется формулой:
Риск портфеля ценных бумаг определяется средним квадратическим отклонением доходности портфеля:
С использованием модели Марковица для расчета характеристик портфеля прямая задача приобретает вид:
Обратная задача представляется аналогичным образом:
При практическом применении модели Марковица для оптимизации фондового портфеля используются следующие формулы:
3) статистическая оценка коэффициента корреляции между показателями доходности двух ценными бумагами:
где Ясно, что для N рассматриваемых ценных бумаг необходимо рассчитать
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 489; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.184.250 (0.009 с.) |


 .
.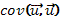 является диагональной, но не скалярной, т.е.
является диагональной, но не скалярной, т.е. 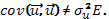
 справедлива, а предпосылка
справедлива, а предпосылка  нет, следовательно
нет, следовательно (1)
(1) (2)
(2) , определенная по правилу (2), называется весом случайной переменной
, определенная по правилу (2), называется весом случайной переменной  . Понятие веса случайной переменной позволяет придать внятный смысл константе
. Понятие веса случайной переменной позволяет придать внятный смысл константе 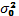 : это дисперсия такой случайной переменной, вес которой равен единице; иногда такую случайную переменную именуют (термин Гаусса) единицей веса.
: это дисперсия такой случайной переменной, вес которой равен единице; иногда такую случайную переменную именуют (термин Гаусса) единицей веса. в процедуре
в процедуре 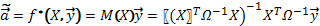
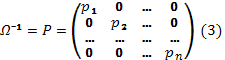 из формулы
из формулы  упрощается:
упрощается: 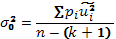
 обобщенных наименьших квадратов, справедливое для оценки Эйткена
обобщенных наименьших квадратов, справедливое для оценки Эйткена  =
=  Отметим, что матрицу (3) называют матрицей весов, а обратную к ней матрицу Ω – матрицей обратных весов или весовых коэффициентов.
Отметим, что матрицу (3) называют матрицей весов, а обратную к ней матрицу Ω – матрицей обратных весов или весовых коэффициентов. где N — количество ценных бумаг в портфеле;
где N — количество ценных бумаг в портфеле;  — процентная доля данной бумаги в портфеле;
— процентная доля данной бумаги в портфеле; 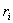 — доходность данной бумаги.
— доходность данной бумаги. , где
, где  ,
,  — процентные доли данных бумаг в портфеле;
— процентные доли данных бумаг в портфеле;  ,
,  — риск данных бумаг (среднеквадратическое отклонение);
— риск данных бумаг (среднеквадратическое отклонение);  —коэффициент линейной корреляции.
—коэффициент линейной корреляции.

 , где Т – количество прошлых наблюдений доходности данной ценной бумаги.
, где Т – количество прошлых наблюдений доходности данной ценной бумаги.
 ,
, — доходность ценных бумаг a и b в период t.
— доходность ценных бумаг a и b в период t. коэффициентов корреляции.
коэффициентов корреляции.


