
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Автокорреляция случайной составляющей. Тесты на наличие автокорреляцииСодержание книги
Поиск на нашем сайте
В классической регрессионной модели выполнение третьего условия Гаусса-Маркова (Соv(εt εS) = 0,при t ≠ s) гарантирует некоррелированность значений случайных членов в различные моменты наблюдений и это позволяет получить несмещенные МНК-оценки с минимальной дисперсией. Зависимость значений случайных членов в различные моменты времени называется автокорреляцией (сериальной корреляцией). Формальной причиной автокорреляции в регрессионных моделях является нарушение третьего условия теоремы Гаусса-Маркова, действительной же причиной может быть: неправильная спецификация переменных (пропуск важной объясняющей переменной); использование ошибочной функциональной зависимости, а иногда и характер наблюдений (например, временные ряды). Для проверки на автокорреляцию используется ряд критериев, из которых наиболее широкое применение получил критерий Дарбина-Уотсона(тест):
Критерий DW связан с выборочным коэффициентом корреляции между еt и еt-1, соотношением: DW≈2(1-r), Если автокорреляция отсутствует, то DW ≈ 2, при наличии положительной автокорреляции DW<2, если автокорреляция отрицательна, DW>2. И поскольку коэффициент корреляции принимает значения -1 ≤ r ≤ 1, то 0≤ DW ≤ 4. Полученное для данной регрессии значение статистики сравнивается с верхней и нижней границами ее критического значения dL ≤ dкрит ≤dU. Границы dU и dL выбираются из таблиц по числу наблюдений n, числу регрессоров k и уровню значимости α. При этом возможны следующие случаи: 1. Наличие положительной автокорреляции: DW<dL. 2. Наличие отрицательной автокорреляции: DW >4-dL. 3. Автокорреляция отсутствует: dU ≤ DW≤ 4-dU. Зоны неопределенности: dL<DW< dU или 4- dU <DW<4-dL. Графически можно определить:
22. Спецификация и преобразование к приведенной форме динамических моделей. Лаговые и предопределенные переменные динамической модели Из теории известно, что все переменные объекта изменяются со временем. Этот факт должен быть отражен в моделях. Для этого каждой переменной, которая изменяется со временем добавляется индекс “t”.
Определение. Экономические модели, значения переменных которых привязаны к моменту времени, называются динамическими. Определение. Переменные, связанные с моментом времени, называются датированными. Необходимость соотнесения переменных модели к моменту времени является одним из принципов спецификации модели. Дополнительно необходимо учесть, что - экономические объекты обладают инертностью, т.е. не все переменные объекта «успевают» за временем - не каждая переменная модели может быть известна в текущий момент времени. Например, производитель не может мгновенно реорганизовать производство, чтобы увеличить или уменьшить выпуск продукции в соответствии с изменившимся спросом, и он не знает, какой будет равновесная цена. Для учета этого факта в моделях применяются переменные, отнесенные к прошлому периоду времени, значения которых в текущий момент уже известны. Тогда приведенную выше модель следует записать в виде:
Где pt-1 - значение цены на продукцию в предыдущий период времени. Данная модель получила название «паутинная модель конкурентного рынка». Вторая часть вопроса. Определение. Переменные модели, отнесенные к предыдущим моментам времени, называются «лаговыми». Определение. Все лаговые переменные (эндогенные и экзогенные) и текущие экзогенные переменные составляют группу «предопределенных» переменных. Уточнение. В приведенной форме модели каждая текущая эндогенная переменная должна быть выражена через предопределенные переменные. В модели (2.2) второе уравнение получило приведенную форму на этапе спецификации. Для полного преобразование модели (2.2) к приведенной форме достаточно найти выражения для pt и Ydt:
Зная значения параметров модели и значение цены на товар в предшествующем периоде, можно дать прогноз равновесной цены и уровней спроса и предложения в текущем периоде времени Пример. Записать модель конкурентного рынка в приведенной форме
1. Выписываем необходимые вектора и матрицы для данной модели
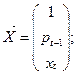 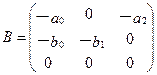 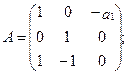 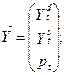
2. Вычисляем матрицу М Для этого находится обратная матрица А-1
Тогда матрица М есть:
Зная значения параметров модели и значение цены на товар в предшествующем периоде, можно дать прогноз равновесной цены и уровней спроса и предложения в текущем периоде времени
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 338; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.12.233 (0.006 с.) |

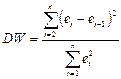

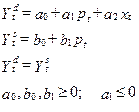 Например, Ydt означает, что переменная уровень спроса относится к текущему моменту времени. С учетом сказанного модель конкурентного рынка должна иметь вид:
Например, Ydt означает, что переменная уровень спроса относится к текущему моменту времени. С учетом сказанного модель конкурентного рынка должна иметь вид: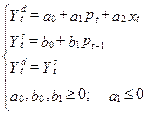
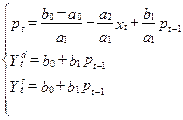
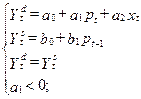
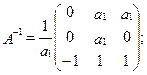
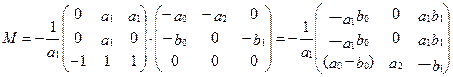
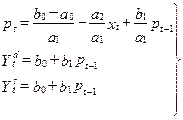 3. Приведенная форма модели принимает вид:
3. Приведенная форма модели принимает вид:



