
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Анализ вариации зависимой переменной в регрессииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Анализ вариации зависимой переменной в регрессии Рассмотрим вариацию (разброс) Разобьем эту вариацию на две части: объясненную регрессионным уравнением и не объясненную (т. е. связанную со случайной составляющей εt). Запишем разброс в виде следующего равенства:
И вариация
Рассмотрим последнее слагаемое. В него входит
Потому что
Поэтому верно равенство
Где
Тест Дарбина – Уотсона некоррелированности случайных возмущений в схеме Гаусса – Маркова Этот тест предназначен для проверки предпосылки о том, что
Неадекватность гипотезы влечет, очевидно, и неадекватность предпосылки. Часто истинной причиной отклонения гипотезы оказывается ошибка в выборе функции регрессии в спецификации модели, например пропуск значимой предопределенной переменной. Эмпирическая корреляция случайных остатков, порожденная этой причиной, называется ложной. Тест Дарбина – Уотсона позволяет идентифицировать, в частности, ложную корреляцию и поэтому рассматривается в эконометрике как один из наиболее важных тестов. Шаги теста: 1. Модель 2. Для проверки случайной последовательности на корреляцию используется критерий Дарбина-Уотсона Т.к. Из полученной формулы 3. Определяется интервал, в который попадает величина DW
Отметим, что тест Дарбина – Уотсона базируется на предположении, что: 1. Функция регрессии модели 2. Случайные остатки в уравнениях наблюдений 3. Предпосылки теоремы Гаусса – Маркова справедливы. Определение значений случайных остатков при нарушении равенства нулю их математического ожидания Значения ui(j) определяются по правилу ui(j)= Полученные значения ui (j) используются для получения оценочных значений, которые затем оценивают с помощью МНК. Сравниваем полученные оценочные значения a0 со значением исходного a0. В случае сильного отличия (больше ошибки) считается, что коэффициент a0 не обладает свойством несмещенности. Определение значений случайных остатков при нарушении предпосылки гомоскедантичности Значения ui(j) определяются по правилу ui(j)= Определение значений случайных остатков и объясняющей переменной при нарушении условия их некоррелированности Значения ui(j) определяются по правилу ui(j)= xi (j)= xi + ui(j), где xi значение объясняющей переменной, заданное вне модели. Модель Марковица Модель основана на том, что показатели доходности различных ценных бумаг взаимосвязаны: с ростом доходности одних бумаг наблюдается одновременный рост по другим бумагам, третьи остаются без изменения, а по четвертым доходность, наоборот, снижается. Такая зависимость не является детерминированной, т.е. однозначно определенной, а есть стохастической и называется корреляцией. Модель Марковица имеет следующие основные допущения: — в качестве доходности ценной бумаги принимается математическое ожидание доходности; — в качестве риска ценной бумаги принимается среднее квадратическое отклонение доходности; — принимается, что данные прошлых периодов, используемые при расчете доходности и риска, в полной мере отражают будущие значения доходности; — степень и характер взаимосвязи между ценными бумагами выражается коэффициентом линейной корреляции. По модели Марковица доходность портфеля ценных бумаг — это средневзвешенная доходность бумаг, его составляющих, и она определяется формулой:
Риск портфеля ценных бумаг определяется средним квадратическим отклонением доходности портфеля:
С использованием модели Марковица для расчета характеристик портфеля прямая задача приобретает вид:
Обратная задача представляется аналогичным образом:
При практическом применении модели Марковица для оптимизации фондового портфеля используются следующие формулы:
3) статистическая оценка коэффициента корреляции между показателями доходности двух ценными бумагами:
где Ясно, что для N рассматриваемых ценных бумаг необходимо рассчитать
Вторая часть вопроса. Определение. Переменные модели, отнесенные к предыдущим моментам времени, называются «лаговыми». Определение. Все лаговые переменные (эндогенные и экзогенные) и текущие экзогенные переменные составляют группу «предопределенных» переменных. Уточнение. В приведенной форме модели каждая текущая эндогенная переменная должна быть выражена через предопределенные переменные. В модели (2.2) второе уравнение получило приведенную форму на этапе спецификации. Для полного преобразование модели (2.2) к приведенной форме достаточно найти выражения для pt и Ydt:
Зная значения параметров модели и значение цены на товар в предшествующем периоде, можно дать прогноз равновесной цены и уровней спроса и предложения в текущем периоде времени Пример. Записать модель конкурентного рынка в приведенной форме
1. Выписываем необходимые вектора и матрицы для данной модели
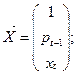 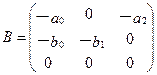 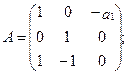 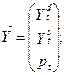
2. Вычисляем матрицу М Для этого находится обратная матрица А-1
Тогда матрица М есть:
Зная значения параметров модели и значение цены на товар в предшествующем периоде, можно дать прогноз равновесной цены и уровней спроса и предложения в текущем периоде времени Анализ вариации зависимой переменной в регрессии Рассмотрим вариацию (разброс) Разобьем эту вариацию на две части: объясненную регрессионным уравнением и не объясненную (т. е. связанную со случайной составляющей εt). Запишем разброс в виде следующего равенства:
И вариация
Рассмотрим последнее слагаемое. В него входит
Потому что
Поэтому верно равенство
Где
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 529; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.91.170 (0.007 с.) |

 значений
значений  вокруг среднего значения.
вокруг среднего значения.

 и тогда
и тогда
 - по определению,
- по определению,  по необходимому условию экстремума
по необходимому условию экстремума
 ,
, – это TSS, или весь разброс
– это TSS, или весь разброс – это ESS, или необъясненная часть
– это ESS, или необъясненная часть – это RSS, или объясненная часть
– это RSS, или объясненная часть теоремы Гаусса – Маркова, точнее, важнейшего частного случая этой предпосылки, а именно статистической гипотезы
теоремы Гаусса – Маркова, точнее, важнейшего частного случая этой предпосылки, а именно статистической гипотезы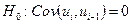 при j=i-1
при j=i-1 оценивается по уравнениям
оценивается по уравнениям  методом наименьших квадратов, рассчитываются по формуле
методом наименьших квадратов, рассчитываются по формуле  оценки остатков.
оценки остатков. Раскроем скобки и проведем преобразование исходной формулы:
Раскроем скобки и проведем преобразование исходной формулы: 
 r – выборочный коэффициент корреляции
r – выборочный коэффициент корреляции следует, что если r =0 (корреляция отсутствует), то DW=2; если корреляция положительна, то DW < 2; если отрицательна - DW > 2. Так как коэффициент корреляции
следует, что если r =0 (корреляция отсутствует), то DW=2; если корреляция положительна, то DW < 2; если отрицательна - DW > 2. Так как коэффициент корреляции  Поскольку критическое значение dкр невозможно табулировать по ряду причин, граница раздвигается и значения левой границы dL и правой границы dU выбираются из таблицы в зависимости от числа наблюдений n, числа независимых переменных k и уровня значимости α. Следовательно, по таблицам Дарбина-Уодсона выбирают 2 константы
Поскольку критическое значение dкр невозможно табулировать по ряду причин, граница раздвигается и значения левой границы dL и правой границы dU выбираются из таблицы в зависимости от числа наблюдений n, числа независимых переменных k и уровня значимости α. Следовательно, по таблицам Дарбина-Уодсона выбирают 2 константы  и
и  , по аргументам 1)
, по аргументам 1)  2)
2)  3)
3) 

 подлежит определению)
подлежит определению) i ui*(j)+mi, но константы mi
i ui*(j)+mi, но константы mi  0 при всех i=1,2...n
0 при всех i=1,2...n i ui*(j)+mi, но величины
i ui*(j)+mi, но величины 
 где N — количество ценных бумаг в портфеле;
где N — количество ценных бумаг в портфеле;  — процентная доля данной бумаги в портфеле;
— процентная доля данной бумаги в портфеле;  — доходность данной бумаги.
— доходность данной бумаги. , где
, где  ,
,  — процентные доли данных бумаг в портфеле;
— процентные доли данных бумаг в портфеле;  ,
,  — риск данных бумаг (среднеквадратическое отклонение);
— риск данных бумаг (среднеквадратическое отклонение);  —коэффициент линейной корреляции.
—коэффициент линейной корреляции.

 , где Т – количество прошлых наблюдений доходности данной ценной бумаги.
, где Т – количество прошлых наблюдений доходности данной ценной бумаги.
 ,
, — доходность ценных бумаг a и b в период t.
— доходность ценных бумаг a и b в период t. коэффициентов корреляции.
коэффициентов корреляции.
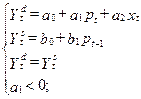
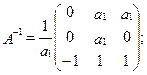
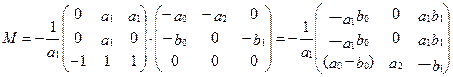
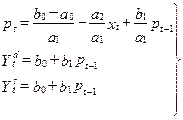 3. Приведенная форма модели принимает вид:
3. Приведенная форма модели принимает вид:



