
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие случайной переменной. Ее математическое ожидание (М. О. ).Содержание книги
Поиск на нашем сайте
Случайная переменная - это любая переменная значение которой, не может быть точно предсказано. М.О-ие случайной величины- это взвешенное среднее всех ее возможных значений. При этом в качестве весового коэффициента берется вероятность соответствующего исхода. Пусть случайная величина может принимать некоторые значения (E1,E2, …,En) и вероятность их получения равна (р1,р2,…,рn).Тогда М.О. случайной переменной определяется след.образом: (3.1) Правила расчета М.О. Существуют следующие правила расчета М.О.: Правило1: М.О. суммы нескольких переменных равно сумме их М.О-ий: (3.2)
Правило 2: если случайную величину умножить на константу, то ее М.О-ие увеличится во столько же раз. Е(а´ε)= а´Е(ε) (3.3) Правило 3: М.О. константы - есть она сама: F(a)=a (3.4) Ре условия Гаус Маркова. Для того чтобы анализ, основанный на методе наименьших квадратов давал лучшие результаты, необходимо выполнение условия Гас- Маркова для случайных составляющих: 1. М.О. случайного члена в любом наблюдении должно быть равно нулю: Е(εi)= 0 В некоторых ситуациях случайный член будет положительным иногда отрицательным, но он не должен иметь систематического смещения не в 1-ом из направлений. Если уравнение регрессии включает постоянный член, то это условие выполняется автоматически. Т.к. роль константы состоит в том, чтобы определить любую тенденцию, в которой не учитывают объясняющие переменные, включенные в уравнение регрессии. 2. Дисперсия случ. члена должна быть постоянна для всех наблюдений. pop.var (Ei)- теоретическая вариация. (3.6) pop.var(Ei) = 3. Это условие предполагает отсутствие системной связи между значениями случайного члена в любых 2-ух наблюдениях.
(3.7) Т.е. если случ. член велик и положителен в олном наблюдении, это не обуславливает тенденцию к тому, что он будет большим и положительным в другом наблюдении. Случ. члены должны быть независемы друг от друга. 4. С.ч-н должен быть независимо распределен от объясняющей переменной. Значение независимой переменной в каждом наблюдении должно считаться полностью определенным внешними причинами, которые не учитываются в уравнении регрессии. Если условие выполняется, то теоретическая вариация между независимой переменной и случ. членом равна 0. Pop var (xi, εi)=0 (3.8)
18.Условия гомо и гетероскедастич-сти. Последствия гетероске-сти. Первые два условия Гаус Маркова указывают, что случайные члены появ-ся на основе вероят-тных распреде-й, имеющих нолевое мат-кое ожидание и одну и ту же дисперсию. Их факти-кие знач-я иногда будут полож-ми, иногда отриц-ми, но но они не будут иметь сильных отклонений в любом наблю-ии, т.е вероят-ть того, что величина e примет какое-то значение, будет одинаковой для всех наблюде-й. Здесь имеет место условие гомоскедастич-ти:Ф(3.6) одинакова для всех i. Вместе с тем возможно, что теори-ское распред-е случайного члена яв-ся разным для различ-х наблюд-й выборки. Это не означает, что слячайный член будет иметь особенно большие отклонения в конце выборки, но вероят-сть их получения будет высокая, т.е имеет место условие гетероскедаст-ти: Ф(3.6) не одинакова для всех. Рис. 1- Различия м/д гомо и гетероскедас-тью. На рис.2 показано, как будет выглядеть характерная диаграмма распределения ф-ции y(x), если имеет место гетероскедаст-сть. Рис.2-Влияние гетероскед-сти на распредел-е ф-ции y(x). При отсутствии гетероскед-сти коэф-ты регрессии имеют наиболее низкую дисперсию среди несмещенных оценок. Если имеет место гетероскед- сть, то оценки метода наименьших квадратов будут не эфф-ны. Гетероскед-сть становится проблемой, когда значение переменных, входящих в уровни регрессии значительно различается в разных наблюдениях. Если истинная зависимость описывается уравнением прямой, то при нем экон-ие переменные меняют свой масштаб одновременно,то изменение значений, не включаемых переменных и ошибки измерения, влияя совместно на случайный член делает его сравнительно малым при больших X и Y. Гетероске- сть может также появляться при анализе временных рядов. 19.Обнаружение гетероскедастичности.Тест ранговой корреляции Спирмена, тест Глейзера. Проявление проблем гетероскед-сти можно предвидеть основываясь на знаниях характера данных. В этих случаях можно предпринимать действия на этапе спецификации модели регрессии. Это позволит уменьшить или устранить необходимость формальной проверки. В настоящее время используются следующие виды тестов гетероскед-сти, в которых делается предположение о наличие зависимости между дисперсией случайного члена и величиной объясняющей переменной: 1)Тест ранговой корреляции Спирмена.
При его выполнении предполагается, что дисперсия случайного члена будет либо увеличиваться, либо уменьшаться по мере увеличения X и поэтому в регрессии, оцениваемой с помощью метода наименьших квадратов абсолютные величины остатков и значение X будут коррелированны. Данные по X и остатки упорядочиваются, а затем определяется коэффициент ранговой корреляции: Ф(3.9), Где Дi- разность между рангом X и рангом е, е- остатки(отклонение) фактических значений Y от теоретических значений. Тест Глейзера. Чтобы использовать данный метод следует оценить регрессионную зависимость y(x) с помощью обычного метода наименьших квадратов, а затем вычислить абсолютные величины остатков еi по модулю, оценив их регрессию. 20.Обнаружение гетероскед-сти. Тест Голдфельда Квандта. Появление проблем гетероскед-сти можно предвидеть основываясь на знаниях характера данных. В этих случаях можно предпринимать действия на этапе спецификации модели регрессии. Это позволит уменьшить или устранить необходимость формальной проверки. В настоящее время используются следующие виды тестов гетероскед-сти, в которых делается предположение о наличие зависимости между дисперсией случайного члена и величиной объясняющей переменной: 1)Тест Голдфельда Квандта. При проведении проверки по этому критерию предполагается, что дисперсия случайного члена пропорциональна значению X в этом наблюдении. Предполагается, что случайный член распределен нормально и не подвержен автокорреляции. Все наблюдения в выборке упорядочиваются по величине X, после чего оцениваются отдельные регрессии для первых n 21. Автокорреляция и ее факторы. Автокорреляция в регрессионном анализе обычно встречается при исследовании временных рядов. Постоянная направленность воздействия не включенных в уравнении переменных является наиболее частой причиной появления положительной автокорреляции. Пример1: При оценке спроса на мороженное по ежемесячным данным предполагается, что состояние погоды является единственным важным фактором. При этом проводятся ряд наблюдений, когда теплая погода способствует увеличению спроса, а холодная погода наоборот. Если доход возрастает со временем, то схема наблюдений будет выглядеть след. Образом: Рисунок3 – Положения автокорреляции. Изменения эконом-кой конъюнктуры приводит к положительным результатам и в анализе. Автокорреляция является существенной проблемой, когда интервал между наблюдениями имеет небольшую величину. Чем больше этот интервал, тем меньше вероятность того, что при переходе от одного наблюдения к другому характер влияния неучтенных факторов будет сохраняться.
Автокорреляция может быть отрицательной. Это означает, что корреляция между последовательными значениями случайного члена отрицательна, т.е за положит-ным значением в одном наблюдении следует отриц-ное значение в другом. Тогда диаграмма распределения выглядит след.образом: Рисунок4- Отрицательная автокорреляция. В экономике отрицательная автокорреляция встречается редко, но иногда она появляется при преобразовании первоначальных моделей в форму, подходящую для регрессионного анализа.
|
|||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 207; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.174.4 (0.009 с.) |

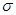 ^2Ei -одинакова для всех i. (3.6) Если рассматриваемое условие не выполняется, то коэффициенты регрессии будут не эффективны.
^2Ei -одинакова для всех i. (3.6) Если рассматриваемое условие не выполняется, то коэффициенты регрессии будут не эффективны. 
 со штрихом наблюдений и для последних n
со штрихом наблюдений и для последних n 


