Социально-экономические явления представляют собой результат одновременного воздействия большёго количества внешних и внутренних причин.

Связи между явлениями классифицируются по ряду оснований. Признаки по их значению делятся на 2 класса:

1. Признаки, обуславливающие изменения других признаков, связанных с ними, называются факторными.

2. Признаки, изменяющиеся под воздействием факторных, называются результативными.

Связи между явлениями классифицируются по степени тесноты, по направлению и по аналитическому выравниванию.

По степени тесноты:

- функциональная связь – это связь, при которой определённому значению факторного признака соответствует только одно значение результативного признака;

- если причинная зависимость проявляется не в каждом отдельном случае, а в общем среднем, при небольшом количестве наблюдений, то связь наз. стохастической. Частным случаем стохастической связи является корреляционная связь, при которой изменение значений результативного признака обусловлено изменением факторных признаков.

По направлению связи:

- прямая, при которой с увеличением или уменьшением значений факторного признака происходит увеличение или уменьшение результативного признака;

- обратная, при которой факторный и результативный признаки изменяются в противоположных направлениях.

По аналитическому выравниванию:

- линейные связи, если связь между явлениями приближено выражена уравнением прямой;

- нелинейные связи, если связь между явлениями выражена уравнением кривой.

9. Парная регрессия

Парная регрессия характеризует связь между двумя признаками. Аналитически связь между ними описывается следующими уравнениями:

- прямой Y(X)=A₀ + A₁*X параболыY(X)=A₀+A₁*X+A₂*X

-гиперболы Y(X)=A₀+A₁+ 1/X

Определить тип уравнения можно в первую очередь графическим способом. Помимо этого существует более общее указание: если результативный и факторный признаки возрастают одинаково, то это свидетельствует о наличии линейной связи между ними. Если результативный признак увеличивается в арифметической прогрессии, а факторный значительно быстрее, то используется параболическая функция.

10. Метод наименьших квадратов Оценка параметров уравнения А₀ , А₁, А₂ осуществляется методом наименьших квадратов (МНК). В основе которого лежит предположение о независимости наблюдений исследуемой совокупности и нахождении параметра модели, при котором минимизируется сумма квадратов отклонений фактических значений результативного признака от теоретических, полученных по уравнению регрессии.

S=∑ (Y_I – Y(X))²→MIN.2)

Система нормальных уравнений для нахождения параметров линейной парной регрессии методом наименьших квадратов имеет след. вид:

N*A₀ + A₁*∑X = ∑Y

A₀*∑X+A₁*∑X²=∑X*Y (2.3)

N- объём исследуемой совокупности.

В уравнении регрессии параметр А₀ показывает усреднённое влияние на результативный признак неучтённых факторов.

Параметр А₁ (А₂) – коэффициент регрессии, показывает на сколько изменяется в среднем значение результативного признака при изменении факторного на единицу в его собственном измерении.

Если связь между признаками криволинейная и описывается уравнением параболы, то система нормальных уравнений будет иметь следующий вид:

N*A₀ + A₁*∑X + A₂*∑X² = ∑Y,

A₀*∑X+A₁*∑X²+A₂*∑X³=∑XYA₀*∑X²+A₁*∑X³+A₂*∑X⁴= ∑X²Y (2.4)

Оценка обратной зависимости между Х и У осуществляется на основе уравнения гиперболы. Тогда система нормальных уравнений выглядит так: N*A₀ + A₁*∑1/X = ∑X

A₀*∑1/X + A₁∑1/X² = ∑Y/X

11. Множественная регрессия Изучение связи между тремя и более связанными между собой признаками носит название множественной регрессии. Она описывается функцией следующего вида:

Y_1,2,….K=F(X₁, X₂,…..X_K) (2.6)

Построение моделей множественной регрессии включает следующие этапы:

1. Выбор формы связи.

2. Выбор факторных признаков.

3. Обеспечение достаточного объёма совокупности для получения несмещённых оценок.

Выбор типа уравнения затрудняется тем, что для любой формы зависимости можно выбрать целый ряд уравнений, которые эти связи будут описывать.

Практика построения многофакторных моделей показывает, что все реально существующие зависимости между социально-экономическими можно описать используя 5 типов моделей.

1. Линейная Y(X)=A₀+A₁*X₁+A₂*X₂+…+A_K*X_K (2.7)

2. Степенная Y(X)=A₀*X₁^A1*X₂^A2*…*X_K^AK (2.8)

3. Показательная Y(X)=e^{A0+A1*X1+A2*X2+…+Ak*Xk} (2.9)

4. Параболическая Y(X)=A₀+A₁*X₁²+A₂*X₂²+…+A_K*X_K² (2.10)

5. Гиперболическая Y(X)=A₀+A₁*1/X₁+A₂*1/X₂+…+A_K*1/X_K (2.11)

Основное значение имеют линейные уравнения в силу их простоты и логичности экономической интерпретации.

 

12.Проблемы построения модели регрессии. Пути их преодоления. Важнейшим этапом построения выбранного уравнения множественной регрессии является отбор и последующее включение факторных признаков. Проблема отбора факторных признаков может быть решена на основе интуитивно-логических или многомерных методов анализа. Наиболее приемлемым способом является ШАГОВАЯ РЕГРЕССИЯ. Сущность этого метода заключается в последовательном включении факторов в уравнение регрессии и последующей их проверке на значимость. Факторы поочерёдно вводятся в уравнение прямым методом. При поверке на значимость определяется на сколько уменьшается сумма квадратов остатков и увеличивается величина множественного коэффициента корреляции.

При построении модели регрессии можно столкнуться с проблемой мультиколлинеарности, под которой понимается тесная зависимость между факторными признаками, включёнными в модель. Данная проблема существенно влияет на результаты исследования. Устранить её можно, исключив из корреляционной модели один или несколько линейно связанных факторов или преобразовав исходные признаки в новые укрупнённые факторы.

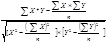13. Оценка существенности корреляционной зависимости. Измерение тесноты и направленности связи является важной задачей корреляционно-регрессионного анализа. Теснота связи при линейной зависимости измеряется с помощью линейного коэффициента корреляции: R= (2.12) Значимость линейного коэффициента корреляции проверяется на основе t-критерия Стьюдента, то есть определяется расчётное значение данного показателя: 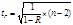(2.13) Если t_р больше t_таб, то это свидетельствует о наличии зависимости между изучаемыми признаками. Теснота связи при криволинейной зависимости измеряется с помощью эмпирического корреляционного отношения: η= 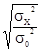(2.14) где 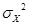-факторная дисперсия, которая показывает вариацию результативного признака под влиянием факторного признака.

 

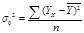(2.15) 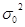-общая дисперсия, которая показывает вариацию результативного признака под влиянием всех факторов. 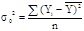(2.16) Множественный коэффициент корреляции определяется при наличии линейной связи между результативным и несколькими факторными признаками: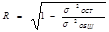

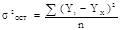
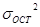где -остаточная дисперсия, которая показывает вариацию результативного признака под влиянием неучтённых факторов. Проверка значимости множественного коэффициента корреляции определяется на основе F-критерия Стьюдента. 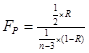(2.19) 14. ПРОВЕРКА АДЕКВАТНОСТИ РЕГРЕССИОННЫХ МОДЕЛЕЙ. Проверка адекватности моделей, построенных на основе уравнения регрессии начинается с оценки значимости каждого коэффициента регрессии, т. е. Определяется расчётное значение t-критерия Стьюдента.

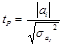(2.20) 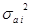-дисперсия коэффициента регрессии

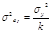Если t расчётное больше t табличного при (α; V=n-k-1), где α - уровень значимости, V=n-k-1 число степеней свободы. (2.21)

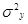где - дисперсия результативного признака,

k – количество объясняющих переменных.

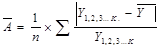Проверка адекватности этой модели осуществляется с помощью расчёта средней ошибки аппроксимации (2.22)

Величина данной ошибки не должна превышать 15 %.