Анализ случайных остатков в модели регрессии

 

Остатки представляют собой независимые случайные величины, которые включают влияние не учтенных в модели факторов, случайных ошибок и особенностей измерения. Их анализ проводится после построения уравнения регрессии. Случайные остатки должны отвечать определенным критериям: быть несмещенными, состоятельными и эффективными.

- несмещенность является желательным свойством, так как только при ней остатки имеют практическую значимость. Несмещенность оценки означает, что математическое ожидание остатков равно нулю. То есть при большом объеме выборки средняя величина остатков будет стремится к нулю, и параметр можно будет рассматривать как среднюю величину.

- оценки считаются эффективными, если они характеризуются наименьшей дисперсией.

- состоятельность оценок характеризует увеличение их точности с увеличением объема выборки. Большой практический интерес представляет та вероятность получения оценки на заданном расстоянии от истинного значения параметра, которая близка к единице.

Условия для получения подобных оценок представляют собой предпосылки МНК:

- случайный характер остатков,

- нулевая средняя величина остатков, не зависящая от фактора,

- гомоскедастичность - дисперсия каждого отклонения одинакова для всех значений х,

- отсутствие автокорреляционных остатков - распределение остатков независимо друг от друга,

- остатки подчиняются нормальному распределению.

 

26. использование коэффициента ранговой корреляции Спирмена для выявления гетероскедастичности случайных остатков:

Суть проверки заключается в том, что в случае гетероскедастичности абсолютные остатки коррелированны со значениями фактора. Эту корреляцию можно измерить с помощью коэффициента ранговой корреляции Спирмена: где, d – абсолютная разность между рангами значений фактора и остатка. Статистическую значимость можно оценить с помощью t-критерия: . Если это значение больше табличного, то корреляция между остатком и фактором статистически значима, то есть имеет место гетероскедастичность остатков. В противном случае принимается гипотеза об ее отсутствии.

 

27. отбор факторов в модель множественной регрессии: требования к факторам, методы отбора: множественная регрессия представляет собой модель, где среднее значение результата рассматривается как функция нескольких независимых факторов. Включение в уравнение того или иного набора факторов связано прежде всего с представлениями о взаимосвязи результата и явлений. Теоретически регрессионная модель позволяет учесть любое количество факторов, но практически в этом нет смысла. Включаемые в регрессию факторы должны объяснять вариацию зависимой переменной, то есть уменьшать долю остаточной дисперсии. Факторы, включаемые в множественную регрессию, должны отвечать следующим требованиям:

- быть количественно измеримыми. Качественный фактор может быть включен в модель после придания ему количественной определенности (баллы, ранжирование).

- не должны быть коррелированны между собой и тем более находится в точной функциональной связи. Включение таких факторов может привести к ненадежности оценок коэффициентов регрессии. Если факторы сильно коррелированны, нельзя определить их изолированное влияние на результат, то есть параметры становятся неинтерпретируемыми.

Лишние факторы приводят к статистической незначимости параметров регрессии по критерию Стьюдента. Отбор факторов обычно производится в две стадии: отбор факторов исходя из сути проблемы; отбор на основе матрицы показателей корреляции и определения t-критериев для параметров регрессии.

1) Коэффициенты интеркорреляции позволяют исключать дублирующие факторы (переменные коллинеарны, если коэффициент больше 0,7). Предпочтение в данном случае отдается тому фактору, который имеет наименьшую тесноту связи с другими факторами. Матрица парных коэффициент корреляции играет большую роль в отборе, но парные коэффициенты не могут полностью решить задачу. Эту роль выполняют показатели частной корреляции, оценивающие в чистом виде тесноту связи фактора и результата.

2) Наибольшую трудность представляет мультиколлениарность факторов. Коэффициенты множественной детерминации позволяют выявить такие переменные. Чем ближе значение коэффициента к 1, тем сильнее проявляется мультиколлениарность факторов.

3) Существуют пути преобразование факторов, которые позволяют уменьшить корреляцию факторов.

- переход к совмещенным уравнениям регрессии, которые отражают не только влияние факторов, но и их взаимодействие. Такие уравнения строятся, например, при исследовании эффекта влияния на урожайность разных видов удобрений.

- переход к уравнения приведенной формы, где рассматриваемый фактор выражается из другого уравнения. Например, для регрессии с двумя факторами, если исключить один фактор, то мы придем к парной регрессии.

Выделяют следующие основные методы: метод исключения (отсев факторов из полного набора), метод включения (дополнительное введение фактора), шаговый регрессионный анализ (исключение ранее введенного фактора).

 

 

28. прогнозирование по уравнению регрессии (на примере парной линейной регрессии):

В прогнозных расчетах по уравнению регрессии определяется предсказываемое значение как точечный прогноз при , то есть путем подстановки в линейное уравнение регрессии соответствующего значения х. однако точечный прогноз невозможен, поэтому он дополняется расчетом стандартной ошибки прогнозного значения и соответственно мы получаем интервальную оценку прогнозного значения.,. Рассмотренная формула стандартной ошибки предсказываемого среднего значения результата при заданном значении фактора характеризует ошибку положения линии регрессии. Величина стандартной ошибки достигает минимума при х равном среднему значению и возрастает по мере того, как удаляется от среднего х в любом направлении.

 

 

29. особенности нахождения параметров для нелинейных функций регрессии:

Параметры для нелинейной регрессии определяются, как и в линейной, методом наименьших квадратов, так как эти функции линейны по параметрам. Например, для параболы , заменив переменные , получим двухфакторное уравнение линейной регрессии: , для оценки параметров которого используется МНК. то есть любое подобное уравнение сводится к линейной регрессии с ее методами оценивания параметров и проверки гипотез.

 

Формула коэффициента детерминации не изменяется. Причина расчета показателей тесноты связи только для линеаризованных функций – это выполнение правила сложения дисперсий, на основе которого построен этот показатель. Для нелинейных функций показатели тесноты связи называются индексами, то есть индекс детерминации, индекс корреляции.

- индекс корреляции: имеет ту же интерпретацию что и коэффициент корреляции.

- индекс детерминации представляет собой квадрат индекса корреляции. Так как в нем используется соотношение факторной и общей суммы квадратов отклонений, индекс детерминации имеет тот же смысл, что и коэффициент детерминации. Значение коэффициента детерминации показывает, на сколько процентов вариация результата обусловлена вариацией фактора, включенного в уравнении регрессии. Соответственно 1- R^2 – характеризует, на сколько вариация обусловлена вариацией других факторов, не учтенных в модели. Используется для проверки статистической значимости в целом уравнения нелинейной регрессии по Фишеру. Близость показателей r^2 и R^2 означает, что нет необходимости усложнять форму уравнения и можно использовать линейную функцию.

 

10. использование мнк для нахождения параметров парной линейной регрессии:

МНК применяется для нахождения параметров уравнения регрессии, если выполняются предпосылки классической нормальной линейной модели, которые часто называют предпосылками МНК. МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений фактических от значений расчетных минимальна, то есть линия регрессии выбирается так, чтобы сумма квадратов расстояний по вертикали между точками и этой линией была бы минимальной: . Для того, чтобы найти минимум функции, надо вычислить производные по каждому из параметров и приравнять их к нулю. Преобразовав, получим: . 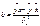Решая систему (деля первое уравнение на n), получаем: и .