Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Идентификация системы эконометрических уравнений. Необходимое условие.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Проблема наличия у системы решений называется проблемой идентификации системы. Проверка идентификации, т.е. проверка системы на возможность её решения производятся с помощью необходимого и достаточного условий идентификации. Проверка представляет собой проверку каждого уравнения системы на идентификацию, затем делается выбор об идентификации всей системы. Проверка на идентификацию не осуществляется для тождеств, хотя сами тождества принимают участие в проверке. Необходимым условием является: 1. Проверка уравнений: необходимо определить следующие величины: · количество эндогенных переменных, входящих в данное уравнение (H); · количество предопределённых переменных, отсутствующих в данном уравнении (D); · сравниваются величины H и D+1 o > - уравнение не идентифицируется; o < - точно идентифицируется; o = - сверхидентифицируемая. 2. Выводы по системе: Есть ли неидентифицируемые уравнения? Да – система неидентифицируется Нет – есть ли сверхидентифицируемые уравнения? Да – система сревхидентифицируема Нет - система точно идентифицируема
Идентификация системы эконометрических уравнений. Достаточное условие идентификации системы эконометрических уравнений
Проверка ур-я: - Необходимо выявить переем-е, кот-е не входят в это ур-е - Для этих переем-х форм-ся матрица коэф при них, строки матрицы соовт-т всем другим ур-м и тожд-м сис-мы, столбцы соотв-т конкретным перем-м. Если переем-я стоит в левой части ур-я, т.е. явл-ся рез-м, то коэф при ней равен «-1» и в тождествах коэф-ты при факторах равны «+1» - Определяется ранг этой матрицы (Из матрицы необходимо выделить квадрат максимального размера, где число строк и столбцов равны. Затем ищем определитель матрицы. Если удается выделить такую квадр. матр.(хотя бы одну), где определитель не равен 0, то ранг матрицы равен длине стороны этой матрицы. Если нет, то размерность этой матрицы сокращают) Для выполнения достаточного условия ранг матрицы должен быть ≥ количеству эндогенных пер-х в сис-ме (-1).
Косвенный МНК Этот метод используется, если система точно идентифицируема. Решение: - Необходимо построить ПФМ и для каждого уравнения ПФМ найти парам-ры с помощью МНК - После нахождения парам-ов ур-я стар-ся преобразовать таким образом, чтобы получить уравнение, имеющее ту же стру-ру, что и ур-е СФМ. Успешный рез-т этих преобр-й является решением.
Двухшаговый МНК Этот метод используется, если система сверхидентифицируема. - Необходимо построить ПФМ и для каждого уравнения ПФМ найти парам-ры с помощью МНК - Для каждого ур-я СФМ (исходной модели) выпол-ся след. действие: 1. Находят эндогенные перем-е, явл-ся в дан. уравнении факторами 2. Испол-я ПФМ, рассчит-т выровнен-е значения переменных, выявл-я в предыдущем пункте (yˆ) 3. К рассматр-му ур-ю СФМ прим. МНК, причем вместо наблюд-х фактич. знач- эндоген. перм-х факторов берут выровнен-е значен-я, рассчит. в предыдущем пункте.
Ошибка аппроксимации
Средняя ошибка аппроксимации
Общая вариация
Факторная вариация
Остаточная вариация
Стандартная ошибка уравнения
СКО
Свободный член
Коэффициент регрессии
Дисперсия
Коэффициент эластичности
Сводный коэффициент эластичности
Парный линейный коэффициент корреляции
Теоретическое корреляционное отношение
Индекс корреляции
оценка значимости коэффициента регрессии (для линейной однофакторной модели): - нулевая теория
- остаточная дисперсия на 1 степень свободы - t-статистика, t-критерий Стьюдента. - t <>
- доверительный интервал
оценка статистической значимости уравнения регрессии - нулевая теория H0: r2 = 0 (R2 = 0)- отсутствие связи между признаками H1: r2 = 0 (R2 = 0) - F-критерий Фишера
оценка статистической значимости коэффициента корреляции
оценка статистической значимости в множественной регрессии: Частный критерий Фишера
стандартизация:
Частное уравнение регрессии
|
||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 773; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.79.214 (0.009 с.) |




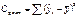





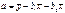

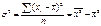









 H0:
H0: 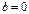 H1:
H1: 
 - определяется стандартная ошибка коэффициента регрессии
- определяется стандартная ошибка коэффициента регрессии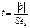
 ;
;  < t – гипотеза отклоняется, коэффициент значим.
< t – гипотеза отклоняется, коэффициент значим.

 - число степеней свободы для факторной дисперсии,
- число степеней свободы для факторной дисперсии,  - для остаточной.
- для остаточной.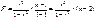

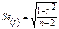
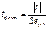
 используется при условии что
используется при условии что  а
а 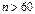 . В других случаях используется Z статистика.
. В других случаях используется Z статистика.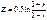

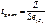


 - прирост степеней свободы (=1 при добавлении 1фактора)
- прирост степеней свободы (=1 при добавлении 1фактора) - натуральное уравнение
- натуральное уравнение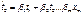 - стандартизированное уравнение (без свободного члена)
- стандартизированное уравнение (без свободного члена)




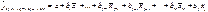 астный коэффициент эластичности
астный коэффициент эластичности