Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Предмет эконометрики, её связь с другими наукамиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Предмет эконометрики, её связь с другими науками Термин «эконометрика» возник в 20 веке и изучает количественные и качественные экономические взаимосвязи с помощью математических и статистических методов и моделей. Эконометрика- это наука, изучающая количественные закономерности экономических явлений и процессов, с помощью статистических методов и моделей. Эконометрика дает инструментарий для экономических измерений, а также методологию оценки параметров моделей микро и макроэкономики. Кроме того, эконометрика активно используется для прогнозирования экономических процессов как в масштабах экономики в целом, так и на уровне отдельных предприятий. Эконометрика входит в обширное семейство дисциплин, посвященных измерениям и применению статистических методов в различных областях науки и практики. К этому семейству относятся, в частности, биометрия, наукометрия, психометрия, хемометрия, квалиметрия. Особняком стоит социометрия — этот термин закрепился за статистическими методами анализа взаимоотношений в малых группах, то есть за небольшой частью такой дисциплины, как статистический анализ в социологии
Этапы эконометрического исследования. 1. Постановка проблемы. 2. Получение данных и анализ их качества. Данные должны быть получены по однородной совокупности и не смешивать явления. 3. Спецификация модели. Спецификация – выбор показателей и конкретной модели (конкретных показателей которые будут исследованы, выбор определенной модели решения.) Она тесно связана с постановкой проблемы. 4. Оценка параметров модели. Некоторые параметры являются константами. y = a+bx; a и b - параметры, y и x –переменные. Данные обладают свойствами как, ошибки наблюдения и ошибки выборочного наблюдения. Все данные являются выборочными полученные на 2-ом этапе, поэтому параметры модели рассчитанные по этим данным являются не точными значениями этих (истинных) параметров, а их оценкой. Кроме самих параметров на этом этапе оцениваются их качество. 5. Интерпретация и использование результатов исследования (прогнозирование) Виды эконометрических моделей.
Эконометрические модели можно классифицировать по: Видам связей между показателями. А) Стахастические – эти связи имеют элемент случайности. Частный случай стахастических связей - это корреляционные связи. Корреляционная связь – это связь при котором конкретным значением фактора соответствует определенные средние значения результата, т.е. функциональные зависимости. Например: средняя стоимость проезда зависит от расстояния, значение результата, которое было рассчитано по модели отражающую корреляционную связь, путем подстановки в нее значения факторов, называется выровненным или теоретическим значением результата и обозначается ŷ Отклонение фактического значения результата от выравненного, определяется случайными факторами. Не может быть точно рассчитано заранее до проведения наблюдения, называемое отклонение – есть случайный остаток или случайное отклонение (ошибка) и обозначается ε y = a + bx + ε
ŷ = a + bx y = ŷ + ε Модель включает в себя регрессию и может включать тождество Б) Функциональные – это связи где значение одних показателей однозначно определяет значение других показателей. Те показатели которые оказывают влияние называются независимыми переменными – факторы(х) Показатели на которые оказывается влияние называются зависимые переменные – результатами(у) Частный случай функции связи: y = x + z, z – тоже фактор. y-доход, x- расход, z- накопление. Такое выражение называется тождеством, в нем все параметры известны. 2. По количеству уравнений входящих в эконометрическую модель. Модель может состоять из одного уравнения – регрессии, или нескольких уравнений – система эконометрических уравнений. 3.По форме функции использованной в регрессии. Соответственно различают линейные и нелинейные регрессии. 4.По количеству факторов входящих в уравнение регрессии. С одним фактором – парная регрессия (результат и фактор), если 2 и более – множественная. По типу данных. А) простейшая модель(классическая нормальная линейная модель) Б) более сложная – модель с фиктивными переменными (хотя бы один из факторов является неколичественной переменной) В) Логит и пробит модели – это модели в которых результат является неколичественной переменной и может принимать два значения либо количественное с переменной значением 0;1, Г) Модели с цензурированными данными и тобит модели – это модели у которых на значение результата наложены ограничения не ниже, не выше. Д) модели временного ряда yt =a + bt + ε - модель Тренда t- номер момента времени y- показатель который меняется во времени, итд Вопрос №7. Понятие и показатели тесноты связи. К билету 7,8
Следовательно:
Опыт 1 Опыт 2. Опыт 3. Y^=a1+b1x Y^=a2+b2x Y^=a3+b3x R²1, b1>0 R²2, b2>0 b3<0
Если много экспериментов, то могут быть противоречивые результаты почти по всем коэффициентам регрессии приблизительно равным 0 в среднем. Если такой исход возможен, то говорят, что коэффициент регрессии незначителен. Параметр называется незначительным, если с большой долей вероятности его величина в генеральной совокупности = 0. Значимость уравнения регрессии –само уравнение регрессии – тождество чисел. Незначимость ур-я регрессии означает, что все параметры при факторах одновременно с высокой долей вероятности м.б. равны «0» в ген.сов-ти. Незначимость ур-я регрессии означает также незначимость коэф.детерминации, т.е его равенство «0» с высокой степенью вероятности в гень сов-ти. Значимость параметров -означает их отличие от 0 с высокой степенью вероятности, а параметра – все параметры при факторе одновременно не = 0. Для того, чтобы оценить значимость параметров и парного линейного коэффициента корреляции, используют критерий Стьюдента (t-критерий). Для оценки значимости ур-я регрессии в целом используется критерий Фишера.
В эконометрике все исходные данные рассматриваются как выборочные, значит, можно предположить, что при повторе статистического наблюдения полученные данные отличались бы друг от друга, а, значит, отличались бы и показатели по ним рассчитанные. Если много наблюдений, могут быть противоречивые результаты и коэффициент регрессии Значимость уравнения регрессии: Незначимость уравнения регрессии означает, что все параметры при факторах одновременно с высокой долей вероятности могут быть равны 0.
Незначимость уравнения регрессии, означает незначимость коэффициента детерминации, то есть его равенство 0 с высокой степенью вероятности в генеральной совокупности.
Уравнение значимо если все параметры при факторах одновременно не равны 0. Значимость уравнения говорит о том, что все факторы в уравнении оказывают влияние на результат. Для оценки значимости уравнения регрессии в целом используют критерий Фишера или F-критерий.
Критерий Стьюдента. Используется для оценки значимости параметров уравнения регрессии. Алгоритм оценки значимости по критерию Стьюдента: 1. Рассчитывается средняя ошибка оцениваемого параметра (или стандартная ошибка) - 2. 3. Фактическое значение t-критерия:, т.е. параметр делим на ошибку параметра 4. Сравнивается фактическое и табличное значение t-критерия, если tфакт> ИЛИ: 5. после пункта 2: Находим границы доверительного интервала для оценки параметра:
Этот доверительный интервал характеризует значения оцениваемого параметра, которые он может принимать в различных опытах с высокой долей вероятности. Длят того чтобы параметр был значим, необходимо,чтобы 0 не входил в доверительный интервал, если входит то говорим что параметр незначим в вероятностью 1-α, если не входит, то параметр значим с вероятностью 1-α. Формула средней ошибки параметра зависит от того какой параметр оценивается. Общая для всех параметров уравнения регрессии формула:
Где, i=0,1,2…p;
Стандартная ошибка регрессии: В большинстве случаев приведенную формулу можно упростить, если есть парное линейное уравнение регрессии, то ошибка рассчитывается в числителе SSост.
А для свободного члена Для множественной регрессии формула ошибки одного из коэффициентов регрессии:
R^2- коэффициент детерминации по всему уравнению
Общий критерий Фишера Значимость уравнения множественной регрессии в целом, так же как и в парной регрессии, оценивается с помощью F-критерия. Сопоставляя факторную и остаточную дисперсии в расчете на одну степень свободы, получим величину F-отношения, т.е. критерий F: F= Dфакт/Dост = (R²/1-R²) * (n-m-1/m), где Dфакт – факторная сумма квадратов на одну степень свободы R² - индекс (коэффициент) множественной детерминации n – число наблюдений m – число параметров при переменных x (в линейной регрессии совпадает с числом включенных в модель факторов) Dост – остаточная сумма квадратов на одну степень свободы. Величина m характеризует число степеней свободы для факторной суммы квадратов, а (n-m-1) – число степеней свободы для остаточной суммы квадратов. Применение критерия Фишера предполагает: 1) расчет фактического значения критерия Fфакт 2) по таблице – табличного значения Fтабл 3) сравнение Fфакт и Fтабл, если факт>табл, то оцениваемое уравнение регрессии значимо с вероятностью P= 1-a (альфа), где а- вероятность ошибки. Общий f-критерий:
SSост – остаточная сумма квадратов = Табличное значение F-критерия – это максимальная величина отношения дисперсий. Формулу фактического значения часто используют в измененном виде:
Таблица дисперсионного анализа Оценка значимости уравнения регрессии обычно дается в виде таблицы дисперсионного анализа.
19.Показатели частной корреляции и детерминации Для оценки изолирован влияния кажд фактора на рез-т при устранении воздействия прочих факторов модели исп-ся частные показатели корреляции. Показатели частн корреляц представляют собой отношение сокращения остаточной дисперсии за счет дополнит включения в анализ нов фактора к остаточн дисперсии, имевшей место до введения его в модель. 1)индекс частной корреляции для фактора х1. η yx1*x2x3…xn=корень из (G2yx2x3..xm(ост) – G2yx1x2x3..xm(ост))/G2yx2x3..xm(ост) Под корнем в числителе- сокращение остаточн дисперсии за счет включения в модель фактора x1 после остальных факторов. 2)частный коэф корреляции ryx1*x2x3..xm=корень из (1-(1– R2yx1*x2x3..xm)/(1- R2yx2x3..xm)) Рекурентные формулы расчета частн коэф корреляции 1го порядка: Порядок частн показателя корреляции соотв-ет числу факторных признаков, влияние котор устраняется. Для 2х факторн модели част коэф корреляции: ryx1*x2= (ryx1 - ryx2* rx1x2)/корень из((1- ryx22)* (1- rx1x22)) и ryx2*x1= (ryx2 - ryx1* rx1x2)/корень из((1- ryx12)* (1- rx1x22)) Измеряется от -1 до 1. Исп-ся для оценки целесообразности добавления нов фактора в ур-ние после других факторов. Если частн коэф корреляции стремится к 0, то добавление нов.фактора не целесообразно.
20. Частный F-критерий Для оценки статистич целесообразности добавления нов факторов в регрессион модель исп-ся частн критерий Фишера, т.к на рез-ты регрессион анализа влияет не только состав факторов, но и последовательность включения фактора в модель. Это обьясняется наличием связи между факторами. Fxj =((R2 по yx1x2...xm – R2 по yx1x2…xj-1,хj+1…xm)/(1- R2 по yx1x2...xm))*((n-m-1)/1) Fтабл (альфа,1, n-m-1) Fxj больше Fтабл – фактор xj целесообразно лючать в модель после др.факторов. Если рассматривается уравнение y=a+b1x1+b2+b3x3+e, то определяются последовательно F-критерий для уравнения с одним фактором х1, далее F- критерий для дополнительного включения в модель фактора х2, т. е. для перехода от однофакторного уравнения регрессии к двухфакторному, и, наконец, F-критерий для дополнительного включения в модель фактора х3, т.е. дается оценка значимости фактора х3 после включения в модель факторов x1 их2. В этом случае F-критерий для дополнительного включения фактора х2 после х1 является последовательным в отличие от F-критерия для дополнительного включения в модель фактора х3, который является частным F- критерием, ибо оценивает значимость фактора в предположении, что он включен в модель последним. С t-критерием Стьюдента связан именно частный F- критерий. Последовательный F-критерий может интересовать исследователя настадии формирования модели. Для уравнения y=a+b1x1+b2+b3x3+e оценка значимости коэффициентов регрессии Ь1,Ь2,,b3 предполагает расчет трех межфакторных коэффициентов детерминации.
Тест Парка Тест Парка – нахождение параметров для регрессии следующего вида: lnE^2=a+bln*xi+б, где xi - фактор, который предположительно оказывает влияние на дисперсионный остаток б - случайный остаток (но который остался от др. случ. остатка)
Оцен-ся значимость коэффициента b (знач, если t факт>t табл), если значимый – остатки гетероскедастичны, если незначим – гомоскед. Этот тест относится к тестам гетероскедастичности (для квадрата остатков). Предполагается, что дисперсия остатков связана со значениями факторов функции
Тест Глейзера |E| = а+bxi^k + б а,b – неизвестные параметры, зависят от ур. регрессии k – задается произвольно, обычно k может быть равно: -2;-1;-0,5;0,5;1;2. Дается оценка значимости b, если он значим – гетероскедостичность в остатке (т.е. отсутствие зависимости x от y) Если изменится форма регрессии, то параметры меняются. t>t табл -> параметры значимы -> гетероскедастичность по определенному фактору (xi). Если гетероскедостичность хотя бы по одному тесту -> остатки гетероскедостичны в общем и тест Глейзера можно не продолжать
Тест Уайта. используется для анализа гетероскедастичности случайных остатков (E). Т.е. изменения дисперсии случайных остатков от наблюдения к наблюдению. Для выбора хорошей модели уравнения регрессии необходимо, чтобы Е были гомоскедастичны, т.е. их дисперсия была постоянна, и не зависела от дисперсии фактора х. В тесте Уайта моделируется уравнение рессии,сост. из элементов, включающих все факторы, входящие в уравнение регрессии+Эти же факторы в квадрате+необязательная часть,- попарные произведения факторов. Для случая модели с двумя факторами (x1 и x2), ур-я будут иметь вид: E2=a+b11x1+b21x2+b12x12+b22x22+c12x1x2+δ В рамках теста нужно оценить знач-ть всего ур. в целом, с помощью F-критерия Фишера. Если Fфакт>Fтабл =>Ур. значимо => все ф-ры оказывают влияние на величину Е и => остатки гетероскед-ны. И наоборот. Из этого Ур-я иногда следует назвать факторы, вызыв-е гетероскед-ть остатков. Это ф-ры, имеющие значимые параметры при них. Находятся ф-ры с помощью t-критерия Стьюдента. Tсли Tфакт>Tтабл => ф-р значим и влияет на остатки, вызывая их гетероскедостичность, если же Tфакт<Tтабл, =>ф-р незначим и не влияет на остатки. Т.е. если Tтабл=2,45,а Tфакт по (x2)= - 4, можно сделать вывод, что x2 значим и влияет на гетероскедастичность остатков.(Т.К. значение t-критерия берём по модулю!)
Тест Гольдфельда-Квандта. С помощью этого теста исследуются случайные остатки (Е) на предмет гомоскедастичности. Этапы теста: 1. совок-ть наблюдений упорядочивают по фактору, кот. предположительно влияет на Е. 2. Всю эту совок-ть делят на три группы (n1,n2,n3). При этом, n1 и n3 должны содержать равное кол-во эл-тов(n1=n3). n2 мож.быть =n1 и n3 (Желательно!), или же быть меньше n1 и n3. 3. По 1 и 3 совок-ти строят ур-я регрессии используя Метод Наименьш.Квадратов. Причём они должны иметь ту же структуру, что и исходн. ур-е регр. Т.е. если исходн. ур-е имеет 2 фак-ра (x1,x2), то и новые ур-я должны иметь столько же фак-ров. 4. Для кажд.из 2-х ур-й рассчитывают остаточные дисперсии(соответственно SS1ост и SS3ост) 5. Далее находят фактич.знач-е F-критерия, для этого бОлшую остат.дисперсию делят на меньшую. (нпр. SS1ост /SS3ост) 6. Далее находят Fтабл при df1=df2=n1-m-1. Если Fфакт>=Fтабл, то остатки Е гетероскед-ны по тому фактору, по кот.мы проводили упорядоч-ние в 1п. Например: Отсортируем совок-ть по фактору x2(он предположит-но влияет на Е) Y x1 x2 121 56 28 80 114 36 56 124 42 75 98 46 88 102 50 45 17 54 110 116 54 63 28 56 113 50 63 160 115 88 203 118 105 237 154 106 Разделим совок-ть на 3 гр:n1=n3=n3=4 Построим Ур-я для n1 и n3 вида: y=a +b1x1+b2x2 +E y = 193 – 0,64x1 – 1,25x2 + E y = -17,8 + 0,49x1 + 1,57x2 + E SSост(1): = 57,1 SSост(3)= 503,3 Fфакт=503,3/57,1= 8,8 df1 = df2 = 4 -2-1 = 1, Fтабл=161,4 => Fфакт<Fтабл, значит х2 не значим, не влияет на остатки => E – гомоскед-ны
Вопрос 30 Применение МНК к одной из парных нелинейных функций регрессии (параболе, гиперболе, степенной, показательной) После того, как функции были приведены к линейной форме, с ними можно работать как с обычными линейными функциями. К линеаризованным функциям применяется МНК (для нахождения параметров уравнения регрессии) Применение MНК для оценки параметров параболы второй степени приводит к след системе нормальных уравнений: ∑y= n*a + b*∑x + c* ∑x^2 ∑y*x= a*∑x + b*∑x^2 + c*∑x^3 ∑y*x^2 = a*∑x^2 + b*∑x^3 + c* ∑x^4 Решить ее относительно параметров a, b и с можно методом определителей: a= ∆a/∆; b=∆b/∆; c=∆c/∆
Вопрос 31 Коэффициент эластичности для нелинейных функций. Э = f ‘ (x)* x / f (x) – общая формула. Потом коэф эласт рассчит для каждой конкретн функции через произв: Парабола (парабола второго порядка): Y=a + bx +cx^2 + E Y ‘ = b+2c, следовательно Э = ((b + 2*c*x) *x)/ (a+b*x+c*x^2) Как и в лин функции вместо x часто подставляют x средн. Для общей хар-ки эластичности, но это не ведет к упрощению. (Э ср. = b*x cр./ y ср.) Гипербола: Э = -b/ (a*x + b) Показательная: Э = x * ln b Степенная: F ‘ (x) = a*b*x^(b-1) соответственно Э = b
№ 35 – Прогнозирование по нелинейным по параметрам функциям регрессии (степенной, показательной) Особенности прогнозирования по нелинейным функциям заключается в том, что сначала точечный и интервальный прогноз оценивается по линеаризованной форме, а затем при необходимости значение прогноза пересчитывается для исходной формулы. Необходимость возникает, когда функции были нелинейными по параметрам и следовательно зависимая переменная у была преобразована (пролонгирована). y=a+b/x +E y=a+bx+E x(среднее)=1/x yпр+(-)t(табличное)*m(упр) y=ax^bE lny=lna+blnx+lnE Y=A+BX+E Y(выровненный), пролонгированный=5 y(выровненный), пролонгир=е^yпр=е^5 Y пролонгир.min=3 y пролонгир.min= е^3 Yпролонгир.max=7 y пролонгир.min=е^7
Элементы временного ряда Временной ряд – совокупность значений какого-либо показателя, рассчитанного для одной единицы совокупности или для всей совокупности в целом, взятые за несколько последних моментов или периодов времени. Уровень ряда – конкретное значение рассматриваемого показателя. Уровень ряда можно условно разложить на след. элементы: 1. тенденция Тt 2. закономерные колебания St 3. случайные колебания Et Связать эти эл-ты можно следующим образом: · Аддитивная модель (сложение) yt=Тt + St + Et · Мультипликативная (умножение) yt=Тt * St * Et · Смешанная yt=Тt * St + Et Свойства временного ряда yt = ўt + ε для всех t и σyt - постоянная величина – такой ряд называется стационарным Не стационарный ряд – ряд стационарный остатков: ε = 0 σ=Const Если в стационарном ряду выполняется условие: r yt yt-k = 0 для любых k, то такой ряд называется белый шум.
Показатели колеблемости. Показатели колеблемости – это показатели любой колеблимости: 1. среднее линейное отклонение от тренда (тренд –это функция, отражающая зависимость значения уровня ряда от номера момента времени, или это математич. Описание тенденции), к-е рассчитывается как
2. среднее квадратическое отклонение от тренда
3. коэффициент колеблемости
Коэффициент автокорреляции не значим, т.е. в ряду нет закономерной колеблемости
Косвенный МНК Этот метод используется, если система точно идентифицируема. Решение: - Необходимо построить ПФМ и для каждого уравнения ПФМ найти парам-ры с помощью МНК - После нахождения парам-ов ур-я стар-ся преобразовать таким образом, чтобы получить уравнение, имеющее ту же стру-ру, что и ур-е СФМ. Успешный рез-т этих преобр-й является решением.
Двухшаговый МНК Этот метод используется, если система сверхидентифицируема. - Необходимо построить ПФМ и для каждого уравнения ПФМ найти парам-ры с помощью МНК - Для каждого ур-я СФМ (исходной модели) выпол-ся след. действие: 1. Находят эндогенные перем-е, явл-ся в дан. уравнении факторами 2. Испол-я ПФМ, рассчит-т выровнен-е значения переменных, выявл-я в предыдущем пункте (yˆ) 3. К рассматр-му ур-ю СФМ прим. МНК, причем вместо наблюд-х фактич. знач- эндоген. перм-х факторов берут выровнен-е значен-я, рассчит. в предыдущем пункте.
Ошибка аппроксимации
Общая вариация
Факторная вариация
Остаточная вариация
СКО
Свободный член
Коэффициент регрессии
Дисперсия
Коэффициент эластичности
Индекс корреляции
оценка значимости коэффициента регрессии (для линейной однофакторной модели): - нулевая теория
- остаточная дисперсия на 1 степень свободы - t-статистика, t-критерий Стьюдента. - t <>
- доверительный интервал
оценка статистической значимости уравнения регрессии - нулевая теория H0: r2 = 0 (R2 = 0)- отсутствие связи между признаками H1: r2 = 0 (R2 = 0) - F-критерий Фишера
оценка статистической значимости коэффициента корреляции
оценка статистической значимости в множественной регрессии: Частный критерий Фишера
стандартизация:
Частное уравнение регрессии
Предмет эконометрики, её связь с другими науками Термин «эконометрика» возник в 20 веке и изучает количественные и качественные экономические взаимосвязи с помощью математических и статистических методов и моделей. Эконометрика- это наука, изучающая количественные закономерности экономических явлений и процессов, с помощью статистических методов и моделей. Эконометрика дает инструментарий для экономических измерений, а также методологию оценки параметров моделей микро и макроэкономики. Кроме того, эконометрика активно используется для прогнозирования экономических процессов как в масштабах экономики в целом, так и на уровне отдельных предприятий. Эконометрика входит в обширное семейство дисциплин, посвященных измерениям и применению статистических методов в различных областях науки и практики. К этому семейству относятся, в частности, биометрия, наукометрия, психометрия, хемометрия, квалиметрия. Особняком стоит социометрия — этот термин закрепился за статистическими методами анализа взаимоотношений в малых группах, то есть за небольшой частью такой дисциплины, как статистический анализ в социологии
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1242; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.019 с.) |

 Функция которая отражает зависимость выравненных значений результатов от значений фактора называется функцией регрессии, или эта функция отражает корреляционную связь между показателями.
Функция которая отражает зависимость выравненных значений результатов от значений фактора называется функцией регрессии, или эта функция отражает корреляционную связь между показателями.
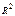 - обычно для множ регрессии, а если парная линейная регрессия, то
- обычно для множ регрессии, а если парная линейная регрессия, то Эта формула действует хороша только для парной регрессии.
Эта формула действует хороша только для парной регрессии. . Если r=0,72, то связь тесная (смотрим на модуль) минус показывает, что связь обратная.
. Если r=0,72, то связь тесная (смотрим на модуль) минус показывает, что связь обратная.




 0, если такой исход возможен, то говорят что коэффициент регрессии незначим.
0, если такой исход возможен, то говорят что коэффициент регрессии незначим.
 = >
= >  или
или 


 По таблице находят табличное значение t-критерия (при
По таблице находят табличное значение t-критерия (при  ); число степеней свободы = n-m-1, где n- число наблюдений, m- число факторов.
); число степеней свободы = n-m-1, где n- число наблюдений, m- число факторов.  - это число степеней свободы, на пересечении альфа и df находят t- табличное
- это число степеней свободы, на пересечении альфа и df находят t- табличное , то, говорят, что параметр значим с вероятностью 1-α, при этом tфактич. Берется по модулю!
, то, говорят, что параметр значим с вероятностью 1-α, при этом tфактич. Берется по модулю! , b- параметр
, b- параметр
 - диагональный элемент с N ii матрицы
- диагональный элемент с N ii матрицы  , причем i=0,1,2…p
, причем i=0,1,2…p



 - СКО
- СКО - коэффициент детерминации для уравнения регрессии в котором в качестве результатирующего признака входит xi, a в качестве признака остальные факторы входящие в уравнение регрессии.
- коэффициент детерминации для уравнения регрессии в котором в качестве результатирующего признака входит xi, a в качестве признака остальные факторы входящие в уравнение регрессии. =
= 
 - ошибка парного лин.коэф.корреляции
- ошибка парного лин.коэф.корреляции , где SSфакт – факторная сумма квадратов =
, где SSфакт – факторная сумма квадратов = 
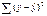 , n- кол-во наблюдений, m – кол-во параметров уравнения регрессии без свободного члена
, n- кол-во наблюдений, m – кол-во параметров уравнения регрессии без свободного члена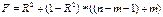
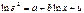 . Данная регрессия строится для каждого фактора в условиях многофакторной модели. Проверяется значимость коэффициента регрессии по критерию Стьюдента. Если коэффициент регрессии для уравнения
. Данная регрессия строится для каждого фактора в условиях многофакторной модели. Проверяется значимость коэффициента регрессии по критерию Стьюдента. Если коэффициент регрессии для уравнения  окажется статистически значимым, то существует зависимость
окажется статистически значимым, то существует зависимость 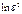 от lnx, то есть имеет место гетероскедастичность остатков.
от lnx, то есть имеет место гетероскедастичность остатков.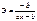
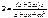
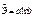


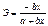

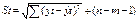



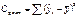




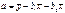

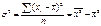



 H0:
H0: 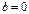 H1:
H1: 
 - определяется стандартная ошибка коэффициента регрессии
- определяется стандартная ошибка коэффициента регрессии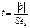
 ;
;  < t – гипотеза отклоняется, коэффициент значим.
< t – гипотеза отклоняется, коэффициент значим.

 - число степеней свободы для факторной дисперсии,
- число степеней свободы для факторной дисперсии,  - для остаточной.
- для остаточной.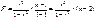

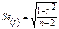
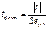
 используется при условии что
используется при условии что  а
а 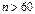 . В других случаях используется Z статистика.
. В других случаях используется Z статистика.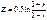

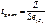


 - прирост степеней свободы (=1 при добавлении 1фактора)
- прирост степеней свободы (=1 при добавлении 1фактора) - натуральное уравнение
- натуральное уравнение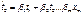 - стандартизированное уравнение (без свободного члена)
- стандартизированное уравнение (без свободного члена)




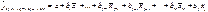 астный коэффициент эластичности
астный коэффициент эластичности