
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
По временной принадлежности данных.Содержание книги
Поиск на нашем сайте
А) пространственные данные – это данные взятые для разных единиц совокупности, в один и тот же момент времени. Б) модели с временными данными. Это данные взятые для одной совокупности в разные моменты времени. В) Модели с панельными данными. Модель для данных объединяющая предыдущие 2 типа. 4.Способы определения формы связей между показателями. Определение формы - это выбор конкретной математической функции которая описывает определенную связь. 1-й способ Графический Достоинство этого метода наглядность Недостаток – неточность. Можно найти конкретный результат(частный график), но невозможно построить общий график 2-й способ Теоретический (аналитический). Из предыдущих исследований известны сведения о форме функции. 3-й Экспериментальный.
Функциональная (детерминированная) зависимость – задается в виде формулы, которая каждому значению одной переменной ставит в соответствие строго определенное значение другой переменной(воздействием случайных факторов при этом принебрегают). Статистическая зависимость – это связь переменных на которую накладывается воздействие случайных факторов. При этом изменение одной переменной приводит к изменению математического ожидания – наиболее вероятного ожидаемого значения другой переменной. Уравнение регрессии – это формула статистической связи между переменными. Если эта формула линейна, она представляет собой линейную регрессию, а если нелинейная, то представляет собой нелинейную регрессию.
Общий вид модели линейной регрессии.
y = a + bx + ε - парная регрессия (частный случай)
p-количество факторов
В уравнении регрессии коэффициент при факторе называется коэффициентом регрессии. Во множественной регрессии иногда его называют коэффициент условно чистой регрессии. Матричная запись уравнения линейной регрессии.
Вектор параметров уравнения регрессии.
Вектор случайных остатков. Ε= Уравнение матричной формы. Y = XB + E
Сила связи характеризует, на сколько единиц в среднем изменится результат при изменении фактора на одну единицу. - прямая связь. Сила связи больше, где больше ∆y. ∆y Различают след. показатели силы связи: 1) Абсолютные пок -ли силы связи измеряются в тех же ед-х, что и изучаемые показ-ли. (руб,кг,шт..) 2) относительный показатель – коэф-т эластичности (изменение в среднем результата с изм-ем фактора на 1%). Это универсальный показатель силы связи, который рассчитывают для лин. и нелин. функций.
Например, для парной лин. регрессии y=a+bx+ ε Э=b*(x/ a+bx). Он не является постоянной величиной (изм-ся х). обычно для усредненной характеристики Э по линейной функции берут х среднее. 3) относит. показатель – стандартизированный коэф-т регрессии (рассчитывается только для множественной регрессии). Стандартизация: t = y-y‾/ сигма y. Так как для станд. переменных альфа а=0, то ур-ие регрессии в станд. масштабе примет вид: y=в1 * tх1 + …+вp * txp +e. в=L * сигма х/сигма y, где L-коэф-т при х в исходной множ. регрессии. При интерпретации коэф-та в ед. измерения – это сигма (ср. квадр. отклонение). Относит. Показатели силы применяются,чтобы сравнивать факторы по силе (обеспечить сопоставимость влияния показателей фактора на рез-т, чего не могут абсол. Показ-ли, т.к. изменения м.б несоизмеримыми) Можно сравнивать м\д собой коэф-т эластичности и стандартизир.показ-ли.
Вопрос №7. Понятие и показатели тесноты связи.
|
|||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 386; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.128.168.219 (0.01 с.) |

 Основной метод который предполагает расчет параметров разных функций(на основе наших исходных данных) и выборе из этих функций наилучшей по определенным критериям. Основной задачей экспериментального способа – это анаиз зависимости между переменными показателями. Значимость может быть функциональной или статистической.
Основной метод который предполагает расчет параметров разных функций(на основе наших исходных данных) и выборе из этих функций наилучшей по определенным критериям. Основной задачей экспериментального способа – это анаиз зависимости между переменными показателями. Значимость может быть функциональной или статистической. - это множественная регрессия(общий вид)
- это множественная регрессия(общий вид) y=
y=  x=
x= 
 b=
b= 

 6. Понятие и показатели силы связи в линейной регрессии
6. Понятие и показатели силы связи в линейной регрессии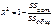 абсол. показатель – коэф-т регрессии (изменение результата при изм-ии фактора на 1 ед.). Он хар-ет также направление связи (если b>0, то связь прямая, если b<0, то обратная).
абсол. показатель – коэф-т регрессии (изменение результата при изм-ии фактора на 1 ед.). Он хар-ет также направление связи (если b>0, то связь прямая, если b<0, то обратная).




