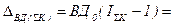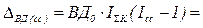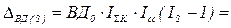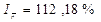Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Коэффициент роста и темп ростаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Темп прироста
Абсолютное значение 1 % прироста имеет смысл только для цепных характеристик динамических рядов:
Средние величины в рядах динамики: Средний абсолютный прирост
показывает абсолютное изменение показателя в среднем; Средний коэффициент роста, средний темп роста
показывают относительные изменения показателя в среднем за весь изучаемый период; Средний темп прироста
показывает на сколько процентов в среднем происходит изменение изучаемого показателя за весь период. Коэффициент опережения: позволяет сравнивать ряды динамики разного содержания. Средний уровень ряда динамики для интервальных рядов
для моментных рядов
Построение тренда в рядах динамики. линейный тренд: параболический тренд: где a - начальный уровень тренда в момент начала отсчёта t, b - среднегодовой абсолютный темп прирост, ускорение абсолютного изменения признака. Система нормальных уравнений для линейного тренда имеет вид:
Значения параметров а и b рассчитываются с использованием условных показателей времени, которые задаются самим исследователем. Оценка тренда производится на основе относительной ошибки тренда, величина которой должна быть близка к 6%. После оценки тренда можно осуществлять прогнозирование, подставляя вместо t значение, соответствующее прогнозируемому периоду. Пример решения и оформления типовой задачи: Имеются данные о днях трудопотерь вследствие нервных заболеваний на одном из предприятий. Таблица 9.1
1. Рассчитать характеристики ряда динамики, выполнить выводы об отдельных изменениях, построить графическое изображение относительных изменений изучаемых данных. 2. Определить общие закономерности изменений ряда, осуществить прогнозирование на основе рассчитанных показателей на 2004 г. 3. Построить аналитическое сглаживание на основе линейного тренда и осуществить прогноз на 2004 г. Решение:
2. 
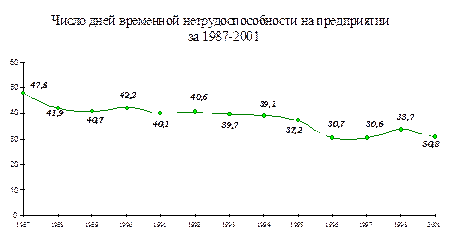
3. Рис.9.1 Графическое изображение числа болевших нервными заболеваниями на исследуемом предприятии
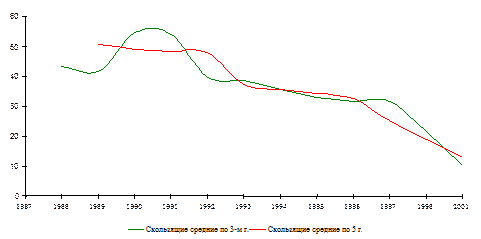
Рис.9.2 Графическое изображение скользящих средних по 3-м и 5-ти годам Так как графическое изображение исходных данных близко к прямой линии, что подтверждает и сглаживание на основе скользящих средних, то можно использовать для аналитического сглаживания уравнение линейного тренда: Контрольные вопросы: 1. Назовите абсолютные характеристики динамического ряда и формулы для их вычисления. 2. Назовите относительные характеристики динамического ряда и формулы для их вычисления. 3. Назовите средние характеристики интервального динамического ряда и формулы для их вычисления. 4. Назовите средние характеристики моментного динамического ряда и формулы для их вычисления. 5. Дайте понятие скользящей средней. 6. Дайте понятие тренда динамического ряда и их видов. 7. Какой тренд использовали в лабораторной работе.? 8. Дайте понятие коэффициента опережения, что он характеризует? 9. Как производится оценка данных, полученных на основе тренда? 10. Как осуществляется прогнозирование на основе тренда? Таблица 9.3
11. Сделайте выводы по выполненной работе. 12. Что называют рядом динамики и какие бывают виды динамических рядов? 13. Запишите систему нормальных уравнений для определения параметров линейного тренда. 14. Запишите систему нормальных уравнений для определения параметров параболического тренда. 15. Какой приём используют для упрощения расчётов параметров тренда в статистике? 16. Запишите формулу расчёта среднего квадратического отклонения теоретических от эмпирических значений уровней динамического ряда. Лабораторная работа № 10 Тема: «Расчёт экономических индексов в статистике». Компетенции: Студенты при выполнении данной лабораторной работы приобретают компетенции: - в области исследования конкретных процессов происходящих на хозяйствующих субъектах (производства или реализации); - в оценке изменений результирующих показателей, изменяющихся под влиянием соответствующих факторов в абсолютных и относительных величинах, для отдельного хозяйствующего субъекта; - в оценке изменений у разных хозяйствующих субъектов среднего значения качественного показателя в абсолютных и относительных величинах; - в построении уравнения аналитической зависимости показателя, характеризующего изменение явления во времени, и его использование для прогнозирования развития явления в будущем; - в проведении анализа на основе полученных результатов и выполнении выводов. Цель работы: Приобрести навык расчётов экономических индексов как агрегатных, так и средних из индивидуальных с использованием инструментария Microsoft Excel и проведения анализа на основе полученных результатов деятельности предприятия (продажи и производства). Краткая теория: Определение: В статистике под индексом понимают относительный показатель, который выражает соотношение величин какого-либо явления во времени, пространстве, сравнивает фактические данные с любым эталоном (нормативом, планом, прогнозом и т.д.) Основным элементом индексного соотношения является индексируемая величина. Основные обозначения и символы: p - цена (стоимость) единицы товара (продукции); q - количество (объём) какого-либо продукта (товара) в натуральном выражении; z - себестоимость единицы продукции; t - затраты времени на выработку единицы продукции; pq - стоимость продукции (товарооборот); zq - затраты (издержки) на производство продукции; tq - затраты времени (трудоёмкость) на производство продукции и т.д. индивидуальный индекс физического объёма- индивидуальный индекс цены - индивидуальный индекс себестоимости - индивидуальный индекс стоимости (товарооборота) - индивидуальный индекс издержек (затрат)- и т.д., где Определение: Общий индекс в статистике- относительный показатель, служащий для сравнения сложных явлений и включающий в себя индексируемую величину, состояния которой сравниваются и вес- показатель, определяющий значимость каждой индексируемой величины. Общие индексы строятся для количественных и качественных показателей. Кроме этого по способу расчёта показатели делятся на агрегатные индексы и средние из индивидуальных. Определение: Агрегатным индексом называется индекс, у которого числитель и знаменатель представляют собой набор непосредственно несоизмеримых и неподдающихся непосредственному суммированию элементов: сумму произведений двух величин, одна из которых меняется (индексируется), а другая (вес индекса)- остаётся неизменной в числителе и знаменателе, служит для соизмерения индексируемых величин. Типичным индексом количественного показателя является индекс физического объёма. Для вычисления этого индекса, являющегося сложным индексом, введём коэффициенты соизмерения, полученные умножением объёма каждого вида продукции (q) на соответствующую цену (p)- pq; себестоимость(z)- zq; затраты времени(t)- tq и т д. Тогда общий индекс физического объёма продукции (товара):
показывает, как изменилась стоимость в результате изменения объёма выпуска продукции (продаж);
показывает, как изменились издержки производства в результате изменения объёма выпуска продукции (продаж) и т.д. Общий индекс стоимости продукции (общий индекс товарооборота):
показывает, как изменилась стоимость продукции (товарооборот) в текущем периоде по сравнению с базисным. Для расчёта общего индекса как среднего из индивидуальных воспользуемся формулой (1), из которой получим значения недостающих элементов. Так, например, если по имеющейся информации нет значения
и т.д. Общие индексы средних величин. Изучение совместного действия факторов на изменение значения осредняемого признака и изменение структуры явления решается построением системы взаимосвязанных индексов: 1. Индекс переменного состава 2. Индекс постоянного состава 3. Индекс структурных сдвигов Пример решения и оформления задач: Задача 1 Данные о товарообороте в оптовых магазинах коммерческой фирмы. Таблица10.1
1. Произвести оценку выручки магазина № 1 всего и за счёт факторов в абсолютных и относительных величинах; 2. Произвести оценку средней цены на молоко всего и за счёт факторов в относительных и абсолютных величинах; 3. Сделать выводы по каждому пункту, сопровождая их рассчитанными показателями.
Решение: Таблица10.2
1. 2. Задача 2 Данные о затратах на производство сельскохозяйственной продукции Таблица 10.3
В хозяйстве № 1 себестоимость сои уменьшилась на 2%, картофеля увеличилась на 3% и молока увеличилась на 1,2%, в хозяйстве № 2 себестоимость сои осталась без изменения. 1. Произвести оценку изменения затрат в хозяйстве № 1 всего и с разложением по факторам в относительных и абсолютных величинах; 2. Произвести оценку изменения средней себестоимости на одноименную продукцию всего и с разложением по факторам в относительных и абсолютных величинах. Примечание: графу «Объем произведенной продукции» использовать для расчётов в п.2. Решение: 1. Таблица 10.4
Для расчётов в п.1 общего индекса себестоимости используется средний гармонический из индивидуальных, так как значений себестоимости единицы продукции в исходных данных нет.
2. Таблица 10.5
Контрольные вопросы: 1. Назовите индивидуальные индексы и формулы их расчёта, каков экономический смысл индивидуальных индексов? 2. Какие виды общих индексов знаете по способу расчёта? 3. Какие индексы называют общими индексами количественных показателей? 4. Какие индексы называют общими индексами качественных показателей? 5. Какая взаимосвязь существует между количественными и качественными индексами? 6. Каков экономический смысл общего индекса цены (себестоимости, трудозатрат, товарооборота, издержек производства, физического объёма)? 7. Каков экономический смысл разности между числителем и знаменателем общего индекса физического объёма (цены, себестоимости, стоимости реализованной продукции, издержек производства, трудозатрат)? 8. Назовите формулы для расчёта общего индекса стоимости проданной продукции (цены, объёма продаж, затрат на производство продукции, себестоимости) как агрегатного индекса. 9. Назовите формулы для расчёта общего индекса стоимости проданной продукции (цены, объёма продаж, затрат на производство продукции, себестоимости) как среднего арифметического из индивидуальных индексов. 10. Назовите формулы для расчёта общего индекса стоимости проданной продукции (цены, объёма продаж, затрат на производство продукции, себестоимости) как среднего гармонического из индивидуальных индексов. 11. Что такое индекс структурных сдвигов? 12. Что такое индекс переменного состава? 13. Какая существует взаимосвязанная система индексов, описывающая влияние факторов на изменение значений осредняемого признака? Опишите эту взаимосвязь формулой. Лабораторная работа №11 Тема: «Изучение показателей, характеризующих эффективность деятельности предприятия» Компетенции: Студенты при выполнении данной лабораторной работы приобретают компетенции: - в области исследования конкретных процессов происходящих на хозяйствующих субъектах производящих продукцию и оказывающих услуги; - в оценке изменений результирующих показателей эффективности или эффекта от деятельности отдельного хозяйствующего субъекта на основе взаимосвязей, выраженных произведением и суммированием (мультипликативных и аддитивных моделей); - в проведении анализа на основе полученных результатов и выполнении выводов. Цель работы: Получения навыков в построении мультипликативных и аддитивных моделей для анализа эффективности деятельности предприятий производящих продукцию и оказывающих услуги. Краткая теория: В условиях рыночной экономики важное значение имеет устойчивое финансовое состояние предприятия, которое характеризуется целой системой показателей, состоящей из четырёх групп (показатели ликвидности, оборачиваемости активов, привлечения средств и прибыльности). Прибыльность предприятия определяется показателями рентабельности продукции и предприятия. Рентабельность продукции рассчитывается:
а предприятия где Пр – прибыль, полученная от реализации продукции, С- затраты на её производство, Пб –прибыль предприятия, К - величина капитала. Анализируя показатели прибыльности и рентабельности предприятия, статистика характеризует и влияние на эти показатели отдельных факторов. Так относительные показатели изменения среднего уровня рентабельности определяются системой индексов:
с1,с0 - затраты на производство и реализацию продукции, d1,d0 – удельный вес затрат на производство и реализацию продукции в общих затратах. Тогда абсолютное изменение среднего уровня рентабельности в общем: За счёт факторов: · Рентабельности отдельных видов продукции
· Структуры
Статистика результатов деятельности коммерческого банка может быть проведена на основе расчёта валового дохода коммерческого банка и анализа влияния факторов на величину изменений этого результирующего показателя. Согласно стандартной классификации виды предоставления кредитов в зависимости от времени: ¨ Краткосрочный; ¨ Среднесрочный; ¨ Долгосрочный. Влияние факторов величины процентной ставки, а также средней задолженности, на валовой доход банка может быть описан следующими характеристиками: Индекс физического объёма кредитных услуг Индекс изменения величины кредитной ставки за кредит
При анализе структурных изменений вклад разных факторов в общий прирост можно определить следующей мультипликативной индексной моделью:
где Примеры решения и оформления задач Пример 1: Таблица 11.1Показатели кредитной деятельности коммерческого банка
1. Оценить изменение валового дохода коммерческого банка в абсолютных и относительных величинах всего и за счёт влияния двух факторов на основе мультипликативной и аддитивной моделей; 2. Оценить влияние трех факторов (изменение объёма задолженности, перераспределения по формам кредита, изменения процентной ставки за кредит) на основе мультипликативной модели в абсолютных величинах; 3. Сделать выводы по каждому пункту. Решение: 1. 2. Таблица 11. 2
Пример 2: Таблица 11.3 Данные о финансово-хозяйственной деятельности предприятия в базисном и отчетном периодах
По данным о деятельности предприятия определить: 1. Уровень рентабельности по каждому виду продукции и в целом по двум видам продукции за каждый период; 2. Общие индексы рентабельности (переменного, фиксированного составов и структурных сдвигов); 3. Абсолютное изменение средней рентабельности за счёт влияния рентабельности отдельного вида продукции и структурных сдвигов. 4. Сделать выводы по каждому пункту. Решение:
3) 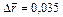 ; ;  ; ; 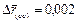 ; ;
Контрольные вопросы: 1. Какие индексы описывают изменения валового дохода коммерческого банка? 2. Какой показатель принят Вами за количественный, а какой - за качественный? 3. Какие факторы описывают изменение валового дохода в п.1 первой задачи? 4. Какие факторы описывают изменение валового дохода в п.2 первой задачи? 5. Что показывают абсолютные величины изменений валового дохода КБ в п.1 задачи? 6. Что показывают абсолютные величины изменений валового дохода КБ в п.2 задачи? 7. Какая мультипликативная модель использована для оценки во втором примере? 8. Какие факторы оказывают влияние на изменение изучаемого показателя? 9. Что показывают абсолютные величины изменения рентабельности? 10. Что показывают относительные величины изменения рентабельности? Лабораторная работа № 12.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1368; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.201.46 (0.01 с.) |

 ,
, 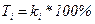 - темп роста (9.2)
- темп роста (9.2)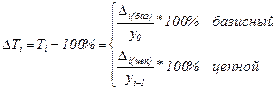 (9.3)
(9.3)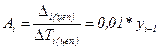 (9.4)
(9.4)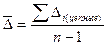 - (9.5)
- (9.5)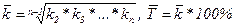 (9.6)
(9.6)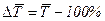 (9.7)
(9.7)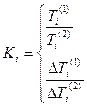 (9.8)
(9.8)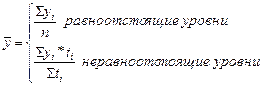 (9.9)
(9.9) (9.10)
(9.10) (9.11)
(9.11)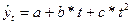 (9.12)
(9.12)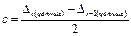 (9.13)
(9.13)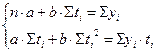 (9.14)
(9.14)
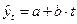 . Для расчёта параметров тренда построим таблицу 9.3, тогда
. Для расчёта параметров тренда построим таблицу 9.3, тогда 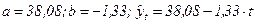 , для оценки тренда рассчитаем относительную ошибку d=5,38%. Тогда на основе тренда можно прогнозировать значение изучаемого показателя, причем t=8 и y2004=27,42 дней.
, для оценки тренда рассчитаем относительную ошибку d=5,38%. Тогда на основе тренда можно прогнозировать значение изучаемого показателя, причем t=8 и y2004=27,42 дней. ; (10.1)
; (10.1)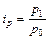 ; (10.2)
; (10.2)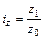 ; (10.3)
; (10.3)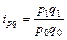 (10.4)
(10.4) (10.5)
(10.5)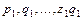 - значения соответствующего показателя в отчётном (текущем) периоде,
- значения соответствующего показателя в отчётном (текущем) периоде, 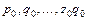 - значения этих показателей в базисном периоде.
- значения этих показателей в базисном периоде.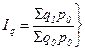 (10.6)
(10.6)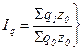 (10.7)
(10.7)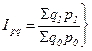 (10.8)
(10.8)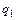 , а имеются значения
, а имеются значения 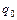 и
и 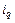 , то
, то 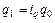 , и тогда:
, и тогда: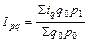 (10.9)
(10.9) ; (10.10)
; (10.10) ; (10.11)
; (10.11)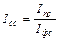 (10.12)
(10.12)

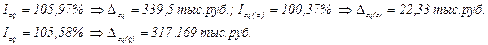
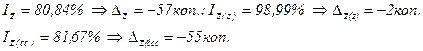
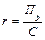 , (11.1)
, (11.1)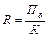 , (11.2)
, (11.2) , (11.3)
, (11.3)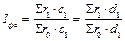 , (11.4)
, (11.4) (11.5)
(11.5)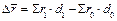 (11.6)
(11.6)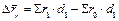 ; (11.7)
; (11.7) . (11.8)
. (11.8)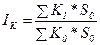 ; (11.9)
; (11.9)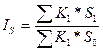 . (11.10)
. (11.10)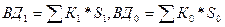 , где К1, К0 - средняя величина задолженности в отчётном и базисном периодах соответственно, S1, S0 - средняя процентная ставка, причём
, где К1, К0 - средняя величина задолженности в отчётном и базисном периодах соответственно, S1, S0 - средняя процентная ставка, причём 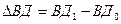 - общий прирост валового дохода и т.д.
- общий прирост валового дохода и т.д.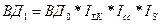 (11.11)
(11.11)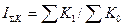 ,
, 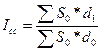 , причём последний индекс рассчитывается на основе удельных весов соответствующих видов кредита.
, причём последний индекс рассчитывается на основе удельных весов соответствующих видов кредита.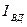 =127,322%;
=127,322%; 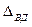 =1145,9945 тыс. руб.;
=1145,9945 тыс. руб.; 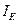 =122,2270%;
=122,2270%; 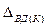 =932,27795 тыс. руб.;
=932,27795 тыс. руб.;  =104,1688%;
=104,1688%; 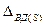 =213,7165186 тыс. руб..
=213,7165186 тыс. руб..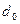
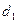
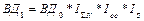
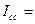 92,724%
92,724%