Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: «меры вариации. Оценка влияния фактора, положенного в основание группировки».Содержание книги
Поиск на нашем сайте
Компетенции: Студент в результате выполнения лабораторной работы приобретает компетенции: - в выборе фактора и результата для исходных данных - в расчёте различных мер вариации, необходимых для оценки влияния признаков друг на друга; - в оценке полученных результатов; - графической иллюстрации полученных результатов. Меры вариации позволяют оценить размеры вариации признака и их отличие от средней величины, оценить две характеристики масштабов и направления влияния признака, положенного в основание группировки – группировочного, оценить однородность совокупности исходных данных на основе специального показателя. Цель работы: Усвоить приемы расчёта размаха и средней величины отклонений вариационных рядов с использованием возможностей приложения Microsoft Excel 7.0, оценки вариации данных характеристик, однородности совокупности исходных данных, оценка влияния фактора на вариацию результативного признака. Краткая теория: Размах или колеблемость варьирующего признака - важный показатель ряда:
наиболее простой измеритель вариации признака, но размах не отражает изменения признака внутри интервала [ xmax; xmin ]. Характеристикой, которая дает обобщенную характеристику ряда и гасит случайные отклонения значений признака, является средняя. Вокруг значения средней величины происходят колебания признака, для обобщения этих колебаний применяется средняя величина этих отклонений. Для описания вариации и колеблемости признака вокруг средней величины в статистике применяются следующие величины: размах (колеблемость) признака, среднее линейное отклонение. При достаточно большом размахе величина линейного отклонения достигает или превышает среднее значение признака. При различии максимального и минимального значения признака на порядок или более, эта характеристика не описывает характер вариации и для такого описания применяют средний квадрат отклонений от средней величины или дисперсию и среднее квадратическое отклонение, которое является корнем второй степени из дисперсии. Среднее линейное отклонение (d) представляет собой среднюю арифметическую абсолютных значений отклонений отдельных значений признака (вариант) от их средней величины. СРЕДНЕЕ ЛИНЕЙНОЕ ОТКЛОНЕНИЕ ДЛЯ АРИФМЕТИЧЕСКОЙ ПРОСТОЙ: при исчислении средней величины по формуле простой средней арифметической СРЕДНЕЕ ЛИНЕЙНОЕ ОТКЛОНЕНИЕ ДЛЯ АРИФМЕТИЧЕСКОЙ ВЗВЕШЕННОЙ: при исчислении средней величины признака по формуле средней арифметической взвешенной. Дисперсия представляет собой средний квадрат отклонений отдельных значений признака (вариантов) от их средней величины. С дисперсией связана характеристика, называемая среднее квадратическое отклонение, которая показывает на сколько в среднем отклоняются конкретные значения признака (варианты) от их средней величины. СРЕДНЕЕ КВАДРАТИЧЕСКОЕ ОТКЛОНЕНИЕ ДЛЯ НЕ СГРУППИРОВАННЫХ ДАННЫХ:
средний квадрат отклонений от средней или дисперсия, которая описывает структуру совокупности.
среднее квадратическое отклонение от средней величины признака. СРЕДНЕЕ КВАДРАТИЧЕСКОЕ ОТКЛОНЕНИЕ ДЛЯ СГРУППИРОВАННЫХ ДАННЫХ:
дисперсия для сгруппированных данных.
среднее квадратическое отклонение от средней величины для сгруппированных данных. Такие характеристики вариации признака, как средняя величина и среднее квадратическое отклонение для интервальных рядов с равными интервалами могут быть рассчитаны по способу моментов: СРЕДНЕЕ ЗНАЧЕНИЕ ИЗУЧАЕМОГО ПРИЗНАКА ПО СПОСОБУ МОМЕНТОВ: СРЕДНИЙ КВАДРАТ ОТКЛОНЕНИЙ ПО СПОСОБУ МОМЕНТОВ: где А - условный нуль, равный варианте с максимальной частотой, h - шаг интервала, КОЭФФИЦИЕНТ ВАРИАЦИИ: Величина коэффициента вариации говорит об однородности изучаемой совокупности, так, если вариация меньше либо равняется 33%, то совокупность считается однородной. Для выполнения оценки влияния вариации фактора, положенного в основании группировки, на вариацию результативного признака (результата) используется правило сложения дисперсий, в котором отражена общая вариация под влиянием всех фактором на базе общей дисперсии: Систематическая вариация результата под влиянием признака-фактора, положенного в основание группировки оценивается на базе межгрупповой дисперсии: Вариация под влиянием неучтенных факторов оценивается на базе средней из внутригрупповых дисперсий: средняя из внутригрупповых: где Правило сложения дисперсий: Рассчитывается эмпирическое корреляционное отношение:
которое показывает по шкале Чеддока силу связи между фактором и результатом, знак перед корнем показывает направление связи. Таблица 6.1
Из таблицы 6.1 видно, что Пример решения и оформления типовой задачи: Данные о результатах сессии студентов одной из специальностей университета Таблица 6.2
1. Произвести сложную группировку по показателям «пол» и «средний балл»; 2. Оценить влияние фактора «пол» на средний балл сессии: силу и тесноту связи; 3. Оценить однородность совокупности; 4. Сделать выводы по результатам расчётов. Таблица 6.3
Для построения группировки используем функции: сортировки по «полу», затем по «среднему баллу», «СЧЁТ» и «СУММ». Дополним эту таблицу необходимыми графами для расчёта показателей вариации общей, межгрупповой и средней из внутригрупповых дисперсий, рассчитав предварительно средний балл по всей совокупности. Следует обратить внимание на то, что результат суммирования численности групп – 80 студентов. На основе выполненных расчётов можно сделать такие выводы: оценка за экзамен практически не зависит от того, кто сдаёт девушка или юноша (по шкале Чеддока эмпирическое корреляционное отношение менее 0,3) коэффициент детерминации демонстрирует, что только 7,2% оценок зависит от пола студента. Контрольные вопросы: 1. Какие формулы средних использованы для расчёта среднего балла в группе и по всей совокупности? 2. Какие ряды называют вариационными? 3. Какие меры вариации знаете для вариационных рядов, запишите их расчётные формулы? 4. Для каких рядов применяют формулы вычисления средней величины изучаемого признака и дисперсии по способу моментов, назовите формулу для вычисления средней величины по способу моментов, формулу для вычисления дисперсии по способу моментов. 5. Опишите алгоритм проведения группировки в лабораторной работе. 6. Опишите правило 3 7. Сделайте выводы по результатам выполненной работы.
Лабораторная работа № 7.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 397; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.146.176.112 (0.007 с.) |

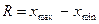 (6.1)
(6.1)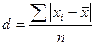 (6.2)
(6.2)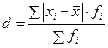 (6.3)
(6.3)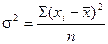 (6.4)
(6.4)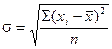 (6.5)
(6.5)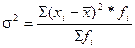 (6.6)
(6.6)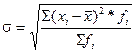 (6.7)
(6.7)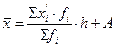 (6.8)
(6.8)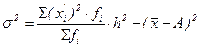 (6.9)
(6.9)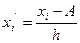 (6.10)
(6.10)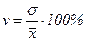 (6.11)
(6.11)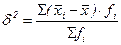 . (6.13)
. (6.13)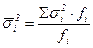 (6.14)
(6.14)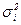 - внутригрупповая дисперсия показывает вариацию внутри группы и рассчитывается:
- внутригрупповая дисперсия показывает вариацию внутри группы и рассчитывается: 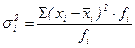 . (6.15)
. (6.15)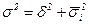 (6.16).
(6.16).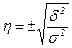 (6.17),
(6.17),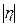
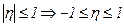 . Тесноту связи между признаками показывает эмпирический коэффициент детерминации
. Тесноту связи между признаками показывает эмпирический коэффициент детерминации 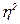 , выраженный в процентах.
, выраженный в процентах.