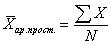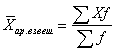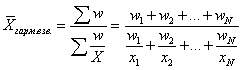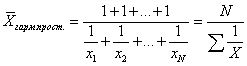Понятие и виды средних величин, их прикладное значение

Следующие обобщающие показатели после абсолютных и относительных данных – это средние величины и связанные с ними показатели вариации. Они имеют исключительное значение в экономическом анализе и играют важную роль в юридической статистике. Только с помощью средних можно охарактеризовать совокупности по количественному варьирующему признаку, по которому можно их сравнивать.

Предположим, нам необходимо сопоставить судебную практику назначения уголовных наказаний в двух районах, схожих по уровню и структуре преступности. Эту задачу нельзя решить на основе сравнения мер наказаний, назначенным конкретным осужденным, хотя какие-то суждения и можно высказать, если за одинаковые по квалификации деяния были назначены существенно различающиеся меры наказания. Нельзя этого сделать и на основе сопоставления большого количества данных о назначенных наказаниях. Но если мы сложим все сроки наказания (варианты, обозначив их символами дср х2, х3 и т. д.) и разделим на общее число осужденных (п), то по полученным средним данным можно сказать, какая практика назначения наказания в том и другом суде и сравнить ее на основе средних показателей. При обобщении наказаний, не связанных с лишением свободы, могут быть применены порядок, используемый при их сложении (ст. 71 УК РФ), и другие правила о которых говорилось при анализе индекса судимости.

В этом случае меры наказания, назначенные в том или ином суде, получают обобщенную характеристику в средних величинах, которые являются результатом абстрагирования от имеющихся индивидуальных различий, но с сохранением их основных свойств, в которых индивидуальные отклонения взаимопо-гашаются.

Таким образом, с помощью средних величин можно сравнивать интересующие нас совокупности юридически значимых явлений по тем или иным количественным признакам и делать из этих сравнений необходимые выводы не только о сроках наказания, но о возрасте правонарушителей (осужденных, заключенных), сроках расследования и рассмотрения уголовных и гражданских дел, о цене исков и т. д.

Средняя величина в статистике представляет собой обобщенную характеристику совокупности однородных явлений по какому-либо одному количественно варьирующему признаку. Она всегда обобщает количественную вариацию признака, к примеру, возраст правонарушителей от 14 до 60 лет, меры наказания от 1 месяца до 20 лет. Этот признак, хотя и в разной степени, но присущ всем единицам совокупности. Каждый правонарушитель имеет тот или иной возраст, а также каждый осужденный получил ту или иную меру наказания, измеряемого непосредственно в годах (баллах). Поэтому за всякой средней скрывается ряд распределения единиц совокупности по изучаемому признаку, т. е. вариационный ряд.

Средняя величина – это обобщающий показатель, который представляет собой типичную характеристику качественно однородных массовых процессов и явлений по какому-либо одному количественно-варьирующему признаку. Правовая статистика использует средние величины для характеристики: средних сроков рассмотрения УД, среднее число краж в месяц, средний размер ущерба, средний возраст осужденных лиц, средняя нагрузка судей и др.

Виды средних – это структурные средние и степенные средние

Первые это – мода и медиана. Вторые – средняя арифметическая, средняя гармоническая, средняя геометрическая, средняя квадратичная.

Вопрос 18. Степенные средние: средняя арифметическая, средняя гармоническая, средняя геометрическая.

Степенные средние могут быть простыми и взвешенными.

Простая средняя величина рассчитывается при наличии двух и более несгруппированных статистических величин, расположенных в произвольном порядке по следующей общей формуле:

Общая формула простой степенной средней величины

Взвешенная средняя величина рассчитывается по сгруппированным статистическим величинам с использованием следующей общей формулы:

Общая формула взвешенной степенной средней величины

где X – значения отдельных статистических величин или середин группировочных интервалов;

m - показатель степени, от значения которого зависят следующие виды степенных средних величин:

при m = -1 средняя гармоническая;

при m = 0 средняя геометрическая;

при m = 1 средняя арифметическая.

Средняя арифметическая.

Средняя арифметическая - это самая часто используемая средняя величина, которая получается, если подставить в общую формулу m=1. Средняя арифметическая простая имеет следующий вид:

где X - значения величин, для которых необходимо рассчитать среднее значение; N - общее количество значений X (число единиц в изучаемой совокупности).

Средняя арифметическая взвешенная имеет следующий вид:

где f - количество величин с одинаковым значением X (частота).

Если значения X заданы в виде интервалов, то для расчетов используют середины интервалов X, которые определяются как полусумма верхней и нижней границ интервала. А если у интервала X отсутствует нижняя или верхняя граница (открытый интервал), то для ее нахождения применяют размах (разность между верхней и нижней границей) соседнего интервала X.

Средняя гармоническая.

Средняя гармоническая применяется, когда исходные данные не содержат частот f по отдельным значениям X, а представлены как их произведение Xf. Обозначив Xf=w, выразим f=w/X, и, подставив эти обозначения в формулу средней арифметической взвешенной, получим формулу средней гармонической взвешенной:

Таким образом, средняя гармоническая взвешенная применяется тогда, когда неизвестны частоты f, а известно w=Xf. В тех случаях, когда все w=1, то есть индивидуальные значения X встречаются по 1 разу, применяется формула средней гармонической простой:

Средняя геометрическая.

Средняя геометрическая применяется при определении средних относительных изменений. Геометрическая средняя величина дает наиболее точный результат осреднения, если задача стоит в нахождении такого значения X, который был бы равноудален как от максимального, так и от минимального значения X.