
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Виды средней арифметической.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Наиболее часто в характеристике вариационного ряда используют среднюю арифметическую. Различают три вида средней арифметической: простая, взвешенная и вычисленная по способу моментов. Средняя арифметическая, которая рассчитана в вариационном ряду, где каждая варианта встречается только 1 раз называется средней арифметической простой (табл. 4). Ее определяют по формуле: M= где М – средняя арифметическая, V – варианта изучаемого признака, n–число наблюдений. Если в исследуемом ряду одна или несколько вариант повторяются несколько раз, то вычисляют среднюю арифметическую взвешенную (табл. 2), когда учитывается вес каждой варианты в зависимости от частоты ее встречаемости. Расчет такой средней проводят по формуле: M= где М – средняя арифметическая взвешенная; ∑ - знак суммы; V – варианты (числовые значения изучаемого признака); P – частота, с которой встречается одна и та же варианта признака, т.е. сумма вариант с данным значением признака; n – число наблюдений, т.е., сумма всех частот или общее число всех вариант (∑p). Таблица 4 Определение среднего пульса у студентов-мужчин перед экзаменом (Расчет простой средней арифметической)
Пример: при определений среднего пульса у студентов перед экзаменом следует сначала вычислить ∑ V* p, а затем среднюю величинуM = Нередко при большом числе наблюдений для вычисления средней арифметической взвешенной используют сгруппированный вариационный (или разбитый на равные интервалы) ряд. Такой вариационный ряд должен быть непрерывным, варианты, расположенные в определенном порядке (возрастания или убывания), следуют друг за другом. Таблица 5 Определение среднего пульса у студентов-мужчин перед экзаменом (Расчет взвешенной средней арифметической)
При группировке вариационного ряда следует учитывать, что интервал выбирает исследователь, величина интервала зависит от цели и задач исследования. Число групп в сгруппированном вариационном ряду определяют в зависимости от числа наблюдений.При числе наблюдений от 31 до 100 рекомендуется иметь 5-6 групп, от 101 до 300 - от 6 до 8 групп, от 300 до 1000 наблюдений можно использовать от 10 до 15 групп. Расчет интервала (i) проводится по формеле:i =
Vmax – максимальное значение варианты, Vmin – минимальное значение варианты. Расчет средней взвешенной в сгруппированном ряду (или интервальном ряду требует определения середины интервала, которую вычисляют как полусуммукрайных значений группы.(табл. 3). Расчет средней величины производят по формуле: M = Таблица 6 Определение среднего роста студентов-мужчин 20-22 лет (Расчет взвешенной средней арифметическойв сгруппированном ряду)
В случаях, когда варианты представлены большими числами (например, масса тела новорожденных в граммах) и имеется число наблюдений, выраженное сотнями или тысячами случаев, взвешенная средняя арифметическая может быть вычислена по способу моментов (табл. 7) по формуле: M = A + гдеA – условно взятая средняя величина (чаще всего в качестве условной средней берется Мо); ∑ - знак суммы; α – отклонение каждой варианты в интервалах от условной средней = p – частота (число раз, с которым встречается одна и та же варианта признака). αp – произведение отклонения (α) на частоту (p); n – число наблюдений, т.е. сумма всех частот или общее число всех вариант (∑p). i – величина интервала = Таким образом, средняя взвешенная вычисленная по способу моментов, составила 176,74 см., что практический совпало с расчетами средней обычным методом – 176,7 см.. Однако при вычислений средней по способу моментов используют простые цифры, вычисление менее громоздки, что значительно облегчает и ускоряет расчеты.
Средняя арифметическая (средняя взвешенная) имеет ряд свойств, которые используют в некоторых случаях для упрощения расчета средней и получения ориентировочной величины. 1. Средняя арифметическая занимает срединное положение в строго симметричном вариационном ряду (M = M0 = Me). 2. Средняя арифметическая имеет абстрактный характер и является обобщающей величиной, выявляющей закономерность. 3. Алгебраическая сумма отклонений всех вариант от средней равна нулю: ∑ (V - M) = 0. На этом свойстве основан расчет средней по способу моментов. Таблица 7 Определение среднего роста студентов-мужчин 20-22 лет (Методика расчета средней арифметической величины по способу моментов, i = 5)
|
||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 1201; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.50.254 (0.009 с.) |

 ,
, ,
, уд/мин.
уд/мин.
 = 76,9 уд/мин. (табл. 5).
= 76,9 уд/мин. (табл. 5). =76,9 уд/мин.
=76,9 уд/мин.
 ,
, =
=  =176,7см.(табл. 6).
=176,7см.(табл. 6). 162
162
 = 167
= 167
 = 172
= 172
 = 177
= 177
 = 182
= 182
 187
187
 =
= 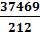 = 176,74 см.
= 176,74 см.







