
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Средними и относительными величинами.Содержание книги
Поиск на нашем сайте
Задача 1
Условие задачи: требуется определить, имеется ли достоверное снижение частоты пульса и приближение ее к норме в группе студентов после экзамена, если известно, что средняя частота пульса M1 до экзамена составила 98,8 удара в минуту (mM1= 4 удара в минуту); после экзамена (M2) – 84 в минуту (mM2 = 5 ударов в минуту).
Задание: требуется оценить достоверность разности между двумя средними величинами (M1 и M2)
Решение Достоверность разности между средними величинами определяется по формуле: t = Вывод. Поскольку t Задача 2 Условие задачи: при изучении успеваемости студентов медицинского института - не работающих и сочетающие учебу с работой - были получены следующие данные: у неработающих средний балл M1 = 4,1 (mM1 =
Задание: требуется оценить достоверность разности между двумя средними величинами (M1 и M2).
Решение Достоверность разности между средними величинами определяется по формуле: t = Вывод. Значение критерия t = 4,5 соответствует вероятности безошибочного прогноза P
Задача 3 Условие задачи: при медицинском осмотре детей 4 летнего возраста в 18 % (m = 3 %) случаях обнаружено нарушение опорно-двигательного аппарата (ОДА). Частота аналогичных нарушений ОДА при медосмотре детей 5 летнего возраста составила 24 % (m = 2,64 %).
Задание: оценить достоверность (существенность) различий в частоте нарушения ОДА у детей 2-х групп. t = Вывод. Значение критерия t = 1,5 соответствует вероятности безошибочного прогноза P
Задача 4 Условие задачи: При изучении эффективности иммунизации детей против гриппа получены следующие данные: процент заболевших в группе иммунизированных (P1) составил44,3 (m1 =
Задание: требуется оценить достоверность разности между двумя относительными величинами (P1 и P2). t =
Вывод. Значение критерия t = 1,5 соответствует вероятности безошибочного прогноза P Приложение 4 Задачи для самостоятельной работы Задание 1. СОСТАВЛЕНИЕ ПРСТОГО ВАРИАЦИОННОГО РЯДА И ВЫЧИСЛЕНИЕ ПРОСТОЙ СРЕДНЕЙ АРИФМЕТИЧЕСКОЙ (M) ПРИ МАЛОМ ЧИСЛЕ НАБЛЮДЕНИЙ На основе приведенных данных требуется: 1) составить простой вариационный ряд, 2) вычислить простую среднюю арифметическую (M). Вариант 1 Частота пульса (число ударов в минуту) у 12 лиц после проведение атропиновой пробы: 92, 84, 82, 100, 104, 96, 98, 102, 88, 80, 86, 106.
Вариант 2 У 10 матерей, имеющих пороки сердца, родились дети с массой тела (в кг.): 3,0, 3,2, 2,4, 2,6, 2,7, 2,0, 3,1, 2,8, 2,5, 2,2.
Вариант 3 Под наблюдением 9 участковых педиатров детской поликлиники состояло детей первого года жизни: 61, 54, 64, 62, 53, 60, 52, 56, 65.
Вариант 4 Результаты измерения температуры (в оC) у 7 новорожденных: 36,7, 37,1, 37,0, 37,2, 36,8, 36,9, 36,6.
Вариант 5 На 9 лекциях по общественному здоровью и здравоохранению в весеннем семестре на одном из потоков 4 курса присутствовала студентов: 120, 105, 110, 95, 98, 102, 96, 88, 90. Задание 2. СОСТАВЛЕНИЕ ПРОСТОГО ВАРИАЦИОННОГО РЯДА, ОПРЕДЕЛЕНИЕ МОДЫ И МЕДИАНЫ И ВЫЧИСЛЕНИЕ ВЗВЕШЕННОЙ СРЕДНЕЙ АРИФМЕТИЧЕСКОЙ (M) ПРИ БОЛЬШОМ ЧИСЛЕ НАБЛЮДЕНИЙ На основе приведенных данных требуется: 1) построить простой вариационный ряд, 2) найти моду (Mo) и медиану (Me), 3) вычислить взвешенную среднюю арифметическую (M). Вариант 1 Длительность нетрудоспособности (в днях) у 35 больных с острыми респираторными заболеваниями, лечившихся у участкового врача-терапевта: 6, 7, 5, 3, 9, 8, 7, 5, 6, 4, 9, 8, 7, 6, 6, 9, 6, 5, 10, 8, 7, 11, 13, 5, 6, 7, 12, 4, 3, 5, 2, 5, 6, 6, 7.
Вариант 2 Число состоящих на диспансерном учете больных у 33 невропатологов поликлиник крупного города: 85, 87, 90, 91, 89, 91, 90, 93, 94, 90, 93, 88, 98, 92, 94, 88, 96, 90, 92, 95, 87, 90, 91, 86, 92, 89, 97, 89, 99, 100, 82, 93, 88. Вариант 3
Частота дыхания (число дыхательных движений в минуту) у 47 мужчин в возрасте 40-45 лет: 12, 14, 13, 15, 16, 16, 16, 19, 19, 20, 20, 20, 19, 13, 15, 12, 15, 13, 15, 12 17, 12, 17, 16, 17, 13, 16, 17, 18, 14, 15, 16, 18, 14, 15, 14, 17, 18, 14, 18, 20 17, 18, 19, 20, 21, 22. Задание 3. СОСТАВЛЕНИЕ СГРУППИРОВАННОГО
|
||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 1224; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.247.57 (0.009 с.) |

 =
= 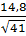 =
= 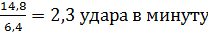 .
.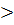 2,можно с вероятностью безошибочного прогноза больше 95 % утверждать, что после экзамена частота пульса у студентов снижается и приближается к норме.
2,можно с вероятностью безошибочного прогноза больше 95 % утверждать, что после экзамена частота пульса у студентов снижается и приближается к норме.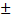 0,09), у сочетающих учебу с работой M2 = 3,65 (mM2 =
0,09), у сочетающих учебу с работой M2 = 3,65 (mM2 = 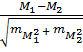 =
= 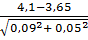 =
= 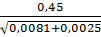 =
=  = 4,5.
= 4,5.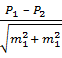 =
=  =
= 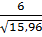 =
= 
 . Следовательно, различие в частоте нарушений ОДА детей, сравниваемых возрастных групп случайно, недостоверно, т.е. не обусловлено влиянием возраста детей.
. Следовательно, различие в частоте нарушений ОДА детей, сравниваемых возрастных групп случайно, недостоверно, т.е. не обусловлено влиянием возраста детей. в группе иммунизированных (P2) - 48,0 (m2 =
в группе иммунизированных (P2) - 48,0 (m2 = 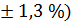 .
.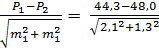 =
= 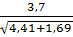 =
= 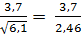 = 1,5
= 1,5


