
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
В отличие от статистических коэффициентов средние величиныСодержание книги
Поиск на нашем сайте Применяются для изучения а) вероятных признаков, которые могут быть или не быть б) постоянных признаков, присущих всем единицам наблюдения
Основное достоинство средних величин а) объективность, так как верно характеризуют свойство однородной совокупности б) типичность, так как указывают на характерную особенность данной совокупности в) абстрактность, так как отражают общее свойство данной совокупности г) конкретность, так как отражают признак, присущий данной совокупности
003. Модой называется варианта а) с наибольшей частотой б) с наименьшей частотой в) расположенная в центре ряда 004. Медианой называется варианта а) с наибольшей частотой б) с наименьшей частотой в) расположенная в центре ряда
Наиболее целесообразной формулой вычисления средней величины При малом числе наблюдений является а) б) в) С увеличением объема наблюдения ошибка репрезентативности а) увеличится б) останется без изменений в) уменьшится
Для вычисления ошибки для средних величин при малой выборке Используют формулу а) б) в) г)
008. Для вычисления ошибки для средних величин при большой выборке Используют формулу а) б) в) г)
Для вычисления ошибки для относительных величин используют формулу а) б) в) г)
010. Достоверность разности средних величин определяют по формуле a) б)
011. Достоверность разности относительных величин определяют по формуле a) б)
012. Критериями разнообразия признака являются а) лимит б) амплитуда в) среднее квадратичное отклонение г) коэффициент вариации д) все перечисленное верно
013. Размер ошибки средней арифметической величины зависит от: а) типа вариационного ряда б) числа наблюдений в) способа расчета средней величины г) разнообразия изучаемого признака
014. Для медико-социальных статистических исследований минимальной достаточной является вероятность безошибочного прогноза: а) 90 % б) 95% в) 99 %
015. При оценке достоверности разности полученных результатов исследования разность является достоверной (существенной), если при n tравна: а) 1,0 б) 1,5 в) 2,0 г) 3 и более
Приложение 3. ОБРАЗЕЦ ВЫПОЛНЕНИЯ ТИПОВОГО ЗАДАНИЯ Задание 1. СОСТАВЛЕНИЕ ПРОСТОГО ВАРИАЦИОННОГО РЯДА И ВЫЧИСЛЕНИЕ ПРОСТОЙ СРЕДНЕЙ АРИФМЕТИЧЕСКОЙ (M) ПРИ МАЛОМ ЧИСЛЕ НАБЛЮДЕНИЙ. Задача 1 Условие задачи: результаты измерения частоты дыхания (число дыхательных движений в минуту) у 8 мужчин в возрасте 35 лет: 20, 22, 18, 15, 16, 21, 24, 19.
Задание: на основе приведенных данных требуется: 1) составить простой вариационный ряд, 2) вычислить простую среднюю арифметическую (M).
Решение Поскольку в данном случае n Таблица 1 Частота дыхания (V)
Простую среднюю арифметическую определяем по формуле: M = Ответ: M = 19 дыхательных движений в минуту. Задача 2 Условие задачи: результаты измерения роста 10 мальчиков в возрасте 2 лет (в см.): 90, 92, 95, 91, 93, 96, 94, 98, 89, 97.
Задание:н а основе приведенных данных требуется: 1) составить простой вариационный ряд, 2) вычислить простую среднюю арифметическую (M). Решение Поскольку в данном случае n
Таблица 2 Результаты измерения роста
Простую среднюю арифметическую определяем по формуле: M = Ответ:M = 94 см. Задание 2. СОСТАВЛЕНИЕ ПРОСТОГО ВАРИАЦИОННОГО РЯДА, ОПРЕДЕЛЕНИЕ МОДЫ И МЕДИАНЫ И ВЫЧИСЛЕНИЕ ВЗВЕШЕННОЙ СРЕДНЕЙ АРИФМЕТИЧЕСКОЙ (M) ПРИ БОЛЬШОМ ЧИСЛЕ НАБЛЮДЕНИЙ Задача 1 Условие задачи: результаты лихорадочного периода при пневмонии у 32 больных (число дней): 3, 8, 14, 14, 7, 6, 4, 12, 13, 3, 4, 5, 10, 11, 5, 10, 10, 11, 12, 8, 9, 7, 7, 8, 9, 9, 7, 8, 12, 6, 10, 9.
Задание: на основе приведенных данных требуется: 1) построить простой вариационный ряд, 2) найти моду (Mo) и медиану(Me), 3) вычислить взвешенную среднюю арифметическую (M).
Решение 1. Строим простой (несгруппированный) вариационный ряд, последовательно располагая варианты в порядке возрастания с соответствующими им частотами (табл. 3): 2. Находим моду (Mo): с наибольшей частотой встречается варианта, равная 8 дням, следовательно, Mo = 8. Находим порядковый номер медианы (Me) по формуле 3. Вычисляем взвешенную среднюю арифметическую (M) по формуле: M = M = Ответ: M = 8,5 дня. Таблица 3
Задача 2 Условие задачи: получены следующие данные состоящих на диспансерном учете больных язвенной болезнью желудка и двенадцатиперстной кишки у 45 участковых терапевтов: 15, 16, 28, 17, 18, 19, 15, 27, 29, 21, 29, 27, 29, 22, 26, 25, 25, 25, 25, 26, 26, 22, 18, 17, 20, 21, 28, 30, 16, 15, 18, 19, 20, 20, 20, 20, 20, 21, 21, 22, 20, 22, 23, 23, 23.
Задание: на основе приведенных данных требуется: 1) построить простой вариационный ряд, 2) найти моду (Mo) и медиану(Me), 3) вычислить взвешенную среднюю арифметическую (M).
Решение 1. Строим простой (несгруппированный) вариационный ряд, последовательно располагая варианты в порядке возрастания с соответствующими им частотами (табл. 4): Таблица 4
2. Находим моду (Mo): с наибольшей частотой встречается варианта, равная 20 Д/б, следовательно, Mo = 20. Находим порядковый номер медианы (Me) по формуле 3. Вычисляем взвешенную среднюю арифметическую (M) по формуле:
M = = Ответ: M = 22 Д/б.
ЗАДАЧА 3
Условие задачи: получены следующие данные о длительности лечения в стационаре 45 больных пневмонией (в днях): 25, 11, 12, 13, 24, 23, 23, 24, 21, 22, 21, 23, 22, 21, 14, 14, 22, 20, 20, 15, 15, 16, 20, 20, 16, 16, 20, 17, 17, 19, 19, 19, 18, 18, 18, 18, 19, 19, 17, 17, 18, 18, 19, 26, 26. Задание: на основе приведенных данных требуется: 1) построить простой вариационный ряд, 2) найти моду (Mo) и медиану(Me), 3) вычислить взвешенную среднюю арифметическую (M). 4) составить сгруппированный вариационный ряд; 5) вычислить среднюю арифметическую (M) по способу моментов; 6) определить среднее квадратическое отклонение.
Решение 1. Строим простой (несгруппированный) вариационный ряд, последовательно располагая варианты в порядке возрастания с соответствующими им частотами (табл. 5): 2. Находим моду (Mo): с наибольшей частотой встречается варианта, равная 18 дням, следовательно, Mo = 18. Находим порядковый номер медианы (Me) по формуле 3. Вычисляем взвешенную среднюю арифметическую (M) по формуле:
M =
=
Ответ: M =.19 дней. Таблица 5
4. Пользуясь предыдущими данными составляем сгруппированный вариационный ряд (табл. 6); 1) определяем размах ряда вычитанием минимальной варианты из максимальной, Vmax. –Vmin. 2) определяем число групп (поскольку n = 45, число групп берем равным 6 – (табл. 6); 3) находим интервал (i) по формуле:
i =
4) начиная с минимальной варианты, строят вариационный ряд. Границы интервалов должны быть четкие, исключающие попадание одной и той же варианты в разные группы.
Таблица 6
5) определяем границы и середину каждой группы: например, первая группа вариант при i = 3 будет 11-13 дней, середина группы – 12 дней, следующая – 14-16 дней, середина 15 дней и т.д.; 6) распределяем изучаемую совокупность по группам, указывая им соответствующие частоты (p); 5. Вычисляем среднюю арифметическую (M) по способу моментов по формуле; M = A+ Порядок вычисления представлен в таблице 7 (за условную среднюю принимаем Mo = 18 дням,i = 3). Подставляем полученные значения в формулу: M = A + Ответ: M = 19,1 дня. (средняя взвешенная вычисленная по способу моментов (19,1 дня), совпало с расчетами средней обычным методом (19 дней). 5. Среднее квадратическое отклонение
σ = i Таблица 7
При этом первый момент средней нам известен (формула 5), он равен 1,1,
Для определение второго момента средней ( Получаем, что Ответ: σ = 3,63 дня. Задание 3
ОПРЕДЕЛЕНИЕ ОШИБКИ (mM) И ДОВЕРИТЕЛЬНЫХ ГРАНИЦ СРЕДНЕЙ ПРИ МАЛОМ ЧИСЛЕ НАБЛЮДЕНИЙ Задача 1 Условие задачи: результаты измерения частоты дыхания (число дыхательных движений в минуту) у 8 мужчин в возрасте 35 лет: 20, 22, 18, 15, 16, 21, 24, 19. Задание: на основе приведенных данных требуется: 1) составить простой вариационный ряд, 2) вычислитьпростую среднюю арифметическую (M), 3) определить среднееквадратическоеотклонение (σ), 4) вычислить ошибку (mM), 6) определить доверительные границы средней (M) при P = 95 % и P = 99 %.
Решение
1. Поскольку в данном случае n Таблица 1 Частота дыхания (V)
2. Простую среднюю арифметическую определяем по формуле: M = Ответ: M = 19 дыхательных движений в минуту. 3. Среднее квадратическое отклонение (σ) при n
σ =
определяем σ (табл. 2): Таблица 2 Частота дыхания (V)
Заносим данные таблицы в формулу: σ = 4. Ошибка средней определяется по следующей формуле: mM= 5. Доверительный интервал (tm = △) средней величины (M) определяем путем нахождения доверительного коэффициента t по таблице Стьюдента (табл. 8): а) при P = 95 % и при n = 8 t = 2,3; следовательно tm (△) = 2,3 ∙ 1,1 = 2,5 дых.движ. в мин., M = 19
Задание 4.ОПРЕДЕЛЕНИЕ ДОСТОВЕРНОСТИ РАЗНОСТИ МЕЖДУ
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 1887; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |






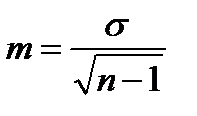

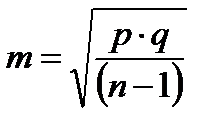


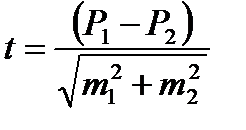

 30 величина
30 величина 30, а каждая варианта встречается один раз, строим простой вариационный ряд, располагая варианты в ранговом порядке (в порядке возрастания или убывания) (табл. 1):
30, а каждая варианта встречается один раз, строим простой вариационный ряд, располагая варианты в ранговом порядке (в порядке возрастания или убывания) (табл. 1): = 19 дыхательных движений в минуту. (1)
= 19 дыхательных движений в минуту. (1)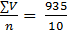 = 94см. (2)
= 94см. (2) =
= 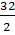 = 16, следовательно, 16-я по счету варианта является медианой. В нашем примере такой вариантой является 10, т.е, Me = 10 дням, Mo = 8 дням.
= 16, следовательно, 16-я по счету варианта является медианой. В нашем примере такой вариантой является 10, т.е, Me = 10 дням, Mo = 8 дням. (3)
(3)
 =
=  = 23, следовательно, 23-я по счету варианта является медианой. В нашем примере такой вариантой является 18, т.е, Me = 18 Д/б, Mo = 20Д/б.
= 23, следовательно, 23-я по счету варианта является медианой. В нашем примере такой вариантой является 18, т.е, Me = 18 Д/б, Mo = 20Д/б.
 Д/больных.
Д/больных.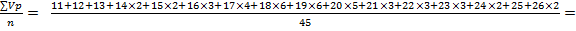
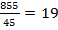 дней.
дней. =
= 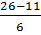 =
=  = 2,5
= 2,5 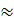 3; (4)
3; (4) ; (5)
; (5) = 18 +
= 18 + 
 в данном случае определяем по способу моментов по формуле (пользуемся предыдущими данными)
в данном случае определяем по способу моментов по формуле (пользуемся предыдущими данными) . (6)
. (6)
 = (1,1)2 = 1,21.
= (1,1)2 = 1,21. i2) необходимо заполнить построчно графу α2pв табл. 7; ∑ α2p = 72.
i2) необходимо заполнить построчно графу α2pв табл. 7; ∑ α2p = 72. = 1,6 * 9 = 14,4, подставляем полученные данные в формулу (6) и получаемσ =
= 1,6 * 9 = 14,4, подставляем полученные данные в формулу (6) и получаемσ =  =
=  = 3,63 дня.
= 3,63 дня. 30, а каждая варианта встречается один раз, строим простой вариационный ряд, располагая варианты в ранговом порядке (в порядке возрастания или убывания) (табл. 1):
30, а каждая варианта встречается один раз, строим простой вариационный ряд, располагая варианты в ранговом порядке (в порядке возрастания или убывания) (табл. 1):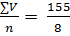 = 19 дыхательных движений в минуту. (1)
= 19 дыхательных движений в минуту. (1)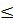 30 определяем по формуле:
30 определяем по формуле: , где d = V – M,
, где d = V – M, =
=  = 2,8 дых.движ. в мин.
= 2,8 дых.движ. в мин.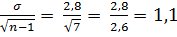 дых. движ. в мин.
дых. движ. в мин. 2,5 дых. движ. в мин, т. е. в генеральной совокупности при P = 95 % средняя величина числа дыхательных движений колеблется от 16,5 до 21,5 дых. движ. в мин.; при P = 99 % t = 3,3, tm (△) = 3,3 ∙ 1,1 = 3,6 дых. движ. в мин.; M = 19
2,5 дых. движ. в мин, т. е. в генеральной совокупности при P = 95 % средняя величина числа дыхательных движений колеблется от 16,5 до 21,5 дых. движ. в мин.; при P = 99 % t = 3,3, tm (△) = 3,3 ∙ 1,1 = 3,6 дых. движ. в мин.; M = 19 


