
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кафедра общественного здоровья и здравоохраненияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
КАФЕДРА ОБЩЕСТВЕННОГО ЗДОРОВЬЯ И ЗДРАВООХРАНЕНИЯ З.А. Бадоева УЧЕБНО-МЕТОДИЧЕСКОЕ ПОСОБИЕ ПОМЕДИЦИНСКОЙ СТАТИСТИКЕ (ВАРИАЦИОННЫЙ РЯД, СРЕДНИЕ ВЕЛИЧИНЫ, ОЦЕНКА ДОСТОВЕРНОСТИ РЕЗУЛЬТАТОВ ИССЛЕДОВАНИЯ,)
Владикавказ 2012 Составитель: И.о. заведующего кафедрой общественного здоровья и здравоохранения ГБОУ ВПО СОГМА Минздравсоцразвития России к.м.н., З.А. Бадоева;
Рецензенты: А.Р. Кусова – доктор мед.наук, профессор, зав. кафедрой общей гигиены ГБОУ ВПО СОГМА Минздравсоцразвития России
И.Ф. Боциев - канд. техн. наук, доцент, зав. кафедрой медицинской и биологической физики ГБОУ ВПО СОГМА Минздравсоцразвития России.
Учебно-методическое пособие предназначается для подготовки к практическим занятиям, аудиторной и внеаудиторной самостоятельной работе студентов медицинских вузов. В пособии представлены методы статистического анализа, широко применяемые как при изучении показателей здоровья на индивидуальном, групповом и популяционном уровнях, так и при анализе деятельности учреждений, системы охраны, укрепления и восстановления здоровья населения. Учебно-методическое пособие составлено в соответствии с учебной программой,
Утверждена ЦУКМС ГБОУ ВПО СОГМА Минздравсоцразвития России. Протокол № от 2012 г. ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ............................................................................................................................ 4 Глава1. ВАРИАЦИОННЫЙ РЯД И СРЕДНИЕ ВЕЛИЧИНЫ........................................ 5 1.1. Вариационный ряд. Построение вариационного ряда............................................ 5 1.2. Формы вариационного ряда.......................................................................................... 6 1.3. Этапы составления сгруппированного ряда............................................................... 8 1.4 Средние величины. Виды средних величин.............................................................. 12 1.5. Виды средней арифметической........................................................................... 14 1.6. Характеристика разнообразия признаков в совокупности....................................... 19 1.7. Коэффициент вариации........................................................................................ 24 Глава 3. ОЦЕНКА ДОСТОВЕРНОСТИ РЕЗУЛЬТАТОВ ИССЛЕДОВАНИЯ............ 26 2.1.Достоверность. Критерии понятия достоверности.................................................... 26 2..2. Определение средней ошибки средней (или относительной) величины (ошибки репрезентативности) – m................................................... 27 2.3. Определение доверительных границ M и P............................................................... 28 2.4. Определение достоверности разности средних(M) или относительных (P) величин (по критерию t)............................................................................................... 30 2.5. Оценка достоверности различия сравниваемых групп по критерию соответствия (хи-квадрат).................................................................................. 31 ПРИЛОЖЕНИЕ(контрольные вопросы, вопросы тестового контроля, типовое задание, задачи для самостоятельной работы, эталон ответов........................................ 33 ЛИТЕРАТУА (основная, дополнительная)....................................................................... 58
ВВЕДЕНИЕ Одним из важнейших элементов исследований является проведение научного анализа полученных данных на основе использования статистических методов. Изучение статистических методов способствует развитию у студентов и врачей критических взглядов, дедуктивных и индуктивных способностей (дедукция – метод анализа, при котором из общих положений логический выводятся частные; индукция – метод анализа от частного к общему). Статистический анализ позволяет обосновать ту или иную тактику врача в предупреждении и лечении заболеваний. В современном здравоохранении статистические методы используются на всех уровнях отрасли: от работы участкового врача, регистратуры поликлиники и до министерства, до научных учреждений. В связи с этим преподавание статистических методов в той или иной степени осуществляется на всех клинических кафедрах, а также более углубленно на кафедрах гигиены, здравоохранения, эпидемиологии и на этапах послевузовского образования. Анализ данных о заболеваемости и деятельности медицинских учреждений обычно включает относительно простые методы, которые в практике преподавания на кафедрах социальной медицины и общественного здоровья называют методами медико-статистических исследований. Учитывая, что врачи, как правило, проводят исследования на выборочных совокупностях, теория статистики позволяет с помощью математического аппарата (формул) переносить данные с выборочного исследования на генеральную совокупность. При этом врач должен уметь не только воспользоваться математической формулой, но сделать вывод, соответствующий каждому способу оценки достоверности полученных данных. С этой целью врач должен знать способы оценки достоверности. Таким образом, каждый врач должен уметь правильно использовать статистические методы и оценивать информацию, накопленную в различных областях его деятельности. Глава 2 ВАРИАЦИОННЫЙ РЯД И СРЕДНИЕ ВЕЛИЧИНЫ. Вариационный ряд. Построение вариационного ряда. Характер распределения изучаемых явлений, как правило, выявляют при анализе вариационных рядов, которые в силу этого носят еще название рядов распределения. Результаты многих клинических, лабораторных и других исследований, представленные в количественном выражений, часто многочисленны и вместе с тем малодоступны для общего их обозрения. В силу этого без соответствующей обработки они не пригодны для анализа. Необходимо получить обобщенные характеристики в виде средних величин и различных критериев разнообразия. Методику построения вариационного ряда рассмотрим на следующем примере. При измерении времени задержки дыхания у 50 женщин в возрасте 30-45 лет, приступивших к занятиям по общефизической подготовке, получены следующие данные (табл. 1). Таблица 1 Результаты измерения задержки дыхания после вдоха у 50 женщин в возрасте 30-45 лет (в секундах). Материалы, приведенные в таблице 1 не могут быть проанализированы без предварительной обработки и систематизации, что позволит сделать их удобными для анализа, доступными для вычисления показателей. Следовательно из этих данных надо построить вариационный ряд. Вариационный ряд – это ряд числовых измерений определенного признака, отличающихся друг от друга по своей величине расположенных в определенном порядке. Вариационный ряд состоит из вариант (V) и соответствующих им частот (p). Вариантой (V) называют каждое числовое значение изучаемого признака. Частота (p) - абсолютная численность отдельных вариант в совокупности, указывающая, сколько раз встречается данная варианта в вариационном ряду. Общее число случаев наблюдений, из которых вариационный ряд состоит, обозначают буквой (n). Построить вариационный ряд – значит упорядочить количественное распределение единиц совокупности по значениям признака, а затем подсчитать числа единиц совокупности с этими значениями (построить групповую таблицу). Ряд вариант одного и того же признака, расположенных в определенном порядке (по степени возрастания или убывания), с соответствующими им частотами, образуют вариационный ряд (пример: распределение новорожденных по весу, призывников по росту, и т.п.).
Формы вариационного ряда Выделяют три формы вариационного ряда: ранжированный ряд, дискретный ряд и интервальный ряд. Ранжированный ряд – это распределение отдельных единиц совокупности в порядке возрастания или убывания исследуемого признака. Ранжирование позволяет легко разделить количественные данные по группам, сразу обнаружить наименьшее и наибольшее значения признака, выделить значения, которые чаще всего повторяются. По характеру вариации различают дискретные (прерывные) и непрерывные признаки. Дискретный ряд – это такой вариационный ряд, в основу построения которого положены признаки с прерывным изменением (дискретные признаки). К последним можно отнести тарифный разряд, количество детей в семье, число работников на предприятии и т.д. Эти признаки могут принимать только конечное число определенных значений. Дискретный вариационный ряд представляет таблицу, которая состоит из двух граф. В первой графе указывается конкретное значение признака, а во второй – число единиц совокупности с определенным значением признака. Если признак имеет непрерывное изменение (размер дохода, стаж работы, стоимость основных фондов предприятия и т.д., которые в определенных границах могут принимать любые значения), то для этого признака нужно строить интервальный вариационный ряд. Групповая таблица здесь также имеет две графы. В первой указывается значение признака в интервале «от - до» (варианты), во второй – число единиц, входящих в интервал (частота). Вариационные ряды бывают простые или несгруппированные, которые составляют, как правило, при малом числе наблюдений (до 30 единиц наблюдения), и сгруппированные, которые составляют при большом числе наблюдений (более 30 единиц наблюдения). Если исследователь имеет не более 30 наблюдений, то достаточно все значения признака расположить в нарастающем или в убывающем порядке (от максимальной варианты до минимальной или наоборот) и указать частоту каждой варианты. При большом числе наблюдений (более 30) вариационный ряд рекомендуется сгруппировать. Для выбора количества групп в вариационном ряду необходимо учитывать число наблюдений, а также разность между максимальным и минимальным значениями вариант. При числе наблюдений от 31 до 100 рекомендуется иметь 5-6 групп, от 101 до 300 - от 6 до 8 групп, от 300 до 1000 наблюдений можно использовать от 10 до 15 групп (табл. 2). Таблица 2 Рис. 1. Этапы построения сгруппированного вариационного ряда. I этап: определение количества групп в вариационном ряду. При большом количестве групп ряд получается громоздким, что ведет к трудностям вычисления показателей. При малом числе групп в ряду интервал велик. Это приводит к крайне нежелательному снижению точности характеристик ряда, рассчитываемых на следующем этапе работы. При большом колебаний признака его максимальные величины могут не соответствовать размерам последней группы и будут вне ее. В этом случае необходимо увеличить число групп с тем, чтобы можно было включить эти крайние варианты. II этап: определение величины интервала (i) между группами. Определяя величину интервала между группами, амплитуду вариационного ряда (разность между максимальным и минимальным значениями вариант) делят на число групп (см. табл.1) n = 50 и тогда r = 10. Величина интервала i = Полученный интервал округляется до целого числа – 5. III этап: определение начала, середины и конца группы. Прежде всего, необходимо определить середину для первой группы. В нашем примере максимальная варианта равна 64. Поскольку середина группы должна делиться на величину интервала, то за середину первой группы следует взять варианту, равную 65, которая будет ближайшей к максимальному значению и без остатка разделится на величину интервала, равного 5. Середины для других групп находят следующим образом: от середины каждой предыдущей группы отнимают величину интервала. Так, если середина первой группы – 65, то середина второй группы равна 60 (65-5), середина третьей группы – 55 (60-5) и т. д. (табл. 3).После составления ряда из величин, принятых за середину группы – 65, 60, 55, 50 и т.д., нужно определить границы (начало и конец) этих групп. При этом следует иметь в виду, что границы не должны повторяться, иначе трудно будет распределить варианты по группам и построить вариационный ряд. Определяя начало группы, к ее середине прибавляют величину Границы должны составленный так, чтобы значения вариант не оказывались между группами, нежелательны также открытые группы. Например, «свыше 60» или «менее 20» и т. д. Таблица 3 Рис. 2. Графическое изображение вариационного ряда. Таблица 4 Определение среднего пульса у студентов-мужчин перед экзаменом (Расчет простой средней арифметической)
Пример: при определений среднего пульса у студентов перед экзаменом следует сначала вычислить ∑ V* p, а затем среднюю величинуM = Нередко при большом числе наблюдений для вычисления средней арифметической взвешенной используют сгруппированный вариационный (или разбитый на равные интервалы) ряд. Такой вариационный ряд должен быть непрерывным, варианты, расположенные в определенном порядке (возрастания или убывания), следуют друг за другом. Таблица 5 Определение среднего пульса у студентов-мужчин перед экзаменом (Расчет взвешенной средней арифметической)
При группировке вариационного ряда следует учитывать, что интервал выбирает исследователь, величина интервала зависит от цели и задач исследования. Число групп в сгруппированном вариационном ряду определяют в зависимости от числа наблюдений.При числе наблюдений от 31 до 100 рекомендуется иметь 5-6 групп, от 101 до 300 - от 6 до 8 групп, от 300 до 1000 наблюдений можно использовать от 10 до 15 групп. Расчет интервала (i) проводится по формеле:i = Vmax – максимальное значение варианты, Vmin – минимальное значение варианты. Расчет средней взвешенной в сгруппированном ряду (или интервальном ряду требует определения середины интервала, которую вычисляют как полусуммукрайных значений группы.(табл. 3). Расчет средней величины производят по формуле: M = Таблица 6 Определение среднего роста студентов-мужчин 20-22 лет (Расчет взвешенной средней арифметическойв сгруппированном ряду)
В случаях, когда варианты представлены большими числами (например, масса тела новорожденных в граммах) и имеется число наблюдений, выраженное сотнями или тысячами случаев, взвешенная средняя арифметическая может быть вычислена по способу моментов (табл. 7) по формуле: M = A + гдеA – условно взятая средняя величина (чаще всего в качестве условной средней берется Мо); ∑ - знак суммы; α – отклонение каждой варианты в интервалах от условной средней = p – частота (число раз, с которым встречается одна и та же варианта признака). αp – произведение отклонения (α) на частоту (p); n – число наблюдений, т.е. сумма всех частот или общее число всех вариант (∑p). i – величина интервала = Таким образом, средняя взвешенная вычисленная по способу моментов, составила 176,74 см., что практический совпало с расчетами средней обычным методом – 176,7 см.. Однако при вычислений средней по способу моментов используют простые цифры, вычисление менее громоздки, что значительно облегчает и ускоряет расчеты. Средняя арифметическая (средняя взвешенная) имеет ряд свойств, которые используют в некоторых случаях для упрощения расчета средней и получения ориентировочной величины. 1. Средняя арифметическая занимает срединное положение в строго симметричном вариационном ряду (M = M0 = Me). 2. Средняя арифметическая имеет абстрактный характер и является обобщающей величиной, выявляющей закономерность. 3. Алгебраическая сумма отклонений всех вариант от средней равна нулю: ∑ (V - M) = 0. На этом свойстве основан расчет средней по способу моментов. Таблица 7 Определение среднего роста студентов-мужчин 20-22 лет (Методика расчета средней арифметической величины по способу моментов, i = 5)
Коэффициент вариации Вариация — различие значений какого-либо признака у разных единиц совокупности за один и тот же промежуток времени. Причиной возникновения вариации являются различные условия существования разных единиц совокупности. Вариация — необходимое условие существования и развития массовых явлений.Определение вариации необходимо при организации выборочного наблюдения, статистическом моделировании и планировании экспертных опросов. По степени вариации можно судить об однородности совокупности, устойчивости значений признака, типичности средней, о взаимосвязи между какими-либо признаками. Коэффициент вариации (Cv) определяет изменчивость вариационного ряда в процентах и дает возможность судить о качественной однородности изучаемой совокупности. Коэффициент вариации является относительной мерой разнообразия, так как исчисляется как процентное отношение среднеквадратического отклонения (σ) к средней арифметической величине (M). Формула коэффициента вариации выглядит следующим образом: Cv = Для ориентировочной оценки степени разнообразия признака пользуются следующими градациями коэффициента вариации. Если коэффициент составляет более 20 %, то отмечают сильное разнообразие; при 20-10 % - среднее, и если коэффициент менее 10 %, то считают, что разнообразие слабое. Коэффициент вариации применяют при сравнении степени разнообразия признаков, имеющих различия в величине признаков или неодинаковую их размерность.
Глава 2
Таблица 8 Вопросы тестового контроля Применяются для изучения а) вероятных признаков, которые могут быть или не быть б) постоянных признаков, присущих всем единицам наблюдения
Используют формулу а) б) в) г)
008. Для вычисления ошибки для средних величин при большой выборке Используют формулу а) б) в) г)
ОБРАЗЕЦ ВЫПОЛНЕНИЯ ТИПОВОГО ЗАДАНИЯ Задание 1. Задача 1 Условие задачи: результаты измерения частоты дыхания (число дыхательных движений в минуту) у 8 мужчин в возрасте 35 лет: 20, 22, 18, 15, 16, 21, 24, 19.
Задание: на основе приведенных данных требуется: 1) составить простой вариационный ряд, 2) вычислить простую среднюю арифметическую (M).
Решение Поскольку в данном случае n Таблица 1 Частота дыхания (V)
Простую среднюю арифметическую определяем по формуле: M = Ответ: M = 19 дыхательных движений в минуту. Задача 2 Условие задачи: результаты измерения роста 10 мальчиков в возрасте 2 лет (в см.): 90, 92, 95, 91, 93, 96, 94, 98, 89, 97.
Задание:н а основе приведенных данных требуется: 1) составить простой вариационный ряд, 2) вычислить простую среднюю арифметическую (M). Решение Поскольку в данном случае n
Таблица 2 Результаты измерения роста
Простую среднюю арифметическую определяем по формуле: M = Ответ:M = 94 см. Задание 2. Задача 1 Условие задачи: результаты лихорадочного периода при пневмонии у 32 больных (число дней): 3, 8, 14, 14, 7, 6, 4, 12, 13, 3, 4, 5, 10, 11, 5, 10, 10, 11, 12, 8, 9, 7, 7, 8, 9, 9, 7, 8, 12, 6, 10, 9.
Задание: на основе приведенных данных требуется: 1) построить простой вариационный ряд, 2) найти моду (Mo) и медиану(Me), 3) вычислить взвешенную среднюю арифметическую (M).
Решение 1. Строим простой (несгруппированный) вариационный ряд, последовательно располагая варианты в порядке возрастания с соответствующими им частотами (табл. 3): 2. Находим моду (Mo): с наибольшей частотой встречается варианта, равная 8 дням, следовательно, Mo = 8. Находим порядковый номер медианы (Me) по формуле 3. Вычисляем взвешенную среднюю арифметическую (M) по формуле: M = M = Ответ: M = 8,5 дня. Таблица 3
Задача 2 Условие задачи: получены следующие данные состоящих на диспансерном учете больных язвенной болезнью желудка и двенадцатиперстной кишки у 45 участковых терапевтов: 15, 16, 28, 17, 18, 19, 15, 27, 29, 21, 29, 27, 29, 22, 26, 25, 25, 25, 25, 26, 26, 22, 18, 17, 20, 21, 28, 30, 16, 15, 18, 19, 20, 20, 20, 20, 20, 21, 21, 22, 20, 22, 23, 23, 23.
Задание: на основе приведенных данных требуется: 1) построить простой вариационный ряд, 2) найти моду (Mo) и медиану(Me), 3) вычислить взвешенную среднюю арифметическую (M).
Решение 1. Строим простой (несгруппированный) вариационный ряд, последовательно располагая варианты в порядке возрастания с соответствующими им частотами (табл. 4): Таблица 4
2. Находим моду (Mo): с наибольшей частотой встречается варианта, равная 20 Д/б, следовательно, Mo = 20. Находим порядковый номер медианы (Me) по формуле 3. Вычисляем взвешенную среднюю арифметическую (M) по формуле:
M = = Ответ: M = 22 Д/б.
ЗАДАЧА 3
Условие задачи: получены следующие данные о длительности лечения в стационаре 45 больных пневмонией (в днях): 25, 11, 12, 13, 24, 23, 23, 24, 21, 22, 21, 23, 22, 21, 14, 14, 22, 20, 20, 15, 15, 16, 20, 20, 16, 16, 20, 17, 17, 19, 19, 19, 18, 18, 18, 18, 19, 19, 17, 17, 18, 18, 19, 26, 26. Задание: на основе приведенных данных требуется: 1) построить простой вариационный ряд, 2) найти моду (Mo) и медиану(Me), 3) вычислить взвешенную среднюю арифметическую (M). 4) составить сгруппированный вариационный ряд; 5) вычислить среднюю арифметическую (M) по способу моментов; 6) определить среднее квадратическое отклонение.
Решение 1. Строим простой (несгруппированный) вариационный ряд, последовательно располагая варианты в порядке возрастания с соответствующими им частотами (табл. 5): 2. Находим моду (Mo): с наибольшей частотой встречается варианта, равная 18 дням, следовательно, Mo = 18. Находим порядковый номер медианы (Me) по формуле 3. Вычисляем взвешенную среднюю арифметическую (M) по формуле:
M =
=
Ответ: M =.19 дней. Таблица 5
4. Пользуясь предыдущими данными составляем сгруппированный вариационный ряд (табл. 6); 1) определяем размах ряда вычитанием минимальной варианты из максимальной, Vmax. –Vmin. 2) определяем число групп (поскольку n = 45, число групп берем равным 6 – (табл. 6); 3) находим интервал (i) по формуле:
i =
4) начиная с минимальной варианты, строят вариационный ряд. Границы интервалов должны быть четкие, исключающие попадание одной и той же варианты в разные группы.
Таблица 6
5) определяем границы и середину каждой группы: например, первая группа вариант при i = 3 будет 11-13 дней, середина группы – 12 дней, следующая – 14-16 дней, середина 15 дней и т.д.; 6) распределяем изучаемую совокупность по группам, указывая им соответствующие частоты (p); 5. Вычисляем среднюю арифметическую (M) по способу моментов по формуле; M = A+ Порядок вычисления представлен в таблице 7 (за условную среднюю принимаем Mo = 18 дням,i = 3). Подставляем полученные значения в формулу: M = A + Ответ: M = 19,1 дня. (средняя взвешенная вычисленная по способу моментов (19,1 дня), совпало с расчетами средней обычным методом (19 дней). 5. Среднее квадратическое отклонение
σ = i Таблица 7
При этом первый момент средней нам известен (формула 5), он равен 1,1,
Для определение второго момента средней ( Получаем, что Ответ: σ = 3,63 дня. Задание 3
ОПРЕДЕЛЕНИЕ ОШИБКИ (mM) И ДОВЕРИТЕЛЬНЫХ ГРАНИЦ СРЕДНЕЙ ПРИ МАЛОМ ЧИСЛЕ НАБЛЮДЕНИЙ Задача 1 Условие задачи: результаты измерения частоты дыхания (число дыхательных движений в минуту) у 8 мужчин в возрасте 35 лет: 20, 22, 18, 15, 16, 21, 24, 19. Задание: на основе приведенных данных требуется: 1) составить простой вариационный ряд, 2) вычислитьпростую среднюю арифметическую (M), 3) определить среднееквадратическоеотклонение (σ), 4) вычислить ошибку (mM), 6) определить доверительные границы средней (M) при P = 95 % и P = 99 %.
Решение
1. Поскольку в данном случае n Таблица 1 Частота дыхания (V)
2. Простую среднюю арифметическую определяем по формуле: M = Ответ: M = 19 дыхательных движений в минуту. 3. Среднее квадратическое отклонение (σ) при n
σ =
определяем σ (табл. 2): Таблица 2 Частота дыхания (V)
Заносим данные таблицы в формулу: σ = 4. Ошибка средней определяется по следующей формуле: mM= 5. Доверительный интервал (tm = △) средней величины (M) определяем путем нахождения доверительного коэффициента t по таблице Стьюдента (табл. 8): а) при P = 95 % и при n = 8 t = 2,3; следовательно tm (△) = 2,3 ∙ 1,1 = 2,5 дых.движ. в мин., M = 19
Задание 4.ОПРЕДЕЛЕНИЕ ДОСТОВЕРНОСТИ РАЗНОСТИ МЕЖДУ Задача 1
Условие задачи: требуется определить, имеется ли достоверное снижение частоты пульса и приближение ее к норме в группе студентов после экзамена, если известно, что средняя частота пульса M1 до экзамена составила 98,8 удара в минуту (mM1= 4 удара в минуту); после экзамена (M2) – 84 в минуту (mM2 = 5 ударов в минуту).
Задание: требуется оценить достоверность разности между двумя средними величинами (M1 и M2)
Решение Достоверность разности между средними величинами определяется по формуле: t = Вывод. Поскольку t Задача 2 Условие задачи: при изучении успеваемости студентов медицинского института - не работающих и сочетающие учебу с работой - были получены следующие данные: у неработающих средний балл M1 = 4,1 (mM1 =
Задание: требуется оценить достоверность разности между двумя средними величинами (M1 и M2).
Решение Достоверность разности между средними величинами определяется по формуле: t = Вывод. Значение критерия t = 4,5 соответствует вероятности безошибочного прогноза P
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 2864; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.38.176 (0.018 с.) |

 =
=  =
=  = 4,6 сек.
= 4,6 сек. , вычитая же ее из середины, получают конец группы. В нашем примере
, вычитая же ее из середины, получают конец группы. В нашем примере  Прибавив 2 к середине первой группы, получим 67 (начало группы), ее концом будет: 65-2 = 63 (см. табл. 3).
Прибавив 2 к середине первой группы, получим 67 (начало группы), ее концом будет: 65-2 = 63 (см. табл. 3). уд/мин.
уд/мин.
 = 76,9 уд/мин. (табл. 5).
= 76,9 уд/мин. (табл. 5). =76,9 уд/мин.
=76,9 уд/мин.
 ,
, =
=  =176,7см.(табл. 6).
=176,7см.(табл. 6). 162
162
 = 167
= 167
 = 172
= 172
 = 177
= 177
 = 182
= 182
 187
187
 =
= 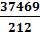 = 176,74 см.
= 176,74 см.




 * 100 %
* 100 %

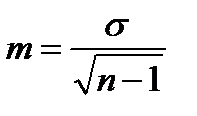

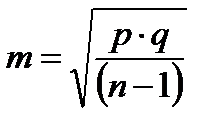
 30, а каждая варианта встречается один раз, строим простой вариационный ряд, располагая варианты в ранговом порядке (в порядке возрастания или убывания) (табл. 1):
30, а каждая варианта встречается один раз, строим простой вариационный ряд, располагая варианты в ранговом порядке (в порядке возрастания или убывания) (табл. 1): = 19 дыхательных движений в минуту. (1)
= 19 дыхательных движений в минуту. (1)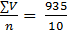 = 94см. (2)
= 94см. (2) =
= 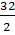 = 16, следовательно, 16-я по счету варианта является медианой. В нашем примере такой вариантой является 10, т.е, Me = 10 дням, Mo = 8 дням.
= 16, следовательно, 16-я по счету варианта является медианой. В нашем примере такой вариантой является 10, т.е, Me = 10 дням, Mo = 8 дням. (3)
(3)
 =
=  = 23, следовательно, 23-я по счету варианта является медианой. В нашем примере такой вариантой является 18, т.е, Me = 18 Д/б, Mo = 20Д/б.
= 23, следовательно, 23-я по счету варианта является медианой. В нашем примере такой вариантой является 18, т.е, Me = 18 Д/б, Mo = 20Д/б.
 Д/больных.
Д/больных.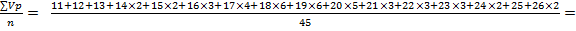
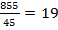 дней.
дней. =
= 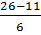 =
=  = 2,5
= 2,5 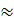 3; (4)
3; (4) ; (5)
; (5) = 18 +
= 18 + 
 в данном случае определяем по способу моментов по формуле (пользуемся предыдущими данными)
в данном случае определяем по способу моментов по формуле (пользуемся предыдущими данными) . (6)
. (6)
 = (1,1)2 = 1,21.
= (1,1)2 = 1,21. i2) необходимо заполнить построчно графу α2pв табл. 7; ∑ α2p = 72.
i2) необходимо заполнить построчно графу α2pв табл. 7; ∑ α2p = 72. = 1,6 * 9 = 14,4, подставляем полученные данные в формулу (6) и получаемσ =
= 1,6 * 9 = 14,4, подставляем полученные данные в формулу (6) и получаемσ =  =
=  = 3,63 дня.
= 3,63 дня. 30, а каждая варианта встречается один раз, строим простой вариационный ряд, располагая варианты в ранговом порядке (в порядке возрастания или убывания) (табл. 1):
30, а каждая варианта встречается один раз, строим простой вариационный ряд, располагая варианты в ранговом порядке (в порядке возрастания или убывания) (табл. 1):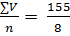 = 19 дыхательных движений в минуту. (1)
= 19 дыхательных движений в минуту. (1)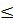 30 определяем по формуле:
30 определяем по формуле: , где d = V – M,
, где d = V – M, =
=  = 2,8 дых.движ. в мин.
= 2,8 дых.движ. в мин.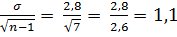 дых. движ. в мин.
дых. движ. в мин.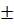 2,5 дых. движ. в мин, т. е. в генеральной совокупности при P = 95 % средняя величина числа дыхательных движений колеблется от 16,5 до 21,5 дых. движ. в мин.; при P = 99 % t = 3,3, tm (△) = 3,3 ∙ 1,1 = 3,6 дых. движ. в мин.; M = 19
2,5 дых. движ. в мин, т. е. в генеральной совокупности при P = 95 % средняя величина числа дыхательных движений колеблется от 16,5 до 21,5 дых. движ. в мин.; при P = 99 % t = 3,3, tm (△) = 3,3 ∙ 1,1 = 3,6 дых. движ. в мин.; M = 19  =
= 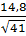 =
= 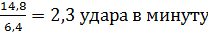 .
.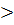 2,можно с вероятностью безошибочного прогноза больше 95 % утверждать, что после экзамена частота пульса у студентов снижается и приближается к норме.
2,можно с вероятностью безошибочного прогноза больше 95 % утверждать, что после экзамена частота пульса у студентов снижается и приближается к норме.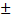 0,09), у сочетающих учебу с работой M2 = 3,65 (mM2 =
0,09), у сочетающих учебу с работой M2 = 3,65 (mM2 = 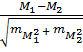 =
= 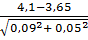 =
= 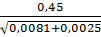 =
=  = 4,5.
= 4,5.


