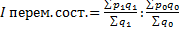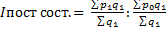Понятия о статистической средней величине.

Средняя величина – это обобщающий пок-ль, характеризующий типичный уровень явления в конкретных х места и времени, отражающий величину варирующего признака в расчете на единицу качественно однородной сов-ти.

Виды средней величины:

Степенные

*среднеарифметическая

*среднегармоническая

*среднеквадратическая

*среднегеометрическая

*среднехронологическая

Структурные

*мода

*медиана

Среднеарифметическая применяется в тех случаях когда объем варирующего признака для всей сов-ти явл суммой значения признаков отд-х её единиц. Х_=сумма xn/суммуn

Среднегармоническая применяется в тех случаях когда стат инф-ция не содержит частот (n) по отд-м вариантам Х. х_=суммаw/суммуw/x

Среднеквадратическая применяется в тех случаях когда возникает необходимость расчета среднего размера признака выраженного в кубических единицах измерения. Х_=корень из сумма Х2N/сумму n

Среднегеометрическая применяется для расчета среднего темпа роста в рядах динамики Х_=n корень из ПКц

Среднехронологическая применяется для средне моментного уровня ряда динамики. Х_=0.5*х1+х2+..+хn*0/5/n-1

Мода и медиана

Способы расчета средней.

Средняя гармоническая опред хар-ом взаимосвязи определяющего показателя с осредняемым:

*простая средняя гармоническая, если значения признаков одинаковы: х_=n/сумму 1/х

*средняя гармоническая взвешенная, если значения признака не равны: х_=суммаFi/сумму1/Хi*Fi

Используют когда известны значения признака и их общий объем, а частоты не известны.

Средняя геометрическая используется когда индивидуальные значения признака представлены в виде относит величин:

*простая средняя геометрическая х_=nкорень из NXi

*взвешенная средняя геометрическая: х_=сумма I корень NXi

 

20.Способы расчета моды.

Мода (Мо) – это значение случайной величины случающиеся с большей вероятность в дискретном вариационном ряду.

В интервальных рядах определяют: *модальный интервал – интервал, имеющий наибольшую частоту.*значение признака.

Мо=Хмо+Iмо* Fмо-Fмо-1/(Fмо-Fмо-1)+(Fмо-Fмо+1)

Хмо – начальная (нижняя) граница модального

Iмо – величина модального интервала

Fмо – кол. Частот (н), кт соответствуют модальному интервалу

Fмо-1 – кол частот предшествующих модальному интервалу

Fмо+1 – кол частот последующих за модальным интервалом.

Мода определяется по графику кт называется гистограмма.

Для дискретного ряда модой будет явл вариант с наибольшей частотой (размер мужской обуви, что пользуется наибольшим спросом).

 

Способы расчета медианы.

Медиана (Ме) – кт находится в середине вариационного ряда (т.е. делит ряд на 2 части).

В случае интервального вариационного ряда распределения значение медианы вычисляется по формуле:

Ме=Хме+Iме* 0,5*на сумму n – Sме-1/Fме

Хме – начальная граница медианного интервала

Iме – величина медианного интервала

Sме-1 – сумма накопленных частот предшествующий медианному интервалу

Fме – кол частот соответствующих медианному интервалу.

Медиана строится по графику куммулята.

В дискретном ряду распределения медиана находится непосредственно по накопленной частоте, соответствующей номеру медианы.

 

Понятия о вариации.

Вариация – это изменение (колеблемость, многообразие, изменяемость) величины признака у единиц сов-ти.

Вариация возникает в результате того, что индивид-е значения признака складываются под сово-ым влиянием разнообразных факторов кт в свою очередь по разному сочетаются в каждом конкретном случае. Вопрос 23

 

Меры вариации.

Показатели вариации делятся на 2 группы: абсолютные и относительные.

К абсолютным относятся размах вариации, среднее линейное отклонение, дисперсия и среднее квадратическое отклонение. Вторая группа пок-ей вычисляется как отношение абсолютных пок-ей вариации к средней арифметической (или медиане).

Относительным и пок-ми вариации явл-я коэф-ы осцилляции, вариации, относительное линейное отклонение.

Размах вариации – показывает насколько велико различие м/у единицами сов-ти, имеющими самое маленькое и самое большое значение признака. R=Xmax-Xmin. Р.в. – важный показатель колебимости признака, но не исчерпывающий его характеристику.

Среднее линейное отклонение применяется в качестве своего рода центра тяжести, вокруг кт происходят колебания, рассеяние значений признака. Вычисляется как средняя арифметическая из абсолютных значений отклонений вариант; дает обобщенную хар-ку степени колеблемости признака в сов-ти.

Дисперсия («6»2) – средний квадрат отклонений индивидуальных значений признака от их средней величины и вычисляется по формулам простой и взвешенной дисперсии.

Среднее квадратическое отклонение – это обобщающая хар-ка размеров вариации признака в сов-ти, выраж-я в ех же единицах измерения, что и признак (метры, тонны, рубли и т.д.)

 

Основная характеристика размаха вариации и среднего абсолютного отклонения.

Размах вариации – показывает насколько велико различие м/у единицами сов-ти, имеющими самое маленькое и самое большое значение признака. R=Xmax-Xmin. Р.в. – важный показатель колебимости признака, но не исчерпывающий его характеристику.

Среднее линейное отклонение применяется в качестве своего рода центра тяжести, вокруг кт происходят колебания, рассеяние значений признака. Вычисляется как средняя арифметическая из абсолютных значений отклонений вариант; дает обобщенную хар-ку степени колеблемости признака в сов-ти.

Среднелинейное отклон.(для несгруппирирован.данных: d=E(xi-xс черт.)/n, для сгруп.данных d=E|xi-xс черт.|*n/En

Основная характеристика дисперсии и среднего квадратного отклонения.

Дисперсия («6»2) – средний квадрат отклонений индивидуальных значений признака от их средней величины и вычисляется по формулам простой и взвешенной дисперсии.

Среднее квадратическое отклонение – это обобщающая хар-ка размеров вариации признака в сов-ти, выраж-я в ех же единицах измерения, что и признак (метры, тонны, рубли и т.д.)

Дисперсия (для несгруп. s^2=E(xi-xс черт)^2/n, для сгруп. s^2=E|xi-xс черт|^2*n/En)

Сред.квадр.откл. s^2=корень(s^2)

Коэф.вар.(Vs=s/x с черт.*100%)

26.Коэффициенты вариации.

Коэффициент вариации V – характеризует степень вариации признака.

Используют КВ для целей сравнения колебимости различных признаков одной и той же совокупности.

КВ характеризует сравнения колебимости одного и того же признака в нескольких сов-х

Измеряют КВ в % или коэф-х

Коэффициенты вариации:

1.коэф осцилляции – это отношение размаха вариации к средней величине признака. Vr=R/x_*100

2.коэф вариации – это отношение среднего квадратического отклонения к средней величине признака. Vs=S/x_*100

3.линейный коэф вариации – это отношение среднего линейного отклонения к средней величине признака. Vd=d/x_*100

 

Ряды динамики и их виды.

Ряд динамики – это ряд, расположенных в хронологической последовательности числовых значений стат-го показателя.

Каждый ряд динамики состоит из 2х элементов: 1.периоды времени, даты. 2.уровень ряда (числовая хар-ка того или иного периода времени).

Виды рядов динамики:

1.по содержанию: *ряд абсолютных величин *ряд относ-х величин *ряд средних величин

2.по факту времени: *интервальный (ряд уровни кт харак-т состояние явления за отдельный период времени). *моментный (ряд, уровни кт харак-т состояние явления на определенный период или момент времени). Особенность ряда закл-я в том, что в каждом последующем периоде времени (уровне ряда) частично или полностью содержится предыдущий уровень.

3.в зависимости от расстояния м/у уровнями ряды динамики подразделяются на ряды динамики с равностоящими уровнями и неравностоящими уровнями во времени.

4.в зависимости от наличия осн тенденции изучаемого процесса ряды динамики подразделяются на стационарные и нестационарные.

Показатели анализа рядов динамики:

Общие:

Абсолютный прирост(/\Уц(цепной)=yi-yi-1, Уб(базис.)=yi-уб) +/-

Темп роста (Кц=yi/yi-1, Кб= yi/уб) в %

Темп прироста (/\Кц=Кц-100, /\Кб=Кб-100)

Абсолютное содержание 1% прироста(А=/\Уц//\Кц)

Сред.пок-ли ряда динамики:

Сред.ур-нь ряда(д/интер-го и д/момент-го у счерт.=Еуi/n),

а) с разностоящими пер.вр. сред.хрон.(у с черт.=(1/2y1+y2+…1/2yn)/n-1)

б).с неравными интервалами(у=Еу*n/Еn)

Сред.абсолют.прирост(/\уц с черт.=Е/\уц/n)

Сред.темп роста(Кц с черт.=корень^n(Пкц), Пкц-произ.цепных темпов роста в %

Сред.темп прироста(Тпр с черт.=Кц с черт. – 100

 

Сущность индексов, их виды.

Индекс – это относительный пок-ль, харак-ий изменения величины какого-либо признака во времени, пространстве или по сравнению с каким-либо эталоном (план, прогноз, норматив).

Осн элементом индексного отношения явл индексируемая величина – это значение стат признака, изучение кт явл объектом наблюдения.

Все экономические индексы можно классифицировать по след признакам:

1.степень охвата явления – индексы бывают индивидуальные и сводные. Индивид-ые служат для хар-ки изменения отд-х элементов сложного явления. Сводные – для измерения динамики сложного явления, составные части кт непосредственно несоизмеримы;

2.база сравнения – на 2 группы: динамические и территориальные. 1-я отражает изменение явления вовремени. 2-я применяется для межрегиональных сравнений;

3.вид весов – индексы бывают с постоянными и переменными весами.;

4.форма построения – различают агрегатные и средние (арифметические и гармонические). Агрегатная форма общих индексов явл основной формой эконом индексов. Средние – производные, они получаются в результате преобразования агрегатных индексов;

5.характер объекта исследования -;подразделяются на количественные (объемные) и качественные показатели.

6.объект исследования – бывают производительности труда, себестоимости, физич объема продукции, стоимости продукции;

7.состав явления – индексы постоянного состава (фиксированного) и переменного состава;

8.период исчисления – подразделяются на годовые, квартальные, месячные, недельные

С помощью экон индексов решаются след задачи:

1.измерение динамики соц-экон явления за 2 и более периодов времени;

2.измерение динамики среднего экон пок-ля;

3.измерение соотношения пок-ей по разным регионам;

4.определение степени влияния изменений значений одних пок-ей на динамику других;

5.пересчет значения макроэкономических пок-ей из фактических цен в сопоставимые.

Индвидуальный индекс цен = ip=p1/po, индекс объема продукции iq=q1/q0, индекс себестоимости iz=z1/z0

p – цена

q – физ.объем или кол-во

p*q – выручка, товарооборот

z- себестоимость (z*q-затраты на произ-во)

t-трудоемкость

w-выработка

Индивидуальный индекс

В денежном выражении

Общий индекс цены

Общий индекс физического объема товара

Индекс переменного состава

Индекс постоянного состава

Индекс структурных сдвигов

 

 

Исходные положения теории общих индексов.

Индекс – это относительная величина, кт характеризуют изменение сложных соц-экон показателей во времени, в пространстве, по сравнению с планом.

Рассчитывается в форме: коэф, %,%о

Название индекса отражает его содержание, а числовое значение – интенсивность изменения или степень отклонения явления (индекс потреб цен в отчетном году сост 107%).

Общий индекс(измен-е всех элем слож.явл.)

· Ipq=Ep1q1/Epoqo (отчет.период/базис.)

· /\pq=Ep1q1-Epoqo(+/-)

· Ip=Ep1q1/Epoq1, /\p= Ep1q1-Epoq1

· Iq=Epoq1/Epoqo, /\q=Epoq1=Epoqo

Взаимосвясь:Ipq=Ip*Iq, Ip=Ipq/Iq, /\pq=/\p+/\q