Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства средней арифметическойСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Средняя арифметическая обладает рядом математических свойств, которые более полно раскрывают ее сущность и в некоторых случаях используются для упрощения ее расчетов. В статистическом анализе применяются следующие свойства средней арифметической: 1. сумма отклонений отдельных значений признака
Поэтому среднюю можно назвать центром распределения данных: значения ниже и выше средней величины взаимно уравновешиваются. 2. Произведение средней на сумму частот всегда равно сумме произведений вариантов
3. Если к каждому значению признака
4. Если каждое значение
5. Если все частоты (веса)
6. Сумма квадратов отклонений значений признака
7. средняя арифметическая суммы (разности) признаков равна сумме (разности) их средних арифметических. Метод моментов Для расчета средней арифметической в случае интервального ряда с равными интервалами применяется метод моментов (см. § 6.4). Свойства средней арифметической во многих случаях позволяют упростить расчеты на основе следующего алгоритма: 1. Из всех значений признака вычесть произвольную постоянную величину (А); 2. Разность сократить на общий множитель ( 3. Рассчитать момент первого порядка (
4. Формула средней арифметической взвешенной получит следующий вид:
Данный способ вычисления средней называется методом моментов (способ отсчета от условного нуля). В этой формуле: В качестве произвольной постоянной величины (А) обычно выбирают один из центральных вариантов ряда:
При нечетном числе интервалов в качестве общего множителя ( Средняя гармоническая Средняя гармоническая принципиально не отличается от средней арифметической, но является обратной по отношению к ней. Она применятся, когда изучаемые показатели являются взаимообратными, т.е. связаны между собой как Средняя гармоническая взвешенная применяется, когда статистическая информация не содержит частот по отдельным вариантам совокупности, а представлена как их произведение ( Пример 5.3. Рассчитать среднюю стоимость тура по трем направлениям на основе данных, представленных в табл. 5.2. Таблица 5. 2 Основные показатели деятельности туристской фирмы (данные условные)
Решение. В условии отсутствуют данные о количестве туров
Число туров косвенно определяется в знаменателе формулы: В этом случае формула средней арифметической приводит к неверному ответу, так как в расчет принимаются только три значения (10, 12 и 8 тыс. руб.) из 12-ти. Рассмотрим случаи применения других степенных средних величин. Средняя геометрическая применяется в анализе динамики для расчета среднего темпа роста. Средняя квадратическая наиболее широко используется при расчете показателей вариации, средней площади. Средняя кубическая применяется, когда необходимо сохранить неизменной сумму кубов индивидуальных величин (например, при расчете среднего объема).
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 654; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.170 (0.007 с.) |

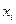 от средней арифметической
от средней арифметической  равна нулю:
равна нулю: (если частоты равны единице);
(если частоты равны единице); (если частоты различны).
(если частоты различны). :
:
 .
.
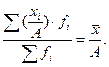

 <
< 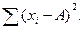
 );
); ) по формуле:
) по формуле: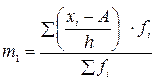 .
. =
=  + А.
+ А. - величина момента первого порядка;
- величина момента первого порядка; 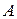 - центральный вариант ряда (условный 0).
- центральный вариант ряда (условный 0).
 и
и 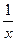 (например, затраты времени на единицу продукции и выработка продукции в единицу времени).
(например, затраты времени на единицу продукции и выработка продукции в единицу времени).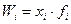 ).
).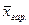 =
=  тыс. руб.
тыс. руб.