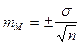Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление средней арифметической по способу моментовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
При большом числе наблюдений или при большом числовом значении вариант применяют упрощенный способ вычисления средней арифметической- способ моментов.
М = А+ iSар п где М - средняя арифметическая; А - условная средняя; i - интервал между группами вариант; S - знак суммирования.; а- условное отклонение каждой варианты от условной средней; р - частота встречаемости вариант; n - число наблюдений. Пример вычисления средней арифметической по способу моментов (средней массы тела юношей в возрасте 18 лет)
Этапы расчета средней по способу моментов: 1) за условную среднюю А рекомендуется принять Моду или Медиану, например А = 62кг, так как 62 кг было у 9 юношей из 25; 2) определяем "а" - условное отклонение варианты от условной средней, для этого из каждой варианты вычитаем условную среднюю: а = V - А, (например, а = 64 - 62 = +2 и т.д.). 3) умножаем условное отклонение "а" на частоту "р" каждой варианты и получаем произведение а р; 4) находим сумму Sа. р = - 10кг 5) рассчитываем среднюю арифметическую по способу моментов: М = А + i SаР = 62 - 1×0,4 = 61,6кг п Таким образом, можно сделать вывод, что в изучаемой нами группе юношей средняя масса тела 61,6 кг. Средняя арифметическая сама по себе ничего не говорит о том вариационном ряде, из которого она была вычислена. На ее типичность (достоверность) влияет однородность рассматриваемого материала и колеблемость ряда. Пример: даны два одинаковых по числу наблюдений вариационных ряда, в которых представлены данные измерений окружности головы детей в возрасте от 1 года до 2-х лет
Имея одинаковое число наблюдений и одинаковые средние арифметические (М= 46 см), ряды имеют различия в распределении внутри. Так варианты первого ряда отклоняются в целом от средней арифметической с меньшим значением, чем варианты второго ряда, что дает возможность предположить, что средняя арифметическая (46 см) более типична для первого ряда, чем для второго. В статистике для характеристики разнообразия вариационного ряда употребляют среднее
квадратическое отклонение (s) Существует два способа расчета среднего квадратического отклонения: среднеарифметический способ и способ моментов. При среднеарифметическом способе расчета применяют формулу:
где d истинное отклонение каждой варианты от истиной средней М. Формула используется при небольшом числе наблюдений (п <30) Формула для определения s по способу моментов:
где а - условное отклонение варианты от условной средней
Теоретически и практически доказано, что если при большом числе наблюдений к средней арифметической прибавить и отнять от нее 1s (М ± 1s), то в пределах полученных величин будет находится 68,3% всех вариант вариационного ряда. Если к средней арифметической прибавить и отнять 2s (М± 2s), то в пределах полученных величин будет находиться 95,5% всех вариант. М ±3s включает в себя 99,7% всех вариант вариационного ряда. Исходя из этого положения можно проверить типичность средней арифметической для вариационного ряда, из которого она была вычислена. Для этого надо к средней арифметической прибавить и от нее отнять утроенную s (М± 3s). Если в полученные пределы данный вариационный ряд укладывается, то средняя арифметическая типична, т.е. она выражает основную закономерность ряда и ей можно пользоваться. Указанное положение широко применяется при выработке различных стандартов (одежды, обуви, школьной мебели и т.д). Степень разнообразия признака в вариационном ряду можно оценить по коэффициенту вариации (отношение среднего квадратического отклонения к средней арифметической, умноженное на 100%)
Сv = s х 100 М При Сv менее 10% отмечается слабое разнообразие, при Сv 10-20% - среднее, а при более 20% - сильное разнообразие признака. Оценка достоверности реультатов статистического исследования
Как мы уже говорили, самые надежные результаты можно получать при применении сплошного метода т.е. при изучении генеральной совокупности. Между тем изучение генеральной совокупности связано со значительной трудоемкостью. Поэтому в медико-биологических исследованиях, как правило, проводятся выборочные
наблюдения. С тем, чтобы полученные при изучении выборочной совокупности данные можно было перенести на генеральную совокупность, необходимо провести оценку достоверности результатов статистического исследования. Выборочная совокупность может недостаточно полно представлять генеральную совокупность, поэтому выборочным наблюдениям всегда сопутствует ошибка репрезентативности. По размерам средней ошибки (m) можно судить, насколько найденная выборочная средняя величина отличается от средней генеральной совокупности. Малая ошибка указывает на близость этих показателей, большая ошибка такой уверенности не дает. На величину средней ошибки средней арифметической влияют следуюие два обстоятельства. Во-первых, однородность собранного материала: чем меньше разбросанность вариант вокруг своей средней, тем меньше ошибка репрезентативности. Во-вторых, число наблюдений: средняя ошибка будет тем меньше, чем больше число наблюдений. Средняя ошибка средней арифметической вычисляетсяя по следующей формуле: Средняя ошибка (ошибка репрезентативности) для относительных величин определяется по формуле: где mp - средняя ошибка показателя; р - показатель в % или в %о q - (100 -р), (1000 -р) n - общее число наблюдений Пример: Из лечебного учреждения выбыло 289 больных, из них умерло 12. Относительная величина (показатель летальности) р = (12:289)х100 = 4,1%; q=100 -р = 100-4,1 =95,9, откуда mp = ± Таким образом, относительная величина при повторном исследовании будет соответствовать 4,1 ±1,16% Доверительные границы - это максимальное и минимальное значение в пределах которого при заданной степени вероятности безошибочного прогноза может находиться относительный показатель или средняя величина в генеральной совокупности Доверительные границы относительной величины в генеральной совокупности определяют по формуле: Рген = Рвыб ± tmm Доверительные границы средней арифметической в генеральной совокупности определяется по формуле: Мген = Мвыб ± tmm где Рген и Мген - значения относительной и средней величины, полученные для генеральной совокупности. Рвыб и Мвыб - значения относительной и средней величины, полученные для выборочной совокупности. mр и mm - ошибка репрезентативности для средних и относительных величин. t - критерий достоверности. Установлено, что если t= 1, достоверность не превышает 68%; если t=2 -95%; если t=3- 99% При медицинских и биологических исследованиях считается достаточным, если критерий достоверности t ³ 2(достоверность 95%) Чтобы найти критерий t при числе наблюдений £ 30 необходимо воспользоваться специальной таблицей С уменьшением величины ошибки репрезентативности уменьшаются доверительные границы средних и относительных величин, т.е.уточняются результаты исследования, приближаясь к соответствующим величинам генеральной совокупности. Если ошибка репрезентативности большая, то получают большие доверительные границы, которые могут противоречить логической оценке искомой величины в генеральной совокупности. Доверительные границы зависят также от избранной исследователем степени вероятности безошибочного прогноза. При большой степени вероятности безошибочного прогноза размах доверительных границ увеличивается.
|
||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 3041; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.141.201 (0.01 с.) |



 ;
;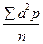 момент второй степени, а
момент второй степени, а 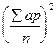 момент первой степени, возведенный в квадрат.
момент первой степени, возведенный в квадрат.