
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
За 2000-2115 гг. Методом скользящей среднейСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Недостаток метода простой скользящей средней состоит в том, что сглаженный ряд динамики сокращается ввиду невозможности получить сглаженные уровни для начала и конца ряда. Этот недостаток устраняется применением метода аналитического выравнивания для анализа основной тенденции. Аналитическое выравнивание предполагает представление уровней данного ряда динамики в виде функции времени - y=f(t). Для отображения основной тенденции развития явлений во време-ни применяются различные функции: полиномы степени, экспоненты, логистические кривые и другие виды. Полиномы имеют следующий вид: полином первой степени полином второй степени полином третьей степени полином n-ой степени. Здесь а0; а1; а2;... аn - параметры полиномов, t - условное обозначение времени. В статистической практике параметры полиномов невысокой степени иногда имеют конкретную интерпретацию характеристик динамического ряда. Так, параметр а0 трактуется как характеристика средних условий ряда динамики, параметры а1, а2, а3 - как изменения ускорения. t После выбора вида уравнения необходимо определить параметры уравнения. Самый распространенный способ определения параметров уравнения - это метод наименьших квадратов. Согласно этому методу, для нахождения параметров полинома n-й степени необходимо решить систему так называемых нормальных уравнений, но для упрощения ее решения используют метод кодировки для: системы отсчета времени "t". Причем эта система выбирается таким образом, чтобы Например: Годы 2000 2001 2002 2003 2004 2005 2006 Значение"t". -3 -2 -1 0 +1 +2 +3 Если число уровней ряда четное, то вместо нуля в центре мы поставили бы единицы с противоположными знаками у двух уровней, находящихся в середине ряда. Тогда разница между годами составляла бы две единицы времени и общий вид систем был бы таким (например, для ряда из 6 уровней): 2001 2002 2003 2004 2005 2006 -5 -3 -1 +1 +3 +5 В случае применения упрощенной системы отсчета времени параметры уравнения находятся по упрощенным формулам:
При сглаживании ряда динамики по показательной кривой yt=a0a1t
Важное место в системе методов прогнозирования занимают статистические методы. Применение прогнозирования предполагает, что закономерность развития, действующая в прошлом (внутри ряда динамики), сохранится и в прогнозируемом будущем, то есть прогноз основан на экстраполяции. Экстраполяция, проводимая в будущее, называется перспективой и в прошлое - ретроспективой. Обычно, говоря об экстраполяции рядов динамики, подразумевает чаще всего перспективную экстраполяцию. В зависимости от того, какие принципы и какие исходные данные положены в основу прогноза, можно выделить следующие элементарные методы экстраполяции: среднего абсолютного прироста, среднего темпа роста и экстраполяция на основе выравнивания рядов по ка-кой-либо аналитической формуле. Прогнозирование по среднему абсолютному приростуможет быть выполнено в том случае, если есть уверенность считать общую тенденцию линейной, то есть метод основан на предположении о равномерном изменении уровня (под равномерностью понимается стабильность абсолютных приростов): к последнему уровню прибавляется средний абсолютный прирост умноженный на период экстраполяции. Прогнозирование по среднему темпу роста можно осуществлять в случае, когда есть основание считать, что общая тенденция ряда характеризуется показательной (экспоненциальной) кривой. Для нахождения тенденции в этом случае необходимо средний коэффициент роста, возведенный в степень, соответствующую пределу экстраполяции умножить на последний уровень. При аналитическом выражение трендадостаточно продолжить значения независимой переменной времени (t). Тесты
1. Установите содержание задачи, решаемой путем анализа рядов динамики: A. измерение уровня вариации явлений; B. анализ территориальных пропорций; C. анализ процесса развития явления во времени; D. иная задача.
2. В числе нижеприведенных динамических рядов выделите интервальный ряд: A. численность поголовья крупного рогатого скота на начало каждого года; B. размер основных фондов на 1-ое июля каждого года, млн. руб.; C. валовой сбор зерна за ряд лет, млн. руб. D. число крестьянских фермерских хозяйств на конец каждого года, единиц.
3. Укажите правильный ответ расчета темпа прироста фондовооруженности труда по одной из машиностроительных фирм в 2004 году по сравнению с 2003 годом, если фондовооруженность труда в 2003году составила 14,3 тыс. руб., а в 2004 году – 15,7 тыс. руб.: A. B. C. D.
4. Укажите правильный ответ расчета цепного показателя абсолютного прироста, если известна динамика среднегодовой численности работников предприятия: 2000 г. – 1180 чел, 2001 г. – 1250 чел., 2002 г. – 1243 чел., 2003 г. – 1315 чел., 2004 г. – 1396чел. A. 1315 - 1180 = 135; B. 1396 - 1250 = 146; C. 1396 – 1315 = 81; D. 1243 - 1180 = 63.
5. Укажите правильный ответ расчета цепного темпа роста ввода в действе жилых домов предприятиями всех форм собственности региона, если известны следующие данные (млн. м2 общей площади): 2001 г. – 21, 2002 г. – 20, 2003 г. – 22, 2004 г. – 23: A. B. C. D.
6. Укажите правильный ответ расчета абсолютного значения одного процента прироста производства автомобилей в регионе по данным за 2003 г. – 1602 тыс. шт., в 2004 г. – 1846 тыс. шт.: A. B. C. D.
7. Какой из способов вычисления среднегодовой численности установленного оборудования методически является наиболее обоснованным, если задан ряд динамики о численности единиц установленных в цехе шлифовальных станков на начало каждого месяца: A. B. C. D.
8. Какой из способов исчисления среднегодовой численности работников предприятия является методически наиболее обоснованным, если задан ряд динамики среднегодовой численности предприятия за 2000-2004гг.: A. средняя геометрическая; B. средняя арифмитическая; C. средняя гармоническая; D. средняя хронологическая моментного ряда динамики.
9. Назовите вариант ответа, содержащий наибольшее число характерных для динамических рядов приемов их обработки. A. Укрупнение интервалов, приведение к одному основанию, сглаживание, интерполяция, экстраполяция. B. Простое укрупнение интервалов, долевая перегруппировка, взвешивание, сглаживание, смыкание, аналитическое выравнивание, вычисление процентных отношений. C. Укрупнение интервалов, способ характеристики средними величинами, сглаживание. D. Применение способа моментов, укрупнение интервалов, взвешивание, перегруппировка, вычисление показателей сравнения, выравнивание по способу наименьших квадратов, интерполяция.
10. Определите число расчетных уровней ряда динамики, если произведено сглаживание ряда, состоящего из 13 уровней по способу скользящей средней, период которой равен 5: A. 13; B. 10; C. 9; D. 8.
11. Сколько уровней ряда динамики будет потеряно при сглаживании по скользящей средней, период которой равен 4? A. число уровней ряда не изменится; B. 4; C. 3; D. иной ответ.
12. Какие значения может принимать период скользящей средней?: A. нечетные; B. четные; C. четные и нечетные; D. иной вариант ответа.
13. Какую разновидность способов обработки рядов динамики следует использовать при постановке задачи на изучение динамики значений признака, характеризующего изменившийся круг учитываемых объектов: A. укрупнение интервалов; B. сглаживание; C. аналитическое выравнивание; D. смыкание.
14. Что собой представляет операция интерполяции рядов динамики? A. Нахождение перспективных значений уровней ряда динамики; B. Нахождение значений неизвестного уровня внутри ряда; C. Нахождение значения неизвестного уровня за пределами ряда. D. Иной ответ.
15. Показатель абсолютного значения одного процента прироста равен: A. уровню ряда, деленному на темп прироста; B. уровню ряда, взятому за базу сравнения, деленному на 1000; C. абсолютному приросту, деленному на темп прироста; D. абсолютному приросту, деленному на темп роста.
16. Темп прироста исчисляется как: A. разность уровней ряда; B. отношение уровней ряда; C. отношение абсолютного прироста к уровню ряда, взятому за базу сравнения; D. отношение абсолютного прироста к темпу роста.
17. Абсолютный прирост перевозок всеми видами транспорта в России показывает: A. на сколько млн. т. увеличился (уменьшился) объем перевозок; B. на сколько процентов увеличился (уменьшился) объем перевозок; C. во сколько раз увеличился (уменьшился) объем перевозок; D. средний уровень перевозок.
18. Темп роста производства стиральных машин в регионе показывает: A. на сколько тыс.шт. увеличилось (уменьшилось) производство машин; B. на сколько процентов увеличилось (уменьшилось) производство машин; C. во сколько раз увеличилось (уменьшилось) производство машин; D. средний уровень ряда.
19. Темп прироста парка тракторов в стране показывает: A. на сколько тыс.шт. увеличился (уменьшился) парк тракторов; B. во сколько раз увеличился (уменьшился) парк тракторов; C. на сколько процентов увеличился (уменьшился) парк тракторов; D. среднюю численность тракторов.
20. Базисный абсолютный прирост равен: A. сумма цепных абсолютных приростов; B. произведение цепных абсолютных приростов; C. разности цепных абсолютных приростов; D. деление последующих на предыдущие абсолютные приросты.
21. Средний абсолютный прирост равен: A. разности конечного и начального уровней, деленной на число уровней ряда; B. конечному базисному абсолютному приросту, деленному на число цепных абсолютных приростов; C. полусумма конечного и начального уровней; D. отношению конечного уровня на начальный уровень.
22. Средний темп роста вычисляется как: A. средняя арифметическая; B. средняя хронологическая; C. средняя геометрическая; D. средняя гармоническая.
23. Тенденция представляет собой изменение ряда динамики: A. равномерно повторяющееся через определенные промежутки времени внутри ряда; B. определяющие какие-то общее направление развития; C. равномерно повторяющееся через определенные промежутки времени с годичным интервалом; D. изменения, являющиеся результатом действия большого количества относительно слабых второстепенных факторов.
24. Аналитическое выравнивание позволяет: A. измерить структуру совокупности; B. выявить основную тенденцию развития явления; C. получить количественные характеристики изменения уровней ряда; D. изучить взаимосвязи явлений. E.
25. Ряд динамики, характеризующий изменение урожайности сахарной свеклы в хозяйстве, аналитически можно представить уравнением A. B. 12ц/га; C. 242ц/га; D. 112%.
26. Определение неизвестных промежуточных уровней ряда динамики называется: A. интерполяцией; B. экстраполяцией; C. сглаживанием; D. взвешиванием.
27. Экстраполяция может производиться на основе выявленной: A. тенденции развития ряда динамики; B. корреляционной зависимости между показателями; C. сезонной компоненты ряда динамики; D. случайно компоненты ряда динамики.
28. Базисный абсолютный прирост равен: а) сумме цепных абсолютных приростов; б) произведению цепных абсолютных приростов. A. а; B. б; C. а,б; D. -.
29. Базисный темп роста равен: а) сумме абсолютных темпов роста; б) произведению цепных темпов роста. A. а; B. б; C. а,б; D. -.
Пример Рассмотрим для примера расчет аналитических показателей,динамики по следующим данным: Число зарегистрированных крестьянских (фермерских) хозяйств в Российской Федерации
На основе этих данных необходимо рассчитать абсолютные приросты. темпы роста и прироста, средний уровень ряда, средний темп роста и прироста, а также абсолютное значение одного процента прироста. Для расчета абсолютного прироста необходимо из уровня каждого последующего года вычесть уровень предыдущего или начального года (или какого-либо другого, принятого за базу сравнения). Так, например, абсолютный прирост в 1995г. по сравнению с 1994г. составил 279,2-270,0=9,2тыс.,а по сравнению с начальным - 1991г. 279,2-4,4 = 274,8тыс. Темп роста представляет собой отношение уровня последующего года к уровню предыдущего или начального. Так для 1995г. темп роста по сравнению с 1994г. составил (279,2:270,0)-100 = 103,4%, а по сравнению с 1991 г. (279,2:4,4) • 100 = 634,5%. Темп прироста есть отношение абсолютного прироста к предыдущему или начальному уровню (или какому-либо другому, принятому за базу сравнения). Для 1995г. по сравнению с 1994г. темп роста равен (9,2:270,0)-100=3,4% или 103,4-100=3,4%. Абсолютное значение одного процента прироста получается в результате деления абсолютного прироста по сравнению с предыдущим периодом на соответствующий темп роста, выраженный в процентах. Приведем в таблице результат расчета всех этих показателей анализа ряда динамики
Рассчитаем также средние показатели. Средний уровень ряда динамики числа фермерских хозяйств рассчитывается по формуле средней арифметической простой, поскольку данный ряд интервальный: Столь же просто находится средний абсолютный прирост:
Для расчета среднего темпа роста используем среднюю геометрическую:
Следующей проблемой изучения динамики является выявление основной тенденции, то есть главного направления в изменении изучаемого явления. Речь идет о случаях скрытой тенденции, присущей тому или иному ряду динамику. Например, за колебаниями уровней урожайности какой-либо сельскохозяйственной культуры в отдельные годы тенденция роста урожайности может не просматриваться непосредственно, и поэтому должна быть выявлена статистически. Из различных методов выявления тенденции, обычно рассматриваемых в учебной литературе (укрупнение интервалов, механическое сглаживание, аналитическое выравнивание), обратите особое внимание на последний. Необходимо учитывать, что аналитическое выравнивание представляет собой частный случай применения метода регрессии к анализу социально-экономических явлений. Этот метод заключается в том, что уровни ряда динамики представляются как функция времени (t):
В качестве примера произведем выравнивание данных о выплавке чугуна по уравнению прямой Таблица 14 Таблица исходных данных и расчетных данных (цифры условные)
Пояснения к таблице. Первые две графы - исходные уровни ряда динамики дополняются графой, в которой показана система отсчета времени "t". Причем эта система выбирается таким образом, чтобы Если число уровней ряда четное, то вместо нуля в центре мы поставили бы единицы с противоположными знаками у двух уровней, находящихся в середине ряда. Тогда разница между годами составляла бы две единицы времени и общий вид систем был бы таким (например, для ряда из 6 уровней): 1990 1991 1992 1993 1994 1995 -5 -3 -1 +1 +3 +5 В случае применения упрощенной системы отсчета времени параметры уравнения находятся по упрощенным формулам:
Таким образом, уравнение, выражающее тенденцию роста выплавки чугуна, имеет вид: На основе этого уравнения находятся выравненные годовые уровни путем подстановки в него соответствующих значений "t" (они показаны в последней графе таблицы, причем общий объем выплавки чугуна остался неизменным).
Задания для самостоятельной работы Задача 1. Вычислите цепные и базисные абсолютное приросты, темпы роста и прироста, а также абсолютные значения 1% прироста по следующим данным:
Задача 2. По данным задачи N1 рассчитайте средние показатели ряда динамики за 1991-1996 гг.: средний валовой сбор, средний абсолютный прирост валового сбора, средний темп роста и прироста. Задача 3. Произведите обработку ряда динамики закупок картофеля в области методом: а) укрупнения интервалов; б) скользящей средней:
Задача 4. Темпы роста выпуска изделия "А" в отрасли составили: в 1994 г. - 101%, 1995 г. - 103%, 1996 г. - 84%. Определите средний годовой темп прироста за 1994-1996 гг.: Задача 5. Исчислите средние товарные запасы за I и II кварталы и за полугодие в целом по нижеследующим данным:
. Задача 6. На основании приведенных данных сделайте анализ внутригодовой динамики о реализации картофеля на рынках города; выявите сезонность покупательского спроса на эти продукты, предварительно выравнив ряд по прямой (тыс. ц): (цифры условные)
.
Тема 9. Индексы динамики Индексы В предыдущей теме речь шла о динамических рядах, в рамках которых был рассмотрен вопрос о темпах роста статистических показателей, отражающих определенные социально-экономические явления. Относительные величины получаемые путем сравнения одноименных показателей во времени в практике экономических исследований и сравнений, часто называют индексами, индексами также называют относительные величины, характеризующие соотношения показателей в пространстве, времени или темпах изменений экономических показателей, которые представляют практический интерес. С помощью индексов можно определить количественные изменения самых различных показателей функционирования народного хозяйства, развития социально-экономических процессов и т.п. В экономической работе с помощью индексов можно объективно и точно показать изменения в росте или снижении производства, изменения в урожайности, состоянии себестоимости и цен выпускаемой продукции, численности работающих, производительности труда, заработной платы, изменения в цене акций на фондовых рынках (индекс Доу Джонса), сравнительная характеристика изменения погоды за определенный период времени (температуры, влажности, давления) и т.д. и т.п. Все это говорит о широком диапазоне применения индексов в научной и практической деятельности экономических и других организаций и учреждений. Индексы в своей основе представляют разновидность относительных величин, характеризующих средние показатели исследуемых процессов или явлений в социально-экономических и других областях деятельности общества. Однако от средних величин,, индексы отличаются тем, что они воплощают в себе, как правило, сводные, обобщающие показатели, т.е. выражают собой некоторое содержание свойственное всем рассматриваемым явлениям и процессам. Например, предприятие, выпускающее многообразную продукцию, нельзя оценить путем сравнения изменения объемов производства с помощью простого сложения единиц выпускаемой продукции. Необходим какой-то общий измеритель, таким измерителем становится стоимость или себестоимость. При всем разнообразии индексы можно подразделить на две группы. Одни показатели выражаются абсолютными величинами свойственными всем единицам статистической совокупности. Другие представляют собой показатели, рассчитанные на какую-то единицу (показатели цен, себестоимости, производительности труда, заработной платы и т.п.). Условно первая группа показателей называется количественными и вторая группа условно называется качественными показателями. -q - количество (объем) товара в натуральном выражении -p цена единицы товара -z себестоимость единицы продукции -w выработка продукции в стоимостном выражении на одного рабочего или в единицу времени -v выработка продукции в натуральном выражении на одного рабочего или в единицу времени -T общие затраты времени (tq) или численность рабочих -pq стоимость продукции или товарооборот -zq издержки производства Классификация индексов: 1. по сложности: индивидуальные и агрегатные (простые взвешенные); 2. по характеру базы: с постоянной базой (базовые) и с переменной базой (цепные); 3.по характеру весов: с постоянными весами и с переменными весами (оценивающие влияние индексируемого показателя весов и. оценивающие влияние структурных сдвигов (весов)); 4. по виду индексируемого показателя (индекс цен, физического объема, себестоимости, товарооборота и.т.д.) 5. по сфере использования (для анализа АХД и биржевые) Индексы качественных показателей, которые рассчитываются на физическую единицу (цены, себестоимость, теплотворность единицы энергоресурса и т.д.), определяется в форме единичных показателей, а также в форме общих (групповых) индексов, характеризующих изменения индексируемого показателя в целом по избранной совокупности статистических данных. Индивидуальные индексы: характеризуют изменение отдельных единиц совокупности Чтобы различать, к какому периоду относятся индексируемые величины, принято возле символа внизу ставить знаки: "1" - для сравниваемых (отчетных) периодов и "0" - для тех периодов, с которыми производится сравнение (базисных). Например, при сравнении продукции произведенной в 2008 г. с продукцией 2009 г., то объем продукции в 2009 г. условно обозначают через q1, а продукции 2008 г. - q0, а соответствующий индивидуальный индекс динамики объема производства будет iq=q1 / q0; индивидуальный индекс динамики себестоимости единицы продукции iz=z1/z0; индивидуальный индекс динамики производительности труда по выработке iB=B1/B0 и по трудоемкости и it=t1/t0.; индивидуальный индекс динамики фондоотдачи iф=ф1/ф0; индивидуальный индекс выполнения планового задания Если рассчитывается индекс для нескольких периодов, то по существующим правилам обозначение, у каждой индексируемой величины, отнесенной к тому или иному периоду, ставится соответствующий знак. Например, данные о количестве произведенной продукции за 5 лет следует обозначить как q1, q2, q3, q4, q5 и в соответствии с этим рассчитывать предлагаемые индексы как базисные или цепные. Их отличие состоит в том, что за базовый нулевой показатель в одном случае берется предыдущий показатель (xt-1), а в другом фиксированный (x0). Агрегатные индексы обозначаются символом J; в числителе и знаменателе содержаться соединенные наборы (агрегаты) элементов изучаемой совокупности. Числитель и знаменатель агрегатного индекса представляет собой сумму произведений двух величин, одна из которых меняется (индексируемая величина), а другая остается неизменной и в числителе и в знаменателе(вес индекса). Наиболее типичным индексом количественного показателя является индекс объема, т.е. индекс физического объема продукции. Неоднородную продукцию необходимо соизмерить с помощью общих единиц измерения, после чего определить общий объем проданной продукции в отчетном и базисном периодах, найти их соотношение. Для достижения сопоставимости разнородных единиц вводится специальные сомножители индексируемых величин. В качестве такого соизмерителя в практике наших дней используют цену единицы продукции, с помощью чего измеряется объем произведенной несоизмеримой по физическим свойствам продукции. Индекс физического объема продукции показывает во сколько раз возросла (уменьшилась) стоимость продукции из-за роста (снижения) объемов производства. Если вычислить разность числителя и знаменателя Предположим, стоимость продукции определенного предприятия в базисном периоде (p0q0) 1997 г. составляла 125.000 рублей, а стоимость продукции, произведенной в отчетном периоде p0q1 (1998 г.) составила 155.000 рублей, то общий индекс физического объема будет представлен в следующем виде: 155000/125000=1,24 т.е. общий выпуск продукции в отчетном периоде по сравнению с базисным увеличился на 24%. Вычитая из числителя индекса знаменатель, получим 155.000 - 125.000 = 30.000 руб. Полученные числовые данные свидетельствуют о том, что за счет увеличения объема производства на 24% стоимость продукции в абсолютном выражении в отчетном периоде увеличилась на 30.000 рублей. Индекс стоимости продукции или товарооборота: Индекс цен – индекс качественного показателя. Индексируемая величина –цена, в качестве веса берется количество товаров отчетного периода. По статистическим данным полученным в результате определения агрегатного индекса цен мы имеем дополнительную экономическую информацию, а именно: во-первых, вычитая из числителя формулы знаменатель можно определить сумму прибыли или убытка, которую получает продавец от реализации отчетного периода за счет повышения или снижения цен. Во-вторых, если товарооборот (стоимость) определяется как произведение цены на количество произведенных единиц товара, то и произведение индекса цен на индекс объема должно давать индекс стоимости (товарооборота), т.е. Индексы структурных сдвигов Под изменением структуры явления понимается изменение доли отдельных групп единиц совокупности в общей их численности. Агрегатный индекс цен рассчитанный на основе неизменного объема произведенной продукции (данные отчетного периода) является индексом фиксированного состава Индекс структурных сдвигов показывает влияние структурных изменений на динамику средней цены. Он рассчитывается по формуле: Индекс переменного состава отражает изменение не только индексируемой величины (в данном случае цена), но влияние структуры совокупности (весов).
Между этими индексами существует следующая взаимосвязь:
Средние индексы Используются в том случае, когда нет возможности рассчитать общий агрегатный индекс, т.е существует недостаток в данных, тогда подставляют индивидуальный индекс Цепные и базисные индексы Система базисных индексов –это ряд последовательно вычисленных индексов одного и того же явления с постоянной базой сравнения, т.е. в знаменателе всех индексов находится индексируемая величина базисного периода Базисные индексы цен с постоянными весами - - Система цепных индексов – это ряд индексов одного и того же явления, вычисленные с меняющейся от индекса к индексу базой сравнения -
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 939; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.228.195 (0.015 с.) |




 +…+
+…+ .
. -для полинома 1 –ой степени
-для полинома 1 –ой степени для полинома 2-ой степени
для полинома 2-ой степени
 или 109,8%;
или 109,8%;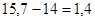 ;
;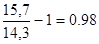 ;
; .
. или110%;
или110%; или 115%;
или 115%; или 104,8%;
или 104,8%;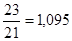 или 104,5%.
или 104,5%. ;
; ;
; ;
; .
. ;
; ;
; ;
; .
. . Это значит, что урожайность сахарной свеклы увеличивается ежегодно в среднем на:
. Это значит, что урожайность сахарной свеклы увеличивается ежегодно в среднем на: 12%;
12%;

 или 100,9%
или 100,9%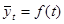

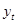
 (млн.т)
(млн.т)



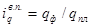 .
. Допустим, нам необходимо оценить изменения в производстве продукции определенного предприятия или группы предприятий за определенный период времени. Рассматриваемые предприятия производят разнообразную, т.е. несопоставимую по потребительским свойствам продукцию.
Допустим, нам необходимо оценить изменения в производстве продукции определенного предприятия или группы предприятий за определенный период времени. Рассматриваемые предприятия производят разнообразную, т.е. несопоставимую по потребительским свойствам продукцию. , то итог (в абсолютных единицах) покажет, на сколько рублей изменилась стоимость продукции в результате изменения объемов производства.
, то итог (в абсолютных единицах) покажет, на сколько рублей изменилась стоимость продукции в результате изменения объемов производства. показывает, во сколько раз возросла стоимость продукции (товарооборота) по сравнению с базисным периодом. Разность числителя и знаменателя
показывает, во сколько раз возросла стоимость продукции (товарооборота) по сравнению с базисным периодом. Разность числителя и знаменателя 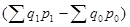 , покажет, на сколько рублей изменилась стоимость продукции (товарооборот) в текущем периоде по сравнению с базисным.
, покажет, на сколько рублей изменилась стоимость продукции (товарооборот) в текущем периоде по сравнению с базисным.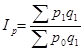 , числитель –стоимость товара в отчетном периоде, знаменатель – условная стоимость того же количества товаров, но по ценам базисного периода. Индекс цен показывает во сколько раз уменьшилась () стоимость продукции из-за изменения цен. Разность числителя и знаменателя
, числитель –стоимость товара в отчетном периоде, знаменатель – условная стоимость того же количества товаров, но по ценам базисного периода. Индекс цен показывает во сколько раз уменьшилась () стоимость продукции из-за изменения цен. Разность числителя и знаменателя  , покажет, на сколько рублей изменилась стоимость продукции в результате роста (снижения) цен в текущем периоде по сравнению с базисным. Изменение физических объемов не имеет значение.
, покажет, на сколько рублей изменилась стоимость продукции в результате роста (снижения) цен в текущем периоде по сравнению с базисным. Изменение физических объемов не имеет значение. Указанная ранее схема определения агрегатных индексов может использоваться при расчете различных аналитических индексов: индекс издержек производства
Указанная ранее схема определения агрегатных индексов может использоваться при расчете различных аналитических индексов: индекс издержек производства  ; индекс затрат времени на производство продукции:
; индекс затрат времени на производство продукции: 
 - этот индекс называется индексом Пааше.
- этот индекс называется индексом Пааше.


 среднеарифметический индекс: цен -
среднеарифметический индекс: цен -  , среднегармонический индекс цен –
, среднегармонический индекс цен –  ,
,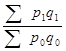 ;
;  ; …
; …  - индекс стоимости, базисные индексы цен -
- индекс стоимости, базисные индексы цен -  ;
;  ; …
; …  - это индексы с переменными весами.
- это индексы с переменными весами. ;
; 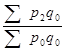 ; …
; … 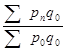
 ; …
; …  , цепной индек
, цепной индек 


