
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оптимальная численность выборкиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте При проведении выборочных исследований в торговле для определения характеристик выборки часто образцы разрушаются, поэтому нормы отбора образцов в выборку должны быть минимальными. Это связано еще и с тем, что необходимо получить достоверные сведения с минимальными затратами времени и труда. Поэтому вопрос о оптимальности численности выборки имеет важное практическое значение. Повышение процента выборки, как правило ведет к снижению погрешностей, но увеличивает затраты. следовательно, необходимо учитывать две проблемы при организации выборочного обследования. Формулы необходимого объема выборки для различных способов формирования выборочной совокупности могут быть выведены из соответствующих соотношений, используемых при расчете предельных ошибок выборки
ВОПРОСЫ 1. В чем отличие выборочного наблюдения от других видов несплошного наблюдения? 2. Что такое ошибка выборки? 3. В чем состоят основные проблемы теории выборочного наблюдения? 4. Какие вы знаете способы отбора единиц из генеральной совокупности? 5. Назовите основные способы распространения выборочных данных на генеральную совокупность. 6. Назовите особенности планирования выборочного обследования и его основные этапы.
Пример решения
Рассмотрим решение типовых задач по выборке. Задача 1. В результате выборочного наблюдения затрат времени на изготовление некоторых деталей получены следующие данные: Таблица
Требуется: 1. Определить выборочные характеристики: средние затраты времени на изготовление одной детали и долю деталей, на которые затрачивается до 24 мин. 2. Вычислить средние ошибки этих показателей. 3. Рассчитать с вероятностью 0,954 предельные ошибки.и границы нахождения генеральных характеристик. Решение. На основе ряда распределения определим требуемые характеристики: 1) средние затраты времени на изготовление одной детали:
2) доля деталей, на которые затрачивается до 24 мин.:
3) средние ошибки полученных характеристик определим по формулам собственно-случайного повторного отбора, так как доля выборки у нас незначительна и поправка на бесповторность отбора существенно не повлияет на результат:
Соответствующие дисперсии равны
Тогда
4) переход от средней (
Отсюда с вероятностью 0.954 можно указать границы для генеральных характеристик:
Задача 2. По данным задачи N1 определить предельные ошибки выборочных показателей с той же вероятностью при условии 20- процентного бесповторного отбора:
Задача 3. Сколько деталей необходимо отобрать из партии в 2000 штук в порядке бесповторного отбора, чтобы ошибка средних затрат времени на изготовление деталей не превышала 0,2 мин., а ошибка доли деталей, на изготовление которых тратится менее 24 мин. - 4%, с вероятностью 0,95.
Примечание: необходимые для расчетов дисперсии взяты из первой задачи. Оценка дисперсии при определении объема выборки является наиболее трудной проблемой планирования выборочного наблюдения.
ТЕСТЫ ВЫБОРОЧНЫЙ МЕТОД
1. Какой способ отбора может быть реализован только бесповторным методом? A. собственно-случайный; B. механический; C. серийный.
2. Средняя ошибка выборки: A. меньше предельной ошибки выборки; B. меньше или равна предельной ошибке выборки; C. больше или равна предельной ошибке выборки; D. больше предельной ошибки выборки.
3. Равная вероятность попадания в выборочную совокупность - A. основной принцип собственно-случайной выборки; B. основной принцип собственно-случайной выборки и комбинированной выборки с использованием собственно-случайного отбора; C. основной принцип любой выборки.
4. Метод основного массива и выборочный метод - это: A. практически один и тот же метод; B. разные методы.
5. Какая категория шире: A. несплошное наблюдение; B. выборочное наблюдение.
6. Какой метод отбора при прочих равных условиях обеспечивает меньшую необходимую численность выборки? A. повторный; B. бесповторный.
задачи для самостоятельного решения На основе выборочного метода из 30 банков ранее отобранных произведите отбор 10 банков, укажите способ отбора и рассчитайте по отобранным предприятиям: 1) среднюю стоимость капитала; 2) предельную ошибку этой средней и пределы, в которых можно полагать генеральную среднюю с вероятностью 0,954; 3) генеральную среднюю; 4) сравните результаты расчетов, полученных в пункте 1,2,3 и сформулируйте выводы. Тема 8 Ряды динамики и их анализ
Процесс развития, движения социально-экономических явлений во времени в статистике принято называть динамикой. Для ее отражения строятся ряды динамики (хронологические, временные), которые представляют собой ряды изменяющихся во времени значений статистического показателя, расположенных в хронологическом порядке. Составными элементами ряда динамики являются показатели уровней ряда и показатели времени (годы, кварталы, месяцы, сутки) или моменты (даты) времени. Уровни ряда обычно обозначаются через «y», моменты или периоды времени, к которым относятся - через «t». Существуют различные виды рядов динамики. Их можно классифицировать по следующим признакам: 1) В зависимости от способа выражения уровней ряды динамики подразделяются на ряды абсолютных, относительных и средних величин. 2) В зависимости от того выражают уровни ряда состояние явления на определенные моменты времени (на начало месяца, квартала, года и т.п.) или его величину за определенные интервалы времени (например, за сутки, месяц, год и т.п.), различают соответственно моментные и интервальные ряды динамики. Интервальные ряды динамики содержат данные о производстве продукции по месяцам или по годам, о товарообороте, о числе родившихся за период и т. п. Из различного характера интервальных и моментных рядов динамики вытекают некоторые особенности уровней соответствующих рядов. Уровни интервального ряда динамики абсолютных величин характеризуют собой суммарный итог какого-либо явления за определенный отрезок времени. Они зависят от продолжительности этого периода времени и поэтому их можно суммировать, как не содержащие повторного счета. Отдельные же уровни моментного ряда динамики абсолютных величин содержат элементы повторного счета, так как, например, часть вкладов населения, учтенных в 1990 г., существуют и в настоящее время, являясь единицами совокупности и в 1994 г. Все это делает бессмысленным суммирование уровней моментных рядов динамики. 3) В зависимости от расстояния между уровнями, ряды динамики подразделяются на ряды с равноотстоящими уровнями и неравноот-стоящими уровнями во времени. Ряды динамики следующих друг за другом периодов или следующих через определенные промежутки дат называется равноотстоящими (см. пример о числе вкладов в сберегательные банки РФ за 1990-1994 гг.). Если же в рядах даются прерывающиеся периоды или неравномерные промежутки между датами, то ряды называются неравноотстоящими 4) В зависимости от наличия основной тенденции изучаемого процесса ряды динамики подразделяются на стационарные и нестационарные. Если математическое ожидание значения признака и дисперсия (основные характеристики случайного процесса) - постоянны, не зависят от времени, то процесс считается стационарным, и ряды динамики также называются стационарными. Экономические процессы во времени обычно не являются стационарными, т.к. содержат основную тенденцию развития, но их можно преобразовать в стационарные путем исключения тенденций. Особое внимание следует обратить на условия сопоставимости данных, составляющих динамический ряд, данное условие решается либо в процессе сбора и обработки данных, либо путем их пересчета. Следовательно, прежде чем анализировать динамический ряд, на-до, исходя из цели исследования, убедится в сопоставимости уровней ряда и, если последняя отсутствует, добиться ее дополнительными рас-четами. Для того, чтобы привести уровни ряда динамики к сопоставимому виду, иногда приходится прибегать к приему, который носит на-звание смыкания рядов динамики. Под смыканием понимают объединение в один ряд (более длинный) двух или нескольких рядов динамики, уровни которых исчислены по разной методологии или в разных территориальных границах. Для осуществления смыкания необходимо, чтобы для одного из периодов (переходного) имелись данные, исчисленные по разной методологии (или в разных границах). Динамика объема продукции
Рассчитывая аналитические показатели ряда динамики, необходимо правильно выбирать базу для сравнения. Этому вопросу следует уделить особое внимание. Необходимо также разобраться в способах получения средних величин ряда: среднего уровня, среднего абсолютного прироста, среднего темпа роста и прироста. Следует помнить, что способ расчета среднего уровня ряда динамики зависит от его вида. При расчете среднего темпа роста необходимо использовать среднюю геометрическую. Анализ скорости и интенсивности развития явления во времени осуществляется с помощью статистических показателей, которые полу-чаются в результате сравнения уровней между собой Абсолютный прирост(Δу) характеризует размер увеличения (или уменьшения) уровня ряда за определенный промежуток времени. Он равен разности двух сравниваемых уровней и выражает абсолютную скорость роста: Δi = уi-yi-k (i=1,2,3,...,n) Если k=1, то уровень yi-1 является предыдущим для данного уровня, а абсолютные приросты изменения уровня будут цепными. Если же k постоянны для данного ряда, то абсолютные приросты будут базисными. Коэффициент роста или темп роста показывает во сколько раз данный уровень ряда больше базисного уровня (если этот коэффициент больше единицы) или какую часть базисного уровня составляет уровень текущего периода за некоторый промежуток времени (если он меньше единицы). В качестве базисного уровня в зависимости от цели исследования может приниматься какой-то постоянный для всех уровень (часто начальный уровень ряда), либо для каждого последующего предшествующий ему: В первом случае говорят о базисных темпах роста, во втором - о цепных темпах роста.
Наряду с темпом роста можно рассчитать показатель темпа прироста, характеризующий относительную скорость изменения уровня ряда в единицу времени. Темп прироста показывает, на какую долю (или процент) уровень данного периода или момента времени больше (или меньше) базисного уровня Тпр=Тр-100% Абсолютное значение одного процента прироста получается в результате деления абсолютного прироста по сравнению с предыдущим периодом на соответствующий темп роста, выраженный в процентах. Средний уровень моментного ряда динамики рассчитывается по средней хронологической. Для интервальных равноотстоящих рядов средний уровень находится по формуле средней арифметической простой и для неравноотстоящих рядов по средней арифметической взвешенной Средний абсолютный прирост:
Для расчета среднего темпа роста используем среднюю геометрическую:
Методы анализа основной тенденции (тренда) в рядах динамики Важной задачей статистики при анализе рядов динамики является определение основной тенденции развития, присущей тому или иному ряду динамики. Например, за колебаниями урожайности какой-либо сельскохозяйственной культуры в отдельные годы тенденция роста (уменьшения) урожайности может не просматриваться непосредственно, и поэтому должна быть выявлена статистическими методами. Методы анализа основной тенденции в рядах динамики разделяются на две основные группы: 1) сглаживание или механическое выравнивание отдельных членов ряда динамики с использованием фактических значений соседних уровней; 2) выравнивание с применением кривой, проведенной между конкретными уровнями таким образом, чтобы она отображала тенденцию, присущую ряду и одновременно освободила его от незначительных колебаний. Рассмотрим методы каждой группы. Метод укрупнения интервалов. Если рассматривать уровни экономических показателей за короткие промежутки времени, то в силу влияния различных факторов, действующих в разных направлениях, в рядах динамики наблюдается снижение и повышение этих уровней. Это мешает видеть основную тенденцию развития изучаемого явления. В этом случае для наглядного представления тренда применяется метод укрупнения интервалов, который основан на укрупнении периодов времени, к которым относятся уровни ряда. Например, ряд ежесуточного выпуска продукции заменяется рядом месячного выпуска продукции и т.д. Метод простой скользящей средней. Сглаживание ряда динамики с помощью скользящей средней заключается в том, что вычисляется средний уровень из определенного числа первых по порядку уровней ряда, затем средний уровень из такого же числа уровней, начиная со второго, далее - начиная с третьего и т.д. Таким образом, при расчетах среднего уровня как бы «скользят» по ряду динамики от его начала к концу, каждый раз отбрасывая один и уровень вначале и добавляя один следующий. Отсюда название - скользящая средняя. Каждое звено скользящей средней - это средней уровень за соответствующий период, который относится к середине выбранного периода, если число уровней ряда динамики нечетное. Нахождение скользящей средней по четному числу членов рядов динамики несколько сложнее, так как средняя может быть отнесена только к середине между двумя датами, находящимися в середине интервала сглаживания. Например, средняя, найденная для четырех членов, относится к середине между вторым и третьим, третьим и четвертым уровнями и так далее. Чтобы ликвидировать такой сдвиг, применяют так называемый способ центрирования. Центрирование заключается в нахождении средней из двух смежных скользящих средних для отнесения полученного уровня к определенной дате. При центрировании необходимо находить скользящие суммы, скользящие средние нецентрированные по этим суммам и средние из двух смежных нецентрированных скользящих средних. Покажем расчет 5-летней и 4-летней скользящей средней на примере данных
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 853; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.009 с.) |

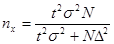 для среднего значения
для среднего значения
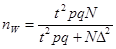 для доли
для доли
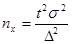 для среднего значения
для среднего значения
 для доли
для доли


 ;
; 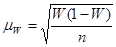


 (для средней)
(для средней) (для доли)
(для доли) ) к предельной (
) к предельной ( ) ошибке осуществляется по формуле
) ошибке осуществляется по формуле  (для всех видов выборки "t" -величина, связанная с вероятностью, с которой гарантируется результат). У нас Р = 0,954. Ей соответствует значение t = 2. Тогда имеем
(для всех видов выборки "t" -величина, связанная с вероятностью, с которой гарантируется результат). У нас Р = 0,954. Ей соответствует значение t = 2. Тогда имеем 

 или
или 
 или
или 




 - базисный
- базисный цепной
цепной
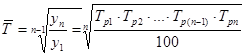 , 100%
, 100%


