
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Мода и медиана как разновидность средних величин в вариационных рядахСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Средние величины, о которых шла речь в данной главе, является своего рода отвлеченной, абстрактной величиной. Отвлекаясь от конкретных величин каждого варианта, эти числа отражают то общее, что присуще всей совокупности единиц. При этом может случиться, что величина средней не имеет равенства ни с одним из конкретных вариантов встречающихся в рассматриваемой совокупности вариантов. Например, среднее число членов семьи, равное 3,84, полученное на основе исчисления соответствующей совокупности данных, ничего общего с конкретным составом семьи не имеет, поскольку дробного числа членов семьи не может быть. Здесь в данном показателе средней величины состава семьи выражается некоторое центральное значение, около которого группируются реально существующие варианты. Кроме рассмотренных средних, когда определяется некая абстрактная величина, могут быть использованы величины конкретных вариантов имеющихся в рассматриваемой совокупности величин, величин занимающих определенное место в ранжированном ряду индивидуальных значений признака. Ранжировка признаков может быть построена в порядке возрастания или убывания индивидуальных значений признака. Такими величинами, чаще всего являются мода и медиана.
Таблица Мода - это наиболее часто встречающаяся в совокупности величина варианта. Эту величину означают символом Мо. Мода как величина в дискретном (прерывистом) ряду определяется следующим образом на примере выявления наибольшего процента мужчин носящих определенный размер обуви. Наглядно это можно представить следующей таблицей. Распределение числа мужчин по размеру используемой обуви В распределении мужчин по размеру обуви наибольшая часть мужчин (28%) относится к величине номера обуви в 41. Следовательно, мода Мо = 41, т.е. модой является 41-й размер обуви. Чтобы определить медиану, необходимо найти один из центральных вариантов рассматриваемой совокупности. В нашем примере центральным вариантом будет находиться в центре совокупности состоящей из 100 членов, т.е. 100: 2 = 50. Затем по накопленным частотам определяем величину 50-го члена ряда. В нашем примере он будет находиться между 41 и 69 накопленной частности (см. 3-ий столбец таблицы № 2), 50-ый член ряда имеет величину 41, т.е. Ме = 41-му размеру обуви. Вычисление моды (Мо) и медианы (Ме.) различно для дискретных и интервальных рядов. В дискретных рядах мода определяется по наибольшей частоте. Для определения медианы вычисляются накопленные частоты, медианным будет тот вариант, накопленная частота которого первой превысит половину всех частот. Для интервальных вариационных рядов расчет моды и медианы требует применения специальных формул:
Определим моду и медиану по следующему ряду распределения:
Определим моду и медиану:
В практике мода и медиана часто используются вместо средней арифметической или наряду с ней. Так, фиксируя средние цены на оптовых рынках, записывают наиболее часто встречающуюся цену каждого продукта, т.е. определяют моду цены. Тем не менее наилучшей характеристикой величины варианта служит средняя арифметическая, которая имеет ряд существенных преимуществ, главное из которых, точное отражение суммы всех значений признака, использующихся для решения соответствующих практических задач Специальные средние Средние прогрессивные – используются для расчета прогрессивных нормативов выработки или расхода ресурсов (сырье, материалов и др.) Средняя прогрессивная представляет собой математическую среднюю арифметическую, рассчитанную по Процедура расчета: 1. рассчитывается средне арифметическое для всей совокупности. Определяют Задача: рассчитать прогрессивную норму выработки продавца для организации материального стимулирования. Наблюдения за производительностью показала, что выработка за месяц составила:
Средняя хронологическая - используется для осреднения значений привязанных к моменту времени:
средний остаток материалов на складе: 1.04.2001 -110 тыс. руб 1,05.2001 -120 тыс руб. 1,06,2001 -100 тыс. руб 1.07.2001 -110 тыс. руб
средние остатки товарно - материальных ценностей используется при расчете коэффициента оборачиваемости. По правилам средней хронологической рассчитываются: средний срок хранения вклада, средний остаток работающих активов, средний остаток оплаченных ресурсов и кредитов, оплачиваемых в банке.
Вопросы для самопроверки
ПРАКТИЧЕСКАЯ РАБОТА ТЕМА 4 Задача 1. Объем продаж компании Samsung в странах СНГ в I полугодии 1996г. составил 250 млн. долл. В целом же за год компания планировала реализовать товаров на 600 млн. долл. Вычислите относительный показатель плана на II полугодие. Задача 2. . Предприятие планировало увеличить выпуск продукции в 1997г. по сравнению с 1996г. на 18%. Фактический же объем продукции составил 112,3% от прошлогоднего уровня. Определите относительный показатель реализации плана Задача 3. Имеются следующие данные о производстве бумаги в РФ
Вычислите относительные показатели динамики с переменной и постоянной базой сравнения. Проверьте их взаимосвязь Задача 4. Добыча нефти и угля в РФ во II квартале 1996г. характеризуется следующими данными:
Теплота сгорания нефти равна 45,0 мДж/кг, угля - 26,8 мДж/кг. Сделайте пересчет в условное топливо (29,3 мДж/кг) и проведите анализ изменения совокупной добычи этих ресурсов.
.Задача 5 В апреле 1996г. прожиточный минимум для трудоспособного населения составил 419,0 тыс. руб. в месяц на человека, для пенсионеров - 262,5 тыс. руб., для детей - 376,1 тыс. руб. Сделайте выводы о соотношении этих величин, используя относительные показатели сравнения. Задача 6 .: Известно распределение работников предприятия по возрасту:
Определите средний возраст работника, рассчитайте моду и медиану
Задача 7 По следующим данным определите, в каком семестре уровень успеваемости студентов потока был выше:
Задача 8. Имеются следующие данные о дневной реализации помидоров на рынках города:
Вычислите среднюю цену 1 кг помидоров в целом по всем рынкам города Задача.9.. По трем районам города имеются следующие данные (на конец года
Задача.10 По результатам обследования сельхозпредприятий области получены следующие данные
Определите средний надой молока на одну корову и среднюю жирность молока.
Тесты
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 540; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.166.34 (0.009 с.) |

 где
где - нижняя граница модального интервала (модальным называется имеющий наибольшую частоту);
- нижняя граница модального интервала (модальным называется имеющий наибольшую частоту); - величина модального интервала;
- величина модального интервала; - частота модального интервала;
- частота модального интервала; - частота интервала, предшествующего модальному;
- частота интервала, предшествующего модальному; частота интервала, следующего за модальным
частота интервала, следующего за модальным , где
, где - накопленная частота интервала, предшествующего медианному;
- накопленная частота интервала, предшествующего медианному; частота медианною интервала.
частота медианною интервала.
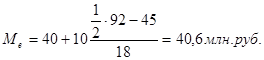
 при определении норм расхода и при определении норм выработки
при определении норм расхода и при определении норм выработки  .
.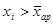 и по выделенным значениям снова рассчитывают среднюю арифметическую, она и будет средней прогрессивной.
и по выделенным значениям снова рассчитывают среднюю арифметическую, она и будет средней прогрессивной.
 , выделим
, выделим 





