
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Блок 6. Абсолютные и относительные величины, средние величиныСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Абсолютные величины – это численности единиц и суммы по группам, а также по совокупности в целом, которые являются результатом сводки и группировки данных. Абсолютные величины – именованные числа с определенной размерностью и единицей измерения. По способу выражения размеров изучаемых явлений абсолютные величины разделяются на индивидуальные и суммарные. Индивидуальные характеризуют размеры количественных признаков у отдельных единиц совокупности, а суммарные – совокупности в целом. Для абсолютных величин важным является вопрос выбора единицы измерения. Выделяют три типа единиц измерения: натуральные, денежные и трудовые. Натуральные величины могут быть составными. Например, работа транспорта выражается в тонно-километрах или в пассажиро-километрах, а затраты труда в человеко-часах или в человеко-днях. Применяются также условно-натуральные единицы измерения, которые получают приведением различных натуральных единиц к одной, принятой за базу для приведения к общему знаменателю. Это может быть условная банка (емкость 353,4 см3) в консервной промышленности или условное топливо в топливной промышленности. Абсолютные величины получают не всегда суммированием, они могут быть получены путем сложных расчетов. Расчетным путем могут быть получены недостающие показатели с использованием балансовых связей. Например, Зн +П = Р + Зк, Зн = Р + Зк – П, где Зн и Зк – запасы на начало и конец периода, П – поступления, Р – реализация в течение периода. Относительные величины – это производные обобщающие показатели, представленные средними и относительными статистическими величинами. Анализ предполагает сопоставление величин тех или иных показателей, в результате такого сопоставления получают качественную оценку. Относительные величины – частное от деления двух величин, где числитель – это показатель, отражающий изучаемое явление, а знаменатель – показатель, с которым производится сравнение – база сравнения. База сравнения выступает своеобразным измерителем. В зависимости от того, какое значение имеет база сравнения результат сопоставления может быть выражен в виде кратных отношений - коэффициентов, процентных отношений, промилле (расчеты на 1000), децимилле (на 10000) Относительные величины подразделяются на следующие виды: структуры, динамики, сравнения, координации, интенсивности, выполнения планового задания, выполнения плана. Расчеты этих показателей производится путем сопоставления следующих показателей:
Разновидностью относительных величин являются средние величины. Нахождение средних величин для совокупностей – один из наиболее распространенных способов обобщения. Бельгийский статистик А. Кетле считал выделение средних величин основным приемом статистического анализа, сами средние величины не просто мерой математического измерения, а объективной реальностью. А. Кетле выдвинул теорию «среднего человека» как некий образец, наделенный всеми качествами в среднем размере. В 19 веке эта механистическая теория была популярна и стала предметом многих научных дискуссий. Средняя величина – абстрагируется от разнообразия отдельных единиц совокупности и уходит от структуры явления. Но такое абстрагирование находится в диалектическом единстве массового и индивидуального и является необходимым приемом статистического анализа. В статистике средние величины имеют ключевое значение, являясь сводными обобщающими показателями. Средние величины – это обобщающая или типическая характеристика исследуемого количественно варьирующего признака на определенный момент времени в расчете на единицу совокупности. Отдельная средняя величина характеризует изучаемое явление с одной стороны, для всестороннего изучения явления требуется исследование по возможно большему числу существенных признаков. Только в этом случае можно составить объективное представление о явлении в целом и отдельных его частях. Различные средние величины можно представить в виде формулы степенной средней:
при z= 1- средняя арифметическая; z= 2 – средняя квадратическая; z= 0 - средняя геометрическая; z= -1- средняя гармоническая;
Признак, по которому определяется средняя, называется осредняемым признаком (͞х), индивидуальные значения признака – варианты (х1, х2, х3 …..хn), а повторяемость вариантов - частота (f). Средняя арифметическая – наиболее часто применяемая средняя величина: ͞х = Например, группа туристов из десяти человек по числу заграничных туров распределилась следующим образом: 4, 2, 5, 2, 3, 1, 3, 6, 2, 3. Среднее число туров на одного человека в группе:
͞х =
Если туристов объединить в группы по числу туров, то их среднее значение можно подсчитать как среднюю арифметическую взвешенную (табл.3):
Таблица 3 Распределение группы туристов по числу заграничных туров, в которых они побывали
Часто возникает необходимость вычисления средних величин для интервальных рядов. Например, необходимо рассчитать средний возраст туристов различных возрастных групп (табл. 4). Таблица 4 Распределение групп туристов по возрасту
Средний возраст группы туристов составляет:
Средняя гармоническая – это величина обратная средней арифметической, рассчитывается из обратных значений признака: ͞xh=
применяется, когда отсутствуют частоты по исходным данным, но они входят сомножителем в один из имеющихся показателей (табл. 5). Таблица 5
Известны цены и общая сумма выручки за один и тот же товар в разных магазинах. Для определения физического объема реализации необходимо сумму реализации в каждом магазине разделить на цены. Среднюю цену за товар по группе магазинов можно рассчитать по средней гармонической взвешенной:
Свойства средней арифметической Средняя арифметическая располагает рядом свойств, которые значительно упрощают расчеты на практике: Свойство 1. Если все веса (f) увеличить или уменьшить в одинаковое число раз (а), то величина средней не изменится:
Свойство 2. Если каждую варианту (x) увеличить или уменьшить на одну и туже величину А, то средняя увеличится или уменьшится на ту же варианта отнять или прибавить произвольное постоянное число А, то средняя уменьшится или увеличится на то же число А:
Свойство 3. Если каждую варианту (х) увеличить или уменьшить в одно и то же число раз (i), то средняя увеличится или уменьшится в то же число раз:
Свойство 4.. Сумма отклонений отдельных вариантов от средней, взвешенных их частотами равна нулю:
Последнее свойство проверим на примере, когда турагентство организует поездки с различной дальностью:
Блок 7. Структурные средние Структурные средние характеризуют структуру рядов распределения. К структурным средним относятся мода и медиана. Мода (Мо) – значение признака, которое наиболее часто встречается в изучаемой совокупности. В дискретном ряду мода – это варианта с наибольшей частотой. В интервальном вариационном ряду мода определяется по формуле:
где Модальный интервал – интервал, имеющий наибольшую частоту (частость). Например, среднедушевые доходы городского населения распределись следующим образом (табл.6). Таблица 6
Рассчитаем модальное значение среднедушевых доходов населения города:
Наиболее частое значение среднедушевых доходов – 13125 рублей. Медиана (Ме) - это величина, которая делит численность упорядоченного вариационного ряда на две равные части – одна часть меньше, чем средний вариант, а другая больше. Для ранжированного ряда с нечетным числом членов медианой является варианта, расположенная в центре ряда. Например, стажи работы специалистов в туристской фирме – 1,2, 2, 3, 3, 4, 5 лет – медианой является четвертая варианта – 3 года. Для ранжированного ряда с четным числом членов ряда медианой будет средняя арифметическая из двух смежных вариант, находящихся в середине ряда. Например, сотрудники туристской фирмы имеют следующие стажи работы по специальности: 2, 2, 3, 4, 4, 6 лет – медианой является значение, равное: (3+4):2=3,5 года. Чтобы определить медиану, необходимо найти ее порядковый номер, а затем по накопленным частотам (частостям) определить величину варианта, обладающего таким номером. Для определения медианного значения в интервальном ряду используется следующая формула:
где, Медианный интервал – интервал, в котором находится порядковый номер медианы. Для его определения подсчитывают суммы накопленных частот (частостей) до числа, превышающего половину объема совокупности. Медианное значение среднедушевых доходов населения города составит:
Аналогичным образом могут быть рассчитаны четверти общего ряда – квартили, десятые доли – децили, сотые доли – процентили. Блок 8. Показатели вариации Различие индивидуальных значений признака внутри изучаемой совокупности называется вариацией признака. Колеблемость отдельных значений характеризуют показатели вариации. Различают вариацию признака случайную и систематическую. Анализ вариации позволяет оценить ее характер и определить насколько однородной является изучаемая совокупность и насколько характерной является ее средняя величина для данной совокупности. Выделяют абсолютные и средние показатели вариации. Наиболее простой – размах вариации (R) – разность между наибольшим и наименьшим значением признака в распределении: R= Для получения обобщенной характеристики отклонений от средней рассчитывают среднее линейное отклонение На практике вариацию чаще оценивают с помощью показателя дисперсии Если из дисперсии извлечь корень квадратный, то получится еще один показатель вариации – среднее квадратическое отклонение:
Коэффициент осцилляции характеризует относительную колеблемость крайних значений признака вокруг средней:
Относительное линейное отклонение характеризует долю усредненного значения абсолютных отклонений от средней величины:
Наиболее распространенный показатель колеблемости, который дает обобщающую характеристику – коэффициент вариации:
Рассмотрим пример, где оценивается вариация стажа работы по специальности работников двух турфирм: 1-я 2-я 1 4 2 4 3 5 4 5 4 5 9 7 10 7 12 7 45 лет 45 лет Проведем предварительные расчеты:
Сопоставим показатели вариации стажа работников у двух турфирм. 1-я фирма 2-я фирма
При одинаковых средних величинах стажа работников фирм вариация признака в первой фирме в три раза выше, чем в первой. Преобразование формулы среднего квадратического отклонения приводит ее к виду Дисперсия альтернативного признака характеризует вариацию альтернативных признаков. Альтернативными признаками являются признаки, которыми обладают одни единицы изучаемой совокупности и не обладают другие. Например, в фирме работают мужчины и женщины, доля мужчин (р) и доля женщин (q) образуют целый коллектив сотрудников фирмы: p +q = 1. Средняя величина для альтернативных признаков равна Правило сложения дисперсий. Если совокупность варьирующих элементов подразделить на несколько групп, то можно выделить: общую дисперсию ( Общая дисперсия характеризует колеблемость признака во всей изучаемой совокупности и рассчитывается по формуле:
Внутригрупповая дисперсия характеризует колеблемость признака внутри группы и рассчитывается по формуле:
Средняя из внутригрупповых характеризует внутригрупповую колеблемость вокруг внутригрупповых средних и рассчитывается как средняя величина из внутригрупповых дисперсий:
Межгрупповая дисперсия показывает вариацию групповых средних вокруг общей средней, измеряет вариацию изучаемого признака под влиянием признака - фактора (группировочного признака) и рассчитывается по формуле:
Между всеми приведенными дисперсиями существует взаимосвязь, которая называется правилом сложения дисперсий – общая дисперсия равна сумме средней из внутригрупповых дисперсий и межгрупповой дисперсии:
Логика этого правила следующая: общая дисперсия, возникающая под влиянием всех факторов, должна быть равна сумме дисперсий, возникающих под влиянием всех прочих факторов, и дисперсии возникающей за счет фактора группировки. Зная два вида дисперсий, всегда можно определить или проверить правильность расчета третьего вида дисперсии. Например, имеются данные по среднедневной выработке сотрудников фирмы с различным стажем работы:
В статистике применяется показатель, представляющий собой долю межгрупповой дисперсии в общей дисперсии, который показывает, какая часть общей вариации изучаемого признака обусловлена вариацией группировочного признака. Это коэффициент детерминации, рассчитываемый по формуле: Если извлечь корень квадратный из коэффициента детерминации, получаем новый показатель, который носит название корреляционное отношение:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 647; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.05 с.) |


 =
=  ,
,  =
=  .
.

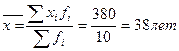
 (простая); ͞ xh =
(простая); ͞ xh =  (взвешенная)
(взвешенная)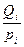

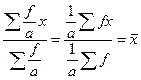 .
.

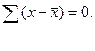
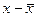


 км.;
км.; 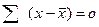 .
.
 нижняя граница модального интервала;
нижняя граница модального интервала;  величина модального интервала;
величина модального интервала;  частоты модального, домодального и послемодального интервалов.
частоты модального, домодального и послемодального интервалов. тыс. руб.
тыс. руб.

 нижняя граница медианного интервала;
нижняя граница медианного интервала;  - величина медианного интервала;
- величина медианного интервала; 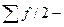 полусумма частот ряда;
полусумма частот ряда; 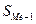 - сумма накопленных частот, предшествующих медианному интервалу;
- сумма накопленных частот, предшествующих медианному интервалу;  - частота медианного интервала.
- частота медианного интервала. тыс. руб.
тыс. руб. .
.
 для несгруппированных данных и для вариационного ряда
для несгруппированных данных и для вариационного ряда  показатель учитывается без знака этих отклонений.
показатель учитывается без знака этих отклонений. в варианте без частот и
в варианте без частот и 
 в варианте без частот и
в варианте без частот и  в варианте с частотами.
в варианте с частотами.




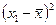


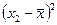




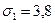



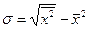 , что делает ее удобнее для практических расчетов. Этот показатель широко применяется для расчетов показателей вариации в различных отраслях знания и техники. Среднее квадратическое отклонение показывает, на сколько в среднем отклоняются конкретные варианты от среднего их значения.
, что делает ее удобнее для практических расчетов. Этот показатель широко применяется для расчетов показателей вариации в различных отраслях знания и техники. Среднее квадратическое отклонение показывает, на сколько в среднем отклоняются конкретные варианты от среднего их значения. а дисперсия
а дисперсия  . Если на фирме работает 15 мужчин и 20 женщин, то р=
. Если на фирме работает 15 мужчин и 20 женщин, то р= 
 , следовательно дисперсия альтернативного признака
, следовательно дисперсия альтернативного признака 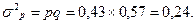 Максимальное значение дисперсии альтернативного признака равно 0,25, оно получается при р=0,5.
Максимальное значение дисперсии альтернативного признака равно 0,25, оно получается при р=0,5.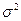 ), внутригрупповую дисперсию (
), внутригрупповую дисперсию ( ), среднюю из внутригрупповых дисперсий (
), среднюю из внутригрупповых дисперсий ( ), межгрупповую дисперсию (
), межгрупповую дисперсию ( ).
). , где
, где 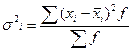 , где
, где 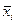 - групповая средняя.
- групповая средняя.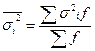 , где
, где  - дисперсии отдельных групп, а f - численность отдельных групп.
- дисперсии отдельных групп, а f - численность отдельных групп. , где
, где 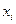 и
и  - средние и численности по отдельным группам.
- средние и численности по отдельным группам.
 .
.

 т. рублей
т. рублей
 , следовательно:
, следовательно:  .
. .
. .
.


