
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модуль 5. Статистические методы прогнозирования процессовСодержание книги
Поиск на нашем сайте
Блок 12. Ряды динамики. Исследование основных тенденций развития явлений Все социально-экономические явления развиваются во времени. Динамизм явлений является результатом взаимодействия многих причин и факторов. Изучение динамики развития явлений преследует цель – выявление и измерение тенденций и закономерностей их развития. Для того, чтобы можно было проанализировать явления в развитии, необходимо построить ряды динамики. Рядами динамики называются статистические данные, отображающие развитие явления во времени. Ряды динамики имеют два основных элемента: 1. уровни, характеризующие величину признака; 2. периоды, к которым относятся уровни. Ряды динамики могут быть: моментными, когда состояние явления фиксируется на какой-то момент и интервальными, когда явление отражается за отдельные периоды времени. С помощью рядов динамики осуществляется изучение закономерностей развития социально-экономических явлений по следующим направлениям: 1) характеристика уровней развития явлений во времени; 2) измерение динамики развития явлений с помощью системы статистических показателей; 3) выявление и количественная оценка основных тенденций развития явлений (тренда); 4) изучение периодических колебаний в развитии явлений; 5) экстраполяция и прогнозирование развития явлений. Основным условием правильного построения ряда динамики является сопоставимость его элементов. Ряды динамики формируются в результате сводки и обработки материалов периодических наблюдений. Повторяющиеся во времени значения отдельных показателей систематизируются в хронологической последовательности. При этом ряды динамики охватывают отдельные периоды времени, когда изучаемые явления могут находиться в различных условиях, которые могут привести к несопоставимости отчетных данных с данными других периодов. В этих случаях необходимо приведение всех составляющих элементов к сопоставимому виду. Для этого проводится анализ причин, приведших к несопоставимости полученной информации и применяется соответствующая обработка, позволяющая привести показатели к сопоставимому виду. Причины несопоставимости показателей в рядах динамики могут быть различными. Это может быть разновеликость показателей времени, неоднородность состава изучаемых совокупностей во времени, изменение методики первичного учета и сводки исходной информации, различия применяемых единиц измерения, ценовые изменения и т.д. Данные могут быть несопоставимыми по кругу охватываемых объектов. Например, в городе сначала было 14 гостиниц, затем в строй действующих в 2002 г. было введено еще две. Изучение динамики валовой продукции (услуг) гостиниц во времени стали несопоставимыми. Привести к сопоставимости динамического ряда можно следующим образом:
Для того, чтобы динамический ряд сделать сопоставимым 2002 г., когда были введены в стой действующих еще две гостиницы, был принят за 100%. Уровни динамического ряда могут быть рассчитаны различными способами. Например, часть показателей зафиксированы на определенную дату, а другая часть рассчитана как среднегодовая численность. В этом случае необходимо провести перерасчет данных и привести к их к одному показателю. Характеристики динамики Для количественной оценки динамики развития явлений используются статистические показатели динамики: абсолютные приросты, темпы роста и прироста, которые дают характеристику направления и размер изменений явления во времени. Рассмотрим условный пример с потоками туристов в регион в течение ряда лет:
Средний уровень динамики для интервальных рядов представим как Для моментных рядов фиксируется состояние явления на определенный момент, это могут быть данные на начало или конец какого-либо периода (например, по состоянию на 1 января текущего года). Средний уровень здесь определяется как средняя арифметическая из двух этих показателей. Например, численность работников турфирмы на 1 января.
60 человек на 1 января 2003 г. – это одновременно численность работников фирмы на 31 декабря 2002 г. Поэтому средняя численность работников: за 2003 г. за 2005г. Средняя численность за период составила Средний уровень моментного ряда рассчитывается также по средней хронологической:
Например, имеются данные о числе гостей в отеле по состоянию на начало квартала в течение 2005 года.
Средняя численность гостей в течение года:
В динамических рядах определяют вариацию динамики по формулам:
С помощью простейших показателей определим направление и размер изменений уровней во времени по данным потоков туристов в регионе в течение ряда лет:
Исследование тенденций развития явлений Изменение уровней рядов динамики связано с влиянием на изучаемое явление множества факторов, которые различны по силе воздействия, направлению и времени их действия. Постоянно действующие факторы оказывают на явление определяющее воздействие и формируют в рядах динамики основное направление развитие – тренд. Воздействие других факторов, как правило, периодическое и вызывает колебания уровней рядов динамики. Определенное воздействие на динамику развития явления могут оказывать отдельные случайные (спорадические) факторы. Воздействие постоянных, периодических и разовых причин на уровни динамики развития явления вызывает необходимость изучения этих факторов для определения тренда, периодических колебаний и случайных отклонений. Простейший способ обработки динамического ряда с целью выявления тенденции его развития заключается в укрупнении интервалов времени. Предположим, имеются данные о количестве гостей в отеле по месяцам в течение года:
Укрупнив интервалы, устранили случайные колебания и проявили основную тенденцию сезонных колебаний в потоке гостей в течение года. Сглаживание способом скользящей средней. Суть этого способа заключается в замене фактических уровней рядом подвижных (скользящих) средних, которые рассчитываются для последовательно подвижных интервалов и относятся к середине каждого из них. Сглаживание этим способом можно производить по любому числу членов ряда. Если осуществляется сглаживание ряда динамики с интервалом из 5 членов, то в этом случае необходимо последовательно суммировать по 5 членов и результаты делить на 5. Например, поток туристов в страну в течение 10 лет составил:
Недостатком сглаживания ряда способом скользящей средней является то, что Выравнивание по аналитическим формулам. Этот способ обработки динамических рядов является более совершенным по сравнению с вышеприведенными способами. Способ предполагает подбор наиболее подходящей функции, для отражения тенденции развития изучаемого явления. Задача выравнивания здесь сводится к определению вида функции, отысканию ее параметров по эмпирическим данным и расчету теоретических уровней по найденной формуле. К наиболее простым формулам, отражающим тенденции развития относятся: 1) прямая вида 2) парабола второго порядка 3) показательная функция 4) гипербола Выравнивание по прямой. Как правило, используется в тех случаях, когда абсолютные приросты относительно постоянны, т.е. когда уровни изменяются приблизительно в рамках арифметической прогрессии. Параметры a и b искомой прямой находятся решением системы нормальных уравнений:
где y - уровни эмпирического ряда, n – количество уровней ряда, t- время Эту систему можно упростить, если отсчет моментов времени ведется от середины ряда. При нечетном числе уровней ряда средняя точка принимается за 0, тогда предшествующие периоды обозначаются: -1,-2,-3 и т.д., а последующие за средним: +1,+2,+3 и т.д. В сумме t должно сводиться к 0. При четном числе уровней ряда два серединных момента времени принимаются за -1 и +1 и все остальные соответственно обозначаются через два интервала:-5, -3, -1, +1, +3, +5, В этом случае
b Рассмотрим условный пример с потоками туристов в регион в течение 5 лет:
Определяем параметры: Тогда уравнение теоретической прямой будет иметь вид: Выравнивание по параболе 2-го порядка. Выравнивание по параболе 2-го порядка
При
Произведем выравнивание динамического ряда объема услуг фирмы за 6 лет параболой 2-го порядка:
Полученные суммы по столбцам подставим в систему уравнений:
70 а1 = 435,4 70 а0 +1414 а2 = 4155,6 Решив уравнение, находим: а0 = 53,73; а1 = 6,22; а2 = 0,28. Отсюда искомое уравнение параболы 2-го порядка уt= 53,73+6,22t+0,28t2. На основе этого уравнения рассчитаем выравненные уровни, подставив соответствующие значения t и занесем их в последнюю графу таблицы. Выравнивание по показательной функции. В основном производится, когда динамический ряд отражает развитие процесса в геометрической прогрессии. Уравнение показательной функции
Отсюда Произведем выравнивание динамического ряда продаж турфирмой туристских путевок в течение 7 лет:
lg a=
следовательно, Подставляем в формулу значения t, найдем логарифмы Для 2000 г. lgy=2,0707+0,0121(-3)=2,0344 или Выравненные уровни близки к эмпирическим уровням, значит показательная функция подходит для отражения тренда.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 363; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.104.30 (0.012 с.) |

 где n – число уровней.
где n – число уровней. 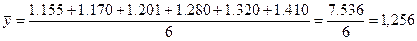 млн. человек.
млн. человек. чел. за 2004 г.
чел. за 2004 г.  =78 чел.
=78 чел. чел. за 2006 г.
чел. за 2006 г. 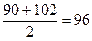 чел.
чел. чел.
чел.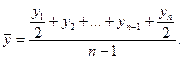
 чел.
чел.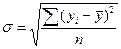
 и
и 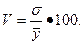






 члена с одного и другого конца (n- число членов, из которых рассчитываются скользящие средние). В нашем случае это по
члена с одного и другого конца (n- число членов, из которых рассчитываются скользящие средние). В нашем случае это по  с каждой стороны.
с каждой стороны. , где
, где  -теоретический уровень, t – время, a и b – параметры прямой.
-теоретический уровень, t – время, a и b – параметры прямой.

 .
.

 ,
, и система уравнений принимает вид:
и система уравнений принимает вид:

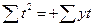 , тогда
, тогда 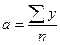 ,
,  .
.



 , b=
, b= 
 сводится к нахождению параметров a,b,c из системы нормальных уравнений:
сводится к нахождению параметров a,b,c из системы нормальных уравнений:


 .
.

 .
. 6 а0 + 70 а2 = 342
6 а0 + 70 а2 = 342 . Логарифм показательной функции представляет собой уравнение прямой
. Логарифм показательной функции представляет собой уравнение прямой  Заменив уровни ряда их логарифмами, параметры a и b можно определить через их логарифмы. Система уравнений подобна системе уравнений при выравнивании по прямой.
Заменив уровни ряда их логарифмами, параметры a и b можно определить через их логарифмы. Система уравнений подобна системе уравнений при выравнивании по прямой. 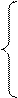


 Если
Если 

 и
и  .
.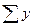

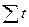


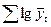


 ,
, или
или  .
. .
.


