
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вопрос 3. Использование относительных и средних величин в АХДСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Экономические явления и процессы, изучаемые в АХД, выражаются в абсолютных и относительных показателях. Абсолютные показатели отражают количественные размеры явления в единицах меры, веса, объема, продолжительности, площади, стоимости и т.д. безотносительно к размеру других явлений, а относительные – соотношение величины изучаемого явления и величины какого-либо другого явления или величины этого явления, но взятой за другой период или по другому объекту. Относительные показатели получают в результате деления одной величины на другую, которая принимается за базу сравнения. Это могут быть данные плана, базисного года, другого предприятия, среднеотраслевые и т.д. Относительные величины выражаются в форме коэффициентов (при базе 1) или процентов (при базе 100). Виды относительных величин: Относительная величина пространственного сравнения получается в результате сопоставления уровней показателей, относящихся к различным объектам, взятым за один и тот же период или на один момент времени. Относительная величина планового задания представляет собой отношение планового уровня показателя текущего года к фактическому его уровню в прошлом году или к среднему за три-пять предыдущих лет. Относительная величина выполнения плана – отношение между фактическим и плановым уровнями показателя отчетного периода, выраженное в процентах. Относительные величины динамики используют для характеристики изменения показателей за какой-либо промежуток времени и определяют путем деления величины показателя текущего периода на его уровень в предыдущем периоде (месяце, квартале, году). Называются они темпами роста (прироста) и выражаются обычно в процентах или коэффициентах. Относительные величины динамики могут быть базисными (каждый следующий уровень динамического ряда сравнивается с базисным годом) и цепными (уровень показателя следующего года относится к предыдущему). Показатель структуры – это относительная доля (удельный вес) части в общем, выраженная в процентах или коэффициентах. Например, удельный вес посевов зерновых культур в общей посевной площади, удельный вес рабочих в общем количестве работников предприятия, удельный вес собственного капитала в формировании активов предприятия. Относительные величины координации представляют собой соотношение частей целого между собой, например активной и пассивной частей основных производственных фондов, силовых и рабочих машин, собственного и заемного капитала и т.д. Относительные величины интенсивности характеризуют степень распространенности, развития какого-либо явления в соответствующей среде, например степень заболеваемости персонала, процент рабочих высшей квалификации и т.д. Относительные величины эффективности – это соотношение эффекта с ресурсами или затратами, например размер прибыли на рубль затрат, на одного рабочего, на рубль выручки, на рубль вложенного капитала и т.д. Наряду с абсолютными и относительными показателями применяются средние величины для обобщенной количественной характеристики совокупности однородных явлений по какому-либо признаку. Например, средняя зарплата рабочих используется для обобщающей характеристики уровня оплаты труда изучаемой совокупности рабочих. В АХД применяют разные типы средних величин (табл. 4) Таблица 4 –Виды и порядок расчета средних величин
При использовании средних величин в АХД следует учитывать, что они дают обобщенную характеристику явлений, основываясь на массовых данных.
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 597; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.006 с.) |

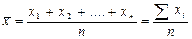 ,
где х1, х2,…., хп - варианты показателя;
п - число вариантов
,
где х1, х2,…., хп - варианты показателя;
п - число вариантов
 где х1, х2,..., хп - варианты показателя,
f1, f2,...,f n - общая численность каждого варианта;
∑ fi - общее число единиц совокупности
где х1, х2,..., хп - варианты показателя,
f1, f2,...,f n - общая численность каждого варианта;
∑ fi - общее число единиц совокупности
 где п - число вариантов (коэффициентов роста), которое будет на единицу меньше числа членов динамического ряда
где п - число вариантов (коэффициентов роста), которое будет на единицу меньше числа членов динамического ряда
 где х1, х2,.., хп - уровень показателя на определенную дату; п - число дат
где х1, х2,.., хп - уровень показателя на определенную дату; п - число дат




